2021.5.16模拟赛赛后总结
赛后总结
前言
不得不说这次比赛质量终于高了起来。
昨天晚上还在吐槽杰哥出题水平,没想到今天就被爆干了
T1
简要题意:有一些字符串,需要改成另一个给定的字符串,过程中不允许字符串重复冲突,问最少改几次。
根据题目我们可以得知,这一些字符串只会有三种情况:
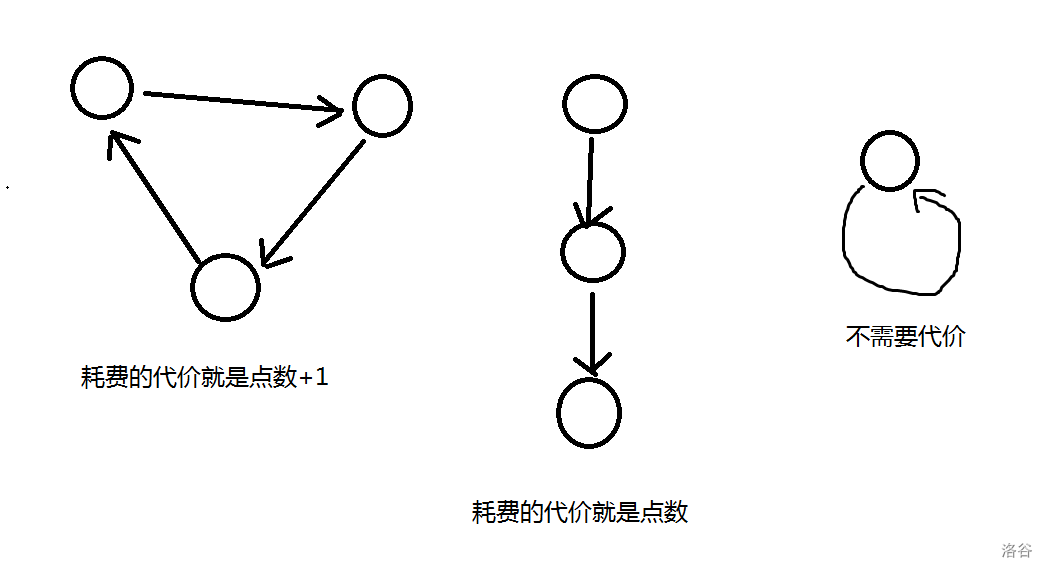
所以我们要做的就是判定他是一个环,还是一条链,还是一个单节点
单个的节点很好处理,直接不需要更改;
环形判到最后的时候,返回一个 \(2\),
链形判到最后,返回一个 \(1\),
哈希加DFS:
//#define LawrenceSivan
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
#define re register
const int maxn=1e5+5;
#define INF 0x3f3f3f3f
typedef unsigned long long ull;
const ull base=131;
const int prime=233317;
ull Hash(string a){
int len=a.size();
ull ans=0;
for(re int i=0;i<len;i++){
ans=ans*base+(ull)a[i];
}
return ans;
}
ull hasha[maxn],hashb[maxn];
int n;
int cnt,dfn[maxn];
int all_ex,ans;
map<ull, int> q;
map<ull, int>::iterator it;
bool vis[maxn];
int dfs(int x){
vis[x]=true;
dfn[x]=cnt;
it=q.find(hashb[x]);
if(it==q.end())return 1;
int n=it->second;
if(!vis[n])return dfs(n)+1;
else {
if(dfn[n]==dfn[x])return 2;
else return 1;
}
}
inline int read(){
int x=0,f=1;char ch=getchar();
while(!isdigit(ch)){if(ch=='-')f=-1;ch=getchar();}
while(isdigit(ch)){x=x*10+(ch^48);ch=getchar();}
return x*f;
}
int main(){
#ifdef LawrenceSivan
freopen("files.in","r",stdin);
freopen("files.out","w",stdout);
#endif
n=read();
for(re int i=1;i<=n;i++){
string a,b;
cin>>a>>b;
if(a==b)vis[i]=true;
else{
hasha[i]=Hash(a);
hashb[i]=Hash(b);
q[hasha[i]]=i;
}
}
for (int i=1;i<=n;++i){
if(!vis[i])cnt++,ans+=dfs(i);
}
printf("%d\n",ans);
return 0;
}
/*
5
fc diff
dm gen
chk fc
spj spj
diff chk
*/
/*
8
1 5
2 6
3 8
4 2
5 1
6 4
7 3
8 9
*/
T2
待补充:
T3
求 \(n\) 个矩形的面积并。
我们可以用一根竖直的或者水平的线扫过坐标系,这样的话我们可以发现,面积的变化只会出现在两端线段的位置上。(这里我倾向于竖直的)

(图片是 @Gu_Pigeon 的)
也就是说,我们只需要记录一个矩形的左右两条竖直的边,也就是把一个矩形分成 \(2 \times n\) 段,每一段在扫描线上覆盖的长度乘上这一段的宽度就是这一段的矩形面积,把所有的矩形面积都加起来就可以获得面积并了。
。在本题中,题目会给出左下角和右上角的坐标,于是我们可以记录左右两条边。分别用一个四元组来记录:
\((x_1,y_1,y_2,1)\)
\((x_2,y_1,y_2,-1)\)
struct Line{
ll x,low,high;
int mark;
bool operator < (const Line &a)const{
return x < a.x;
}
}line[maxn<<1];
其中我们假设 \(x_1<x_2,y_1<y_2\) ,并且用 \(1/-1\)
来表示这个边是左边还是右边。
之后我们可以对这些四元组按照 \(x\) 递增排序。
之后要对这些线段进行离散化。
ll y[maxn<<1];
int main(){
n=read();
n<<=1;
for(re int i=1;i<=n;i+=2){
xx=read();yy=read();x2=read();y2=read();
y[i]=yy,y[i+1]=y2;
}
sort(y+1,y+n+1);
int tot=unique(y+1,y+n+1)-y-1;
}
(@CYJian提供了一种不需要离散化的做法,可以用标记永久化和动态开点偷个懒)
离散化以后,会出现 \(tot\) 个不同的纵坐标值,于是我们的扫描线最多会被分成 \(tot-1\) 段。
我们开一个数组 \(cnt[]\) 来记录每一段被覆盖的次数。
扫描的过程中,如果当前四元组是 \((x_1,y_1,y_2,k)\) ,我们就把 \(cnt[y[y_1]],cnt[[y_1]+1],\cdots,cnt[[y_2]-1]\) 都加上 \(k\) 。
在扫到下一个四元组的过程中,被覆盖的长度就等于 \(\sum \limits_{c[i]>0} (y[i+1]-y[i])\)
对于 \(cnt\) 数组,我们可以使用线段树来维护,这样就可以 \(O(n^2)->O(nlogn)\)
线段树需要维护两个内容:
1.这个线段被覆盖了多少次
2.这个线段被整个矩形覆盖的长度
struct SegmentTree{
int l,r,sum;
ll len;
}st[maxn<<3];
对于一个四元组,我们在 \([y_1,y_2-1]\)
上执行区间修改操作。
对于线段树中任意一个节点 \([l,r]\) ,如果 \(sum>0\) 那么 \(len=y[r+1]-y[l]\),
否则, \(len\) 等于两个子节点的 \(len\) 之和。最后根节点的 \(len\) 就是整个扫描线上被覆盖的区间长度。
//#define LawrenceSivan
#include<bits/stdc++.h>
using namespace std;
const int maxn=1e6+5;
typedef long long ll;
#define re register
#define ls rt<<1
#define rs rt<<1|1
int n,cnt;
ll xx,yy,x2,y2,y[maxn<<1];
struct Line{
ll x,low,high;
int mark;
bool operator < (const Line &a)const{
return x < a.x;
}
}line[maxn<<1];
struct SegmentTree{
int l,r,sum;
ll len;
}st[maxn<<3];
void build(int rt,int l,int r){
st[rt].l=l,st[rt].r=r;
st[rt].len=0;
st[rt].sum=0;
if(l==r)return;
int mid=(l+r)>>1;
build(ls,l,mid);
build(rs,mid+1,r);
}
void push_up(int rt){
int l=st[rt].l,r=st[rt].r;
if(st[rt].sum)st[rt].len=y[r+1]-y[l];
else st[rt].len=st[ls].len+st[rs].len;
}
void modify(int rt,ll l,ll r,int c){
int ql=st[rt].l,qr=st[rt].r;
if(y[qr+1]<=l||r<=y[ql])return;
if(l<=y[ql]&&y[qr+1]<=r){
st[rt].sum+=c;
push_up(rt);
return;
}
modify(ls,l,r,c);
modify(rs,l,r,c);
push_up(rt);
}
inline ll read(){
ll x=0,f=1;char ch=getchar();
while(!isdigit(ch)){if(ch=='-')f=-1;ch=getchar();}
while(isdigit(ch)){x=x*10+(ch^48);ch=getchar();}
return x*f;
}
int main(){
#ifdef LawrenceSivan
freopen("horizon.in","r",stdin);
freopen("horizon.out","w",stdout);
#endif
n=read();
n<<=1;
for(re int i=1;i<=n;i+=2){
xx=read();yy=read();x2=read();y2=read();
y[i]=yy,y[i+1]=y2;
line[i]=(Line){xx,yy,y2,1};
line[i+1]=(Line){x2,yy,y2,-1};
}
sort(line+1,line+n+1);
sort(y+1,y+n+1);
int tot=unique(y+1,y+n+1)-y-1;
build(1,1,tot-1);
ll ans=0;
for(re int i=1;i<n;i++){
modify(1,line[i].low,line[i].high,line[i].mark);
ans+=st[1].len*(line[i+1].x-line[i].x);
}
printf("%lld",ans);
return 0;
}
T4
题目大概就是说对于一个长度为 \(n\) 的数,他会给出一些限制,每次限制形如 \([l_1,r_1]\),\([l_2,r_2]\),要求这个数的这两个区间对应位上的数字必须严格相等。
说白了就是一个填格子的问题;
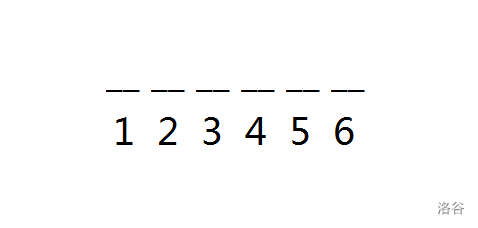
对样例的解释:
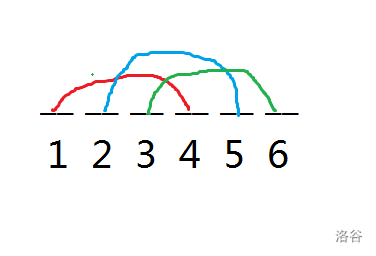
在 \([1,3]\), \([4,6]\) 这两个区间中,\(1,4;2,5;3,6\) 这几个数是严格一一对应的。于是我们可以把他们看成一对。
那么我们可以发现,对于长度为 \(n\) 的数,除了最高位以外,其他的每一位都可以填 \(0-9\) 以内的所有数,只有第一位不能填 \(0\) ,也就是其他的位有 \(10\) 种情况,最高位有 \(9\) 种情况。
在按照集合划分以后,我们的答案就是 \(9 \times 10^{cnt-1}\) (\(cnt\)是对数)
统计对数我们可以使用并查集,最后扫一遍 \(fa\) 数组,判断集合的个数。
复杂度 \(O(n^2logn)\)
考虑优化。
可以发现我们的统计是基于一个已知的值域,并且不需要在线处理,而且统计方式很固定,于是考虑倍增。
用 \(fa[i][k]\) 表示左端点是位置 \(i\) ,长度为 \(2^k\) 的区间 所在集合的根的左端点。
for(re int i=1,l1,r1,l2,r2;i<=m;i++){
l1=read();r1=read();l2=read();r2=read();
for(int k=maxk;k>=0;k--){
if(l1+(1<<k)-1<=r1){
merge(l1,l2,k),l1+=1<<k,l2+=1<<k;
}
}
}
最后统计答案的时候把所有层的对应端点合并即可
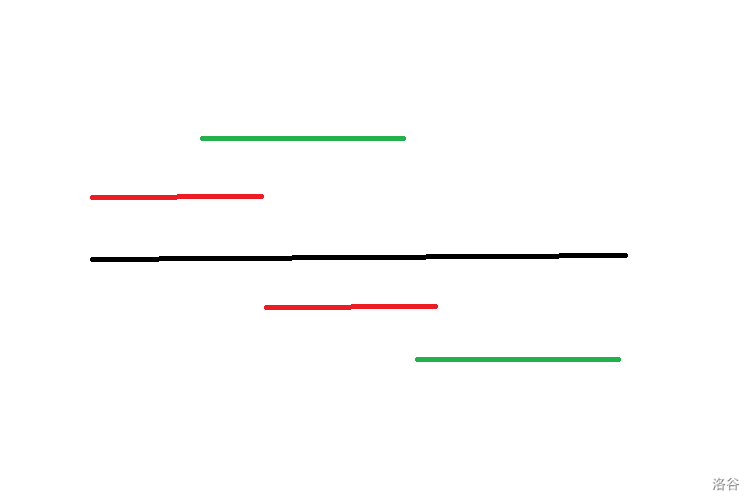
重复并不影响答案。
int pos=find(i,k);
merge(i,pos,k-1),merge(i+(1<<k-1),pos+(1<<k-1),k-1);
复杂度 \(O(nlog^2n)\)
最后扫一遍 \(fa\) 数组,数到底有多少对,然后计算答案。
for(re int i=1;i<=n;++i){
if(fa[i][0]==i){
if(ans==0)ans=9;
else (ans*=10)%=mod;
}
}
CODE:
//#define LawrenceSivan
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
#define re register
const int maxn=1e5+5;
const int mod=1e9+7;
#define INF 0x3f3f3f3f
int n,m;
ll ans;
int fa[maxn][21];
int maxk;
int find(int x,int k){
return x==fa[x][k]?x:fa[x][k]=find(fa[x][k],k);
}
void merge(int x,int y,int k){
x=find(x,k),y=find(y,k);
if(x!=y)fa[x][k]=y;
}
inline void init(){
for(int i=1;i<=n;i++){
for(int k=0;k<=maxk;k++){
fa[i][k]=i;
}
}
}
inline int read(){
int x=0,f=1;char ch=getchar();
while(!isdigit(ch)){if(ch=='-')f=-1;ch=getchar();}
while(isdigit(ch)){x=x*10+(ch^48);ch=getchar();}
return x*f;
}
int main(){
#ifdef LawrenceSivan
freopen("number.in","r",stdin);
freopen("number.out","w",stdout);
#endif
n=read();m=read();
maxk=log2(n);
init();
for(re int i=1,l1,r1,l2,r2;i<=m;i++){
l1=read();r1=read();l2=read();r2=read();
for(int k=maxk;k>=0;k--){
if(l1+(1<<k)-1<=r1){
merge(l1,l2,k),l1+=1<<k,l2+=1<<k;
}
}
}
for(re int k=maxk;k;k--){
for(re int i=1;i+(1<<k)-1<=n;i++){
int pos=find(i,k);
merge(i,pos,k-1),merge(i+(1<<k-1),pos+(1<<k-1),k-1);
}
}
for(re int i=1;i<=n;++i){
if(fa[i][0]==i){
if(ans==0)ans=9;
else (ans*=10)%=mod;
}
}
printf("%lld\n",ans);
return 0;
}

 2021.5.16模拟赛总结
2021.5.16模拟赛总结

 浙公网安备 33010602011771号
浙公网安备 33010602011771号