P3295 [SCOI2016]萌萌哒

P3295 [SCOI2016]萌萌哒

题目大概就是说对于一个长度为 \(n\) 的数，他会给出一些限制，每次限制形如 \([l_1,r_1]\),\([l_2,r_2]\),要求这个数的这两个区间对应位上的数字必须严格相等。

说白了就是一个填格子的问题；

对样例的解释：

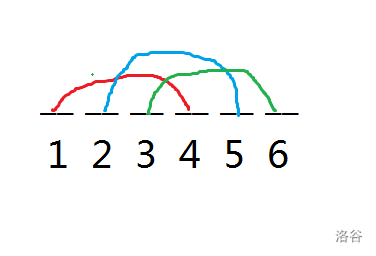
在 \([1,3]\)， \([4,6]\) 这两个区间中，\(1,4;2,5;3,6\) 这几个数是严格一一对应的。于是我们可以把他们看成一对。

那么我们可以发现，对于长度为 \(n\) 的数，除了最高位以外，其他的每一位都可以填 \(0-9\) 以内的所有数，只有第一位不能填 \(0\) ,也就是其他的位有 \(10\) 种情况，最高位有 \(9\) 种情况。

在按照集合划分以后，我们的答案就是 \(9 \times 10^{cnt-1}\) （\(cnt\)是对数）

统计对数我们可以使用并查集，最后扫一遍 \(fa\) 数组，判断集合的个数。

复杂度 \(O(n^2logn)\)

考虑优化。

可以发现我们的统计是基于一个已知的值域，并且不需要在线处理，而且统计方式很固定，于是考虑倍增。

用 \(fa[i][k]\) 表示左端点是位置 \(i\) ，长度为 \(2^k\) 的区间 所在集合的根的左端点。

for(re int i=1,l1,r1,l2,r2;i<=m;i++){
		l1=read();r1=read();l2=read();r2=read();
		for(int k=maxk;k>=0;k--){
			if(l1+(1<<k)-1<=r1){
				merge(l1,l2,k),l1+=1<<k,l2+=1<<k;
			}
		}
	}

最后统计答案的时候把所有层的对应端点合并即可

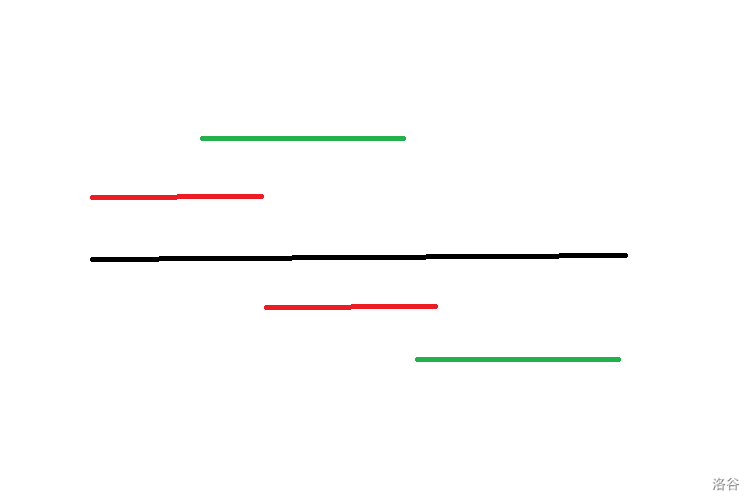
重复并不影响答案。

int pos=find(i,k);
merge(i,pos,k-1),merge(i+(1<<k-1),pos+(1<<k-1),k-1);

复杂度 \(O(nlog^2n)\)

最后扫一遍 \(fa\) 数组，数到底有多少对，然后计算答案。

for(re int i=1;i<=n;++i){
   	if(fa[i][0]==i){
   		if(ans==0)ans=9;
   		else (ans*=10)%=mod;
   	}
   }

CODE：

//#define LawrenceSivan

#include<bits/stdc++.h>
using namespace std;

typedef long long ll;
#define re register
const int maxn=1e5+5;
const int mod=1e9+7;
#define INF 0x3f3f3f3f

int n,m;
ll ans;
int fa[maxn][21];
int maxk;

int find(int x,int k){
   return x==fa[x][k]?x:fa[x][k]=find(fa[x][k],k);
}

void merge(int x,int y,int k){
   x=find(x,k),y=find(y,k);
   if(x!=y)fa[x][k]=y;
}

inline void init(){
   for(int i=1;i<=n;i++){
   	for(int k=0;k<=maxk;k++){
   		fa[i][k]=i;
   	}
   }
}

inline int read(){
   int x=0,f=1;char ch=getchar();
   while(!isdigit(ch)){if(ch=='-')f=-1;ch=getchar();}
   while(isdigit(ch)){x=x*10+(ch^48);ch=getchar();}
   return x*f;
}

int main(){
#ifdef LawrenceSivan
   freopen("number.in","r",stdin);
   freopen("number.out","w",stdout);
#endif
   n=read();m=read();
   maxk=log2(n);
   
   init();
   
   for(re int i=1,l1,r1,l2,r2;i<=m;i++){
   	l1=read();r1=read();l2=read();r2=read();
   	for(int k=maxk;k>=0;k--){
   		if(l1+(1<<k)-1<=r1){
   			merge(l1,l2,k),l1+=1<<k,l2+=1<<k;
   		}
   	}
   }
   
   for(re int k=maxk;k;k--){
   	for(re int i=1;i+(1<<k)-1<=n;i++){
   		int pos=find(i,k);
   		merge(i,pos,k-1),merge(i+(1<<k-1),pos+(1<<k-1),k-1);
   	}
   }
   	
   for(re int i=1;i<=n;++i){
   	if(fa[i][0]==i){
   		if(ans==0)ans=9;
   		else (ans*=10)%=mod;
   	}
   }
   	
   	
   printf("%lld\n",ans);


   return 0;
}