p3834 可持久化线段树模板（主席树）
可持久化线段树
主席树
前言
其实这个博客早就该发了，但是一直没有找到合适的时机。
今天补上。
简介
主席树，又称函数式线段树，是一种重要的可持久化数据结构。
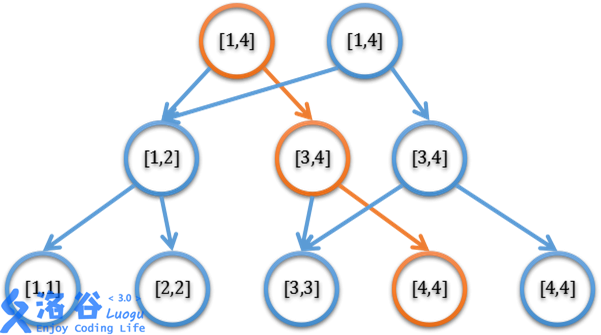
由于我们对于线段树的单点修改操作只会影响从根节点开始的 \(O(logn)\) 个节点，所以我们在维护历史版本的时候只需要对每个被更新的节点创捷一个副本。对于这个副本，如果他不是叶子节点，那么他的左右子树必定有一个是要更新的，于是我们递归地执行创建副本的操作，对于另外一个不改变的节点，我们直接把原来的线段树的对应部分粘贴过来就好了，相当于我们在原来的线段树上拉了一个新的链子。
实现
可以发现，这样操作以后我们的线段树就不再是一个完全二叉树，于是我们只能抛弃原来的二倍编码原则，而是采用一种新的方式记录节点：
#define ls(x) st[(x)].ls
#define rs(x) st[(x)].rs
struct segmenttree{
int ls,rs;
int v;
}st[maxn<<5];
int tot,root[maxn];
int n,a[maxn];
void build(int &t,int l,int r){
t=++tot;
if(l==r)return;
int mid=(l+r)>>1;
build(ls(t),l,mid);
build(rs(t),mid+1,r);
}
int main(){
build(root[0],1,R);
}
为了节省空间，我们不再记录每个节点代表的区间，而是作为参数传递。
对于第 \(i\) 次修改，我们直接以第 \(i-1\) 个版本为基础。
容易发现，可持久化线段树维护了历史版本。
可是还存在一些问题：可持久化线段树难以维护大部分区间修改操作，我们可以通过使用标记永久化来代替标记的下传。
但是有的时候区间修改是可以改变为单点修改，详细大家可以看 $NOIP\ 2012 $ 借教室。
例题
维护区间第 \(k\) 大是很经典的主席树题了，这个题有很多做法，比如值域分治，归并树和树套树，以及这里要说的主席树。
其他的自己了解吧。
首先思考一个问题：序列 \(A\) 中有多少个数字落在区间 \([L,R]\) 内 \(cnt[L,R]\),
我们只需要比较一下 \(cnt[L,mid]\) 和 \(k_i\) 的关系就可以确定 \(A\) 的第 \(k\) 小的数字是 \(\le mid\) 还是 $>mid $ ，从而选择进入线段树的左右子树之一。
对于本题，我们首先对于原序列进行离散化，之后我们在每个节点维护一个值 \(cnt\) ，就是这个值域区间有多少个数字插入过。
之后我们对于每个数，都在主席树上执行一次插入操作，同时维护 \(cnt\) 值。
int modify(int rt,int l,int r){
int t=++tot;
ls(t)=ls(rt),rs(t)=rs(rt);
st[t].v=st[rt].v+1;
if(l==r)return t;
int mid=(l+r)>>1;
if(x<=mid)ls(t)=modify(ls(t),l,mid);
else rs(t)=modify(rs(t),mid+1,r);
return t;
}
int main(){
for(re int i=1;i<=n;i++){
x=lower_bound(b+1,b+1+R,a[i])-b;
root[i]=modify(root[i-1],1,R);
}
}
之后就是查询的问题了。
考虑每个询问，首先我们明确，因为 \(root[l_i]\) 和 \(root[r_i]\) 为根的两颗线段树他们对于值域的划分显然是一样的。所以这就意味着，\(root[r_i]\) 的 值域区间 \([L,R]\) 的 \(cnt\) 减去 \(root[l_i-1]\) 的 值域区间 \([L,R]\) 的 \(cnt\) 就是 \(A[l_i,r_i]\) 中有多少数落在了 \([L,R]\) 中。
于是我们就可以计算出这个数字，并且用这个数字与我们需要找的排名进行比较，如果这个数字大于等于我们要查找的排名，就代表答案一定存在于左侧，于是进入左子树，否则进入右子树。
int query(int x,int y,int l,int r,int k){
int xx=st[ls(y)].v-st[ls(x)].v;
if(l==r)return l;
int mid=(l+r)>>1;
if(xx>=k)return query(ls(x),ls(y),l,mid,k);
else return query(rs(x),rs(y),mid+1,r,k-xx);
}
复杂度分析：
离散化进行一次排序，一次去重，复杂度 \(O(nlogn)\),
构建一颗主席树复杂度 \(O(nlogn)\),
插入 与统计 \(cnt\) \(O(nlogn)\)
查询 \(O(mlogn)\)
总复杂度 \(O((n+m)logn)\)
空间复杂度 \(O(nlogn)\)
代码
//#define LawrenceSivan
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
#define re register
const int maxn=2e5+5;
#define INF 0x3f3f3f3f
#define ls(x) st[(x)].ls
#define rs(x) st[(x)].rs
int tot,n,m;
int ans,R,x;
struct node{
int ls,rs;
int v;
}st[maxn<<5];
int root[maxn],a[maxn],b[maxn];
void build(int &t,int l,int r){
t=++tot;
if(l==r)return;
int mid=(l+r)>>1;
build(ls(t),l,mid);
build(rs(t),mid+1,r);
}
int modify(int rt,int l,int r){
int t=++tot;
ls(t)=ls(rt),rs(t)=rs(rt);
st[t].v=st[rt].v+1;
if(l==r)return t;
int mid=(l+r)>>1;
if(x<=mid)ls(t)=modify(ls(t),l,mid);
else rs(t)=modify(rs(t),mid+1,r);
return t;
}
int query(int x,int y,int l,int r,int k){
int xx=st[ls(y)].v-st[ls(x)].v;
if(l==r)return l;
int mid=(l+r)>>1;
if(xx>=k)return query(ls(x),ls(y),l,mid,k);
else return query(rs(x),rs(y),mid+1,r,k-xx);
}
inline int read(){
int x=0,f=1;char ch=getchar();
while(!isdigit(ch)){if(ch=='-')f=-1;ch=getchar();}
while(isdigit(ch)){x=x*10+(ch^48);ch=getchar();}
return x*f;
}
int main(){
#ifdef LawrenceSivan
freopen("aa.in","r",stdin);
freopen("aa.out","w",stdout);
#endif
n=read();m=read();
for(re int i=1;i<=n;i++){
a[i]=read();
b[i]=a[i];
}
sort(b+1,b+1+n);
R=unique(b+1,b+1+n)-b-1;
build(root[0],1,R);
for(re int i=1;i<=n;i++){
x=lower_bound(b+1,b+1+R,a[i])-b;
root[i]=modify(root[i-1],1,R);
}
while(m--){
int l=read(),r=read(),k=read();
ans=query(root[l-1],root[r],1,R,k);
printf("%d\n",b[ans]);
}
return 0;
}
