莫队全家桶
今天学习了莫队
实在是太有魅力了
来写个学习笔记
莫队
普通莫队
莫队讲解
一,什么是莫队
莫队其实就是一种优雅的暴力,它十分玄学巧妙地将分块和暴力结合在了一起,主要用来处理离线区间查询等问题
由于莫队算法是由莫涛队长提出的,因此我们称这种算法为莫队
二,莫队原理
大概说一下,莫队就是对询问进行排序,然后通过左右端点的移动来维护区间信息。
那显而易见,莫队是离线算法
当然莫队还有一些神奇的拓展:带修莫队,回滚莫队等等(等我学会了再来补博客
三,莫队的操作过程
1,对于多段区间的询问,先将询问离线存储下来,然后再从左到右扫一遍,在过程中维护一段区间,就可以得到每个询问的答案.
2,但暴力扫肯定不行,所以在扫的过程中,需要对 \(l\) 进行排序,以求能够在移动次数最少的情况下,得到所有希望求出的区间.(就是说,我们要调整\(m\)次询问的顺序,使之有序,这样我们在移动时,就可以不反复来回移动,而单向的用较少的次数就可以进行维护与查询操作
3,首先对每个区间进行分块操作,再将左端点在一起的区间询问放在一起进行处理,对于每个块处理一遍,那么就可以得到所有询问的答案.(分块的结合就是在这里
最严格的顺序是每个区间求一次曼哈顿距离最小生成树
四,莫队的代码实现
自然我们要记录原数组,还要开一个 \(cnt\) (用于统计答案个数,还有一个答案数组
ll ans[maxn],sum;
int a[maxn],cnt[maxn],lal=1,lar=0;//lal lar分别是上一次的左右端点
按照顺序如何处理呢?
把 \([1,n]\) 分成$ \sqrt n$ 块
还有一种奇妙而玄学的分法:
block=n/sqrt(m*2/3);
这样会更快一些;
我们先把这些区间按照左端点 \(l\) 所在的块从左往右排序
再把l所在块相同的区间按 \(r\) 从小到大排序
结构体数组存储查询的区间以及下标
struct node{
int l,r,id;//l是左端点,r是右端点,id是下标
inline bool operator < (const node &a)const{
return (belong[l]==belong[a.l])?r<a.r:belong[l]<belong[a.l];
}
}mocap[maxn];//mo captain,即莫队
这里再提一种玄学的玩意,名曰:奇偶优化
按奇偶块排序。这也是比较通用的。如果区间左端点所在块不同,那么就直接按左端点从小到大排;如果相同,奇块按右端点从小到大排,偶块按右端点从大到小排。
inline bool operator < (const node &a)const{
return belong[l]^belong[a.l]?belong[l]<belong[a.l]:((belong[l]&1)?r<a.r:r>a.r);
}
排好了序自然就要开始进行询问和维护操作了
这里也正是莫队的精髓
for(re int i=1;i<=m;i++){
int l=mocap[i].l,r=mocap[i].r;
while(lal>l)lal--,add(a[lal]);
while(lar<r)lar++,add(a[lar]);
while(lal<l)del(a[lal]),lal++;
while(lar>r)del(a[lar]),lar--;
ans[mocap[i].id]=sum;
}
想象一个区间的移动;
\(add\) 和 \(del\) 函数
inline void add(int x){
sum+=2*cnt[x]+1;
cnt[x]++;
}
inline void del(int x){
sum-=2*cnt[x]-1;
cnt[x]--;
}
五,莫队的复杂度证明
对于区间进行分块那么可以得到 \(\sqrt{n}\) 个块,那么对于就存在于 \(\sqrt{n}\) 个区间,而每次对于每个区间块中的 \(l,r\) 的最坏情况是对于每个块都遍历到序列的最右端,共 \(n\) 个点.每次移动指针复杂度为 \(O(1)\) ,所以整个算法的复杂度 \(O (n\sqrt{n})\)
(真是太美妙了
例题:
洛谷 P2709 小B的询问
CODE:
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
#define re register
const int maxn=5e5+5;
int n,m,k,block;
ll ans[maxn],sum;
int a[maxn],cnt[maxn],lal=1,lar=0;
struct node{
int l,r,id;
inline bool operator < (const node &a)const{
return ((l-1)/block==(a.l-1)/block)?r<a.r:l/block<a.l/block;
}
}mocap[maxn];
inline int read(){
int x=0,f=1;char ch=getchar();
while(!isdigit(ch)){if(ch=='-')f=-1;ch=getchar();}
while(isdigit(ch)){x=x*10+(ch^48);ch=getchar();}
return x*f;
}
inline void add(int x){
sum+=2*cnt[x]+1;
cnt[x]++;
}
inline void del(int x){
sum-=2*cnt[x]-1;
cnt[x]--;
}
int main(){
n=read();m=read();k=read();
block=sqrt(n);
for(re int i=1;i<=n;i++){
a[i]=read();
}
for(re int i=1;i<=m;i++){
mocap[i].l=read();
mocap[i].r=read();
mocap[i].id=i;
}
sort(mocap+1,mocap+1+m);
for(re int i=1;i<=m;i++){
int l=mocap[i].l,r=mocap[i].r;
while(lal>l)lal--,add(a[lal]);
while(lar<r)lar++,add(a[lar]);
while(lal<l)del(a[lal]),lal++;
while(lar>r)del(a[lar]),lar--;
ans[mocap[i].id]=sum;
}
for(re int i=1;i<=m;i++){
printf("%lld\n",ans[i]);
}
return 0;
}
洛谷 P1494 [国家集训队]小Z的袜子
首先我们明确莫队一般来讲是只能搞一个区间内某一些东西的出现次数的,如果让我们去求出概率该怎么办呢?
我们用 \(cnt\) 数组来记录区间 \([l,r]\) 内某种颜色的袜子出现的次数.
我们考虑在区间 \([l,r]\) 中取出两个相同颜色 \(x\) 的情况有:
\(C_{cnt[x]}^2= \dfrac{cnt[x] \times (cnt[x]-1)}{2}\)
在区间 \([l,r]\) 中取出两个任意颜色的情况有:
\(C_{len}^2= \dfrac{len \times (len-1)}{2}\)
于是在区间 \([l,r]\) 中取出两个相同颜色 \(x\) 的概率就可以搞得出来了:
\(C_{cnt[x]}^2= \dfrac{cnt[x] \times (cnt[x]-1)}{len \times (len-1)}=\dfrac{cnt[x] \times (cnt[x]-1)}{(r-l+1) \times (r-l)}=\dfrac{cnt[x]^2-cnt[x]}{(r-l+1) \times (r-l)}\)
于是在区间内抽到两个相同数字的概率就是:
\(\sum\limits_{i=1}^n \dfrac{cnt[i]^2-cnt[i]}{(r-l+1) \times (r-l)}= \dfrac{\sum\limits_{i=1}^n cnt[i]^2-cnt[i]}{(r-l+1) \times (r-l)}\)
对于区间 \([l,r]\) 我们有
\(\sum\limits_{i=1}^n cnt[i]=r-l+1\)
所以答案为:
\(\dfrac{\sum\limits_{i=1}^n cnt[i]^2-(r-l+1)}{(r-l+1) \times (r-l)}\)
最后只需要用 \(gcd\) 化简就可以了.
于是我们用 \(cnt\) 数组维护平方和.
CODE:
//#define LawrenceSivan
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
#define re register
const int maxn=5e5+5;
#define INF 0x3f3f3f3f
int n,m,k,a[maxn],ans[maxn],lal=1,lar=0,sum,block,cnt[maxn];
ll l1[maxn],r1[maxn];
struct node{
int l,r,id;
inline bool operator < (const node &a)const{
return ((l-1)/block==(a.l-1)/block)?r<a.r:l/block<a.l/block;
}
}mocap[maxn];
ll gcd(int a,int b){
return b==0?a:gcd(b,a%b);
}
inline void add(int x){
sum-=cnt[x]*(cnt[x]-1)/2;
cnt[x]++;
sum+=cnt[x]*(cnt[x]-1)/2;
}
inline void del(int x){
sum-=cnt[x]*(cnt[x]-1)/2;
cnt[x]--;
sum+=cnt[x]*(cnt[x]-1)/2;
}
inline int read(){
int x=0,f=1;char ch=getchar();
while(!isdigit(ch)){if(ch=='-')f=-1;ch=getchar();}
while(isdigit(ch)){x=x*10+(ch^48);ch=getchar();}
return x*f;
}
int main(){
#ifdef LawrenceSivan
freopen("aa.in","r",stdin);
freopen("aa.out","w",stdout);
#endif
n=read();m=read();
block=n/sqrt(m*2/3);
for(re int i=1;i<=n;i++){
a[i]=read();
}
for(re int i=1;i<=m;i++){
mocap[i].l=read();mocap[i].r=read();mocap[i].id=i;
l1[i]=mocap[i].l,r1[i]=mocap[i].r;
}
sort(mocap+1,mocap+1+m);
for(re int i=1;i<=m;i++){
int l=mocap[i].l,r=mocap[i].r;
while(lal>l)lal--,add(a[lal]);
while(lar<r)lar++,add(a[lar]);
while(lal<l)del(a[lal]),lal++;
while(lar>r)del(a[lar]),lar--;
ans[mocap[i].id]=sum;
}
for(re int i=1;i<=m;i++){
int tmp;
tmp=gcd((ll)ans[i],(ll)(r1[i]-l1[i]+1)*(r1[i]-l1[i])/2);
if(l1[i]==r1[i])printf("0/1\n");
else printf("%d/%lld\n",ans[i]/tmp,(ll)((r1[i]-l1[i]+1)*(r1[i]-l1[i])/2)/tmp);
}
return 0;
}
带修莫队
其实这道题在智能推荐里躺了很久了,但是我一直没有打开他,然后还一直大喊lj洛谷为什么没有带修莫队的板子题
wssb
首先我们知道普通的莫队是不能修改的。
因为我们每个询问的答案都是根据上一次询问的答案稍加调整得出来的,于是每一次修改操作就会导致对答案产生了严重的影响。
于是我们想办法消除这种影响。
考虑把查询操作和修改操作分别记录下来。
在记录查询操作的时候,需要增加一个变量来记录离本次查询最近的修改的位置(这种玩意其实类似于 \(HH\) 的项链)
然后需要用一个变量记录当前已经进行了几次修改.
对于查询操作,如果上一次改的比本次查询需要改的少,就改过去
反之如果改多了就改回来。
简单来说,就是比较这次与上一次修改的操作次数不一样,我们就暴力的搞成一样的就行了。
也有一种说法是,在原有的 \(l\) , \(r\) 的基础上,增加一个时间轴 \(t\) ,如果 \(t\) 在 \(l\) , \(r\) 之间就更新。
关于结构体的改进:
struct MOCAP{//其实结构体应该开两个,就是说查询和修改都开,但是为了简便,我直接开了一个,一表两用
int l,r,id,pre;//l和r分别是查询中的左右端点和更改中的位置以及权值
inline bool operator < (const MOCAP &a)const{//改进后的排序
return belong[l]==belong[a.l]?(belong[r]==belong[a.r]?pre<a.pre:belong[r]<belong[a.r]):belong[l]<belong[a.l];
}
}mocap[maxn],modi[maxn];
排序的方法:
- 关于左右端点的排序,与原来是一样的。
- 关于修改的排序,修改位置在前面的就排在前面
之后还有一个问题,就是说虽然是存在修改操作的,但是之后再查询的区间内进行修改对答案才是有影响的。
所以在暴力调整修改的时候保证一下区间端点位置就行了
之后还有一个小细节:在每次修改操作之后,下一次的操作一定是与这步是相反的
也就是改后->还原->修改->还原
所以我们直接交换就行了:
inline void update(int x,int t){
if(mocap[x].l<=modi[t].l&&mocap[x].r>=modi[t].l){
del(a[modi[t].l]);
add(modi[t].r);
}
swap(a[modi[t].l],modi[t].r);
}
于是最后的操作就是这样的:
for(re int i=1;i<=cntq;i++){
while(l>mocap[i].l)l--,add(a[l]);
while(l<mocap[i].l)del(a[l]),l++;
while(r>mocap[i].r)del(a[r]),r--;
while(r<mocap[i].r)r++,add(a[r]);
while(t<mocap[i].pre)t++,update(i,t);//改少了
while(t>mocap[i].pre)update(i,t),t--;//改多了
ans[mocap[i].id]=sum;
}
最后优化块长:
- 时间上的优化:将块的大小从 \(sqrt(n)\) 改为 $n $的二分之三次方:
block=pow(n,(double)2/(double)3);
然后复杂度大概就是 \(O( n^ \frac {5}{3})\).
CODE:
//#define LawrenceSivan
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
#define INF 0x3f3f3f3f
#define re register
const int maxn=3e5+5;
const int maxm=2e6+5;
int n,m,block;
int l=1,r,t;
int sum,c[maxm],a[maxn],ans[maxn],belong[maxn];
char op[5];
struct MOCAP{
int l,r,id,pre;
inline bool operator < (const MOCAP &a)const{
return belong[l]==belong[a.l]?(belong[r]==belong[a.r]?pre<a.pre:belong[r]<belong[a.r]):belong[l]<belong[a.l];
}
}mocap[maxn],modi[maxn];
int cntq,cntc;
inline void add(int x){
sum+= (++c[x]==1);
}
inline void del(int x){
sum-= (--c[x]==0);
}
inline void update(int x,int t){
if(mocap[x].l<=modi[t].l&&mocap[x].r>=modi[t].l){
del(a[modi[t].l]);
add(modi[t].r);
}
swap(a[modi[t].l],modi[t].r);
}
inline int read(){
int x=0, f=1;char ch=getchar();
while (!isdigit(ch)) {if(ch=='-')f=-1;ch=getchar();}
while (isdigit(ch)){x=x*10+(ch^48);ch=getchar();}
return x*f;
}
int main() {
#ifdef LawrenceSivan
freopen("aa.in", "r", stdin);
freopen("aa.out", "w", stdout);
#endif
n=read();m=read();
block=pow(n,(double)2/(double)3);
for(re int i=1;i<=n;i++){
a[i]=read();
belong[i]=(i-1)/block+1;
}
for(re int i=1;i<=m;i++){
cin>>op;
if(op[0]=='Q'){
mocap[++cntq].l=read();
mocap[cntq].r=read();
mocap[cntq].pre=cntc;
mocap[cntq].id=cntq;
}
if(op[0]=='R'){
modi[++cntc].l=read();//注意这里的l指的是修改位置pos
modi[cntc].r=read();//注意这里的r是修改权值val
}
}
sort(mocap+1,mocap+1+cntq);
for(re int i=1;i<=cntq;i++){
while(l>mocap[i].l)l--,add(a[l]);
while(l<mocap[i].l)del(a[l]),l++;
while(r>mocap[i].r)del(a[r]),r--;
while(r<mocap[i].r)r++,add(a[r]);
while(t<mocap[i].pre)t++,update(i,t);
while(t>mocap[i].pre)update(i,t),t--;
ans[mocap[i].id]=sum;
}
for(re int i=1;i<=cntq;i++){
printf("%d\n",ans[i]);
}
return 0;
}
树上莫队
SP10707 COT2 - Count on a tree II
这就是树上莫队板子题了。
顾名思义,树上莫队就是树上的莫队这不nm废话吗
所以显然我们的策略就是要首先对树进行树剖,然后转化成线性结构,然后我们大力搞莫队就行了。
那么问题就来了,如何把他变成线性结构?
前置知识 欧拉序
众所周知,我们对树的遍历通常是两种序。如果不知道那你现在知道了
分别是 \(DFS\) 序和欧拉序。首先来区别一下这两种序。
DFS序
如图,我们的 \(dfs\) 一般是这样的
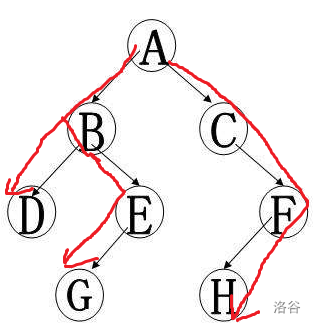
这张图的dfs序为A-B-D-E-G-C-F-H
好 \(DFS\) 就说完了。
什么??这就说完了?
确实,毕竟咱这里主要不说这玩意
接下来进入正题,欧拉序!
欧拉序
欧拉序就是从根结点出发,按dfs的顺序在绕回原点所经过所有点的顺序
所以对于这棵树,他的欧拉序就是这样的:
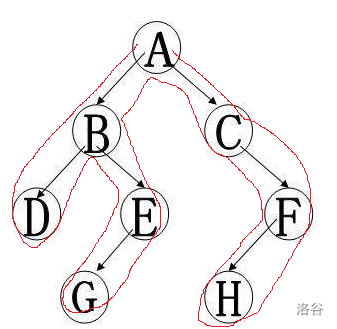
欧拉序为A-B-D-D-E-G-G-E-B-C-F-H-H-F-C-A
其实欧拉序是有两种的,一种是记录入度个,另一个是入度和出度都记录。
树上莫队用的是第二种,也就是我们上面说到的这种。
本题
为什么要用到欧拉序呢?
首先回顾一下题意,要求我们找到一条路径上的颜色个数,也就是不同的数字个数。
从欧拉序的形式上看,我们其实可以借助欧拉序去找一找路径上究竟有哪些点,以及该如何记录。
这里我们设 \(st[i]\) 表示访问到 \(i\) 时加入欧拉序的时间,\(ed[i]\) 表示回溯经过 \(i\) 时加入欧拉序的时间
不妨设 \(st[x]\)<\(st[y]\)(也就是先访问 \(x\),再访问 \(y\))
分情况讨论;
情况一:
如果 \(LCA(x,y)=x\) ,这显然说明 \(x\),\(y\) 在同一条路径上。
于是我们取出 \(st[x]\) 到 \(st[y]\) 这一段区间,有的点会出现两次,有的点出现一次,应该明确出现两次的点对答案是没有贡献的,因为它进入了递归又在回溯时出去了,这证明这条路径一定是不经过这个子树的,于是我们只需要统计路径上出现两次的点。
我们拿上面的图来举例子:

如果两个点分别是 \(A\),\(G\) ,那么 \(st[A]-st[G]\) 显然是 \(A-B-D-D-E-G\)
出现两次的点是 \(D\)。
于是我们发现我们的路径 \(A-G\) 上恰好是没有点 \(D\) 的,于是……
懂了吧
情况二:
如果 \(LCA(x,y) \ne x\) ,这显然说明 \(x\),\(y\) 在两棵不同的子树内。
于是我们取出 \(ed[x]-st[y]\)

依然对于这张图,我们举例子:
如果两个点分别是 \(D\),\(C\)
于是 \(ed[D]-st[C]\) 显然就是:
\(D-E-G-G-E-B-C\)
同样的,我们只统计出现一次的点,两次的点也不统计。
但是有这样一个问题,我们上面的过程是有一个小问题的。
我们没有统计 \(LCA\) !
后果不太严重,加上就好了 /cy
至于如何判断第一次与第二次的问题,这个很简单,我们多记录一个 \(use[x]\),表示 \(x\) 这个点有没有被加入,每次处理的时候如果 \(use[x]=0\) 则需要添加节点;如果 \(use[x]=1\) 则需要删除节点,每次处理之后都对 \(use[x]\) 异或 \(1\) 就可以了.
inline void calc(int x){
used[x]?del(x):add(x);
used[x]^=1;
}
下面是一些细节
- 欧拉序直接用树剖就行了,在 \(dfs1\) 中顺便就搞出来了。
\(LCA\) 顺便也就搞出来了,多香
void dfs1(int u,int f){
fa[u]=f;
size[u]=1;
deep[u]=deep[f]+1;
st[u]=++tot;
pot[tot]=u;
for(re int i=head[u];i;i=nxt[i]){
int v=to[i];
if(v==f)continue;
dfs1(v,u);
size[u]+=size[v];
if(size[v]>size[son[u]])son[u]=v;
}
ed[u]=++tot;pot[tot]=u;
}
void dfs2(int u,int topf){
top[u]=topf;
if(!son[u])return;
dfs2(son[u],topf);
for(re int i=head[u];i;i=nxt[i]){
int v=to[i];
if(top[v])continue;
dfs2(v,v);
}
}
inline int LCA(int x,int y){
while(top[x]!=top[y]){
if(deep[top[x]]<deep[top[y]])swap(x,y);
x=fa[top[x]];
}
return deep[x]<deep[y]?x:y;
}
- 一定要记得,欧拉序的长度是节点长度的 \(2\) 倍,所以分块的时候要分 \(n<<1\)
for(re int i=1;i<=(n<<1);i++){
belong[i]=i/block+1;
}
- 这个题要离散化。
inline void Discretization(){
sort(data+1,data+1+n);
int len=unique(data+1,data+1+n)-data-1;
for(re int i=1;i<=n;i++) a[i]=lower_bound(data+1,data+1+len,a[i])-data;
}
其实我觉得还是挺恶心的
CODE:
//#define LawrenceSivan
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
#define re register
const int maxn=1e5+5;
#define INF 0x3f3f3f3f
int n,m,block;
int a[maxn],data[maxn];
int st[maxn],ed[maxn],tot;
int belong[maxn];
struct MOCAP{
int l,r,id,lca,ans;
inline bool operator < (const MOCAP &a)const{
return belong[l]==belong[a.l]?r<a.r:belong[l]<belong[a.l];
}
}mocap[maxn];
int nxt[maxn<<1],to[maxn<<1],head[maxn],cnt;
inline void add(int u,int v){
nxt[++cnt]=head[u];
to[cnt]=v;
head[u]=cnt;
}
int deep[maxn],fa[maxn],top[maxn],son[maxn],size[maxn],pot[maxn];
void dfs1(int u,int f){
fa[u]=f;
size[u]=1;
deep[u]=deep[f]+1;
st[u]=++tot;
pot[tot]=u;
for(re int i=head[u];i;i=nxt[i]){
int v=to[i];
if(v==f)continue;
dfs1(v,u);
size[u]+=size[v];
if(size[v]>size[son[u]])son[u]=v;
}
ed[u]=++tot;pot[tot]=u;
}
void dfs2(int u,int topf){
top[u]=topf;
if(!son[u])return;
dfs2(son[u],topf);
for(re int i=head[u];i;i=nxt[i]){
int v=to[i];
if(top[v])continue;
dfs2(v,v);
}
}
inline void Discretization(){
sort(data+1,data+1+n);
int len=unique(data+1,data+1+n)-data-1;
for(re int i=1;i<=n;i++) a[i]=lower_bound(data+1,data+1+len,a[i])-data;
}
inline int LCA(int x,int y){
while(top[x]!=top[y]){
if(deep[top[x]]<deep[top[y]])swap(x,y);
x=fa[top[x]];
}
return deep[x]<deep[y]?x:y;
}
int used[maxn],c[maxn],sum,ans[maxn];
int l=1,r=0;
inline void add(int x){
sum+=(++c[a[x]]==1);
}
inline void del(int x){
sum-=(--c[a[x]]==0);
}
inline void calc(int x){
used[x]?del(x):add(x);
used[x]^=1;
}
inline int read(){
int x=0,f=1;char ch=getchar();
while(!isdigit(ch)){if(ch=='-')f=-1;ch=getchar();}
while(isdigit(ch)){x=x*10+(ch^48);ch=getchar();}
return x*f;
}
int main(){
#ifdef LawrenceSivan
freopen("aa.in","r",stdin);
freopen("aa.out","w",stdout);
#endif
n=read();m=read();
block=n/sqrt(m*2/3);
for(re int i=1;i<=n;i++){
a[i]=data[i]=read();
}
for(re int i=1;i<=(n<<1);i++){
belong[i]=i/block+1;
}
Discretization();
for(re int i=1,x,y;i<n;i++){
x=read();y=read();
add(x,y);
add(y,x);
}
deep[1]=1;
dfs1(1,0);
dfs2(1,1);
for(re int i=1,x,y;i<=m;i++){
x=read();y=read();
if(st[x]>st[y])swap(x,y);
int lca=LCA(x,y);
mocap[i].id=i;
if(lca==x) mocap[i].l=st[x],mocap[i].r=st[y];
else mocap[i].l=ed[x],mocap[i].r=st[y],mocap[i].lca=lca;
}
sort(mocap+1,mocap+1+m);
for(re int i=1;i<=m;i++){
while(l<mocap[i].l)calc(pot[l]),l++;
while(l>mocap[i].l)l--,calc(pot[l]);
while(r<mocap[i].r)r++,calc(pot[r]);
while(r>mocap[i].r)calc(pot[r]),r--;
if(mocap[i].lca)calc(mocap[i].lca);
mocap[i].ans=sum;
if(mocap[i].lca)calc(mocap[i].lca);
}
for(re int i=1;i<=m;i++){
ans[mocap[i].id]=mocap[i].ans;
}
for(re int i=1;i<=m;i++){
printf("%d\n",ans[i]);
}
return 0;
}
练习题:P4074 [WC2013] 糖果公园
好啦,你现在学到了带修莫队和树上莫队的精髓啦,快来做这道超级无敌傻逼二合一题目吧!
想当年我第一次见他的时候他还是个黑的,几天不见这么拉了
首先可以注意到这玩意的题目真的是非常长,这就预示着这是一道非常非常非常毒瘤的题目。
其实也没有很毒瘤,只是因为我太菜调不出来而已
简要题意:
-
给定一张 \(n\) 个节点的树形图,每个节点 \(i\) 有一种颜色 \(C_i\),权值是 \(V_{C_i}\)(各个节点可能会有同样的颜色)。
-
每次讯问
(?一条路径,对于其中的每一个节点,经过时可以获得 \(V_i\times W_i\) 的贡献. -
每次经过同样的颜色时,\(W_i\) 会发生变化。
-
求路径上 \(\sum \limits_{C} val_c \sum \limits_{i=1}^{cnt_c}W_i\)
于是这就是比较显然的莫队了。
只不过他不仅要查询,而且还要支持更改操作。
于是这要求我们的莫队还得要带修。
于是就可以发现这是一道树上莫队加带修莫队的题了。
还是一样的思路,首先解决莫队上树的问题。
参考上面的树上莫队,首先需要使用欧拉序将树上路径提取出来使之成为线性结构,之后再进行莫队操作
依然使用树剖,顺带过程中求出 LCA
namespace Tree_chain_partition{
int fa[maxn],size[maxn],son[maxn],dep[maxn],top[maxn];
int st[maxn],ed[maxn],pot[maxn],dfn;
//前括号序st,后括号序ed,存储欧拉序的pot,以及时间戳
void dfs1(int u,int f){//树剖同时记录欧拉序
st[u]=++dfn;pot[dfn]=u;
size[u]=1;
fa[u]=f;
dep[u]=dep[f]+1;
for(re int i=head[u];i;i=nxt[i]){
int v=to[i];
if(v==f)continue;
dfs1(v,u);
size[u]+=size[v];
if(size[v]>size[son[u]])son[u]=v;
}
ed[u]=++dfn;pot[dfn]=u;
}
void dfs2(int u,int topf){
top[u]=topf;
if(!son[u])return;
dfs2(son[u],topf);
for(re int i=head[u];i;i=nxt[i]){
int v=to[i];
if(v==fa[u]||v==son[u])continue;
dfs2(v,v);
}
}
inline int lca(int x,int y){
while(top[x]!=top[y]){
if(dep[top[x]]<dep[top[y]])swap(x,y);
x=fa[top[x]];
}
return dep[x]<dep[y]?x:y;
}
}
之后考虑带修的问题。
回忆上面讲过的带修莫队,需要在莫队基础上增加一个维度。
排序依旧是先按照左端点,其次是右端点,最后是时间维度。
int belong[maxn];
struct Mocap{
int l,r,id,lca,ans,pre;
int pos,val;
inline bool operator < (Mocap &a)const{
return belong[l]==belong[a.l]?
belong[r]==belong[a.r]?
pre<a.pre:
belong[r]<belong[a.r]:
belong[l]<belong[a.l];
}
}mocap[maxn],modi[maxn];
修改操作和查询操作的记录完全可以使用同一个结构体,比较方便,缺点是一个结构体里面变量太多,可能不大好调试
读入操作的时候和普通的树上莫队与带修莫队差别并不算大,直接把他们融合一下。
别忘了记录时间维度
for(re int i=1,op;i<=q;i++){
read(op);
if(op==0){
read(modi[++cntm].pos);
read(modi[cntm].val);
}
if(op==1){
int x,y;
read(x),read(y);
if(st[x]>st[y])swap(x,y);
int LCA=lca(x,y);
mocap[++cntq].id=cntq,mocap[cntq].pre=cntm;//记录时间维度
if(LCA==x)mocap[cntq].l=st[x],mocap[cntq].r=st[y];
else mocap[cntq].l=ed[x],mocap[cntq].r=st[y],mocap[cntq].lca=LCA;
}
}
对于过程中的移动操作,依然需要借用欧拉序节点重复的原理,使用访问判断,而不能使用一般莫队的直接 add 与 del 操作。
ll c[maxn],sum;
inline void add(int x){
sum+= V[C[x]]*W[++c[C[x]]];
}
inline void del(int x){
sum-= V[C[x]]*W[c[C[x]]--];
}
bool vis[maxn];
inline void calc(int x){
vis[x]?del(x):add(x);
vis[x]^=1;
}
移动完了区间别忘了还要把修改也暴力调整一下。
inline void update(int x){
if(vis[modi[x].pos]){
calc(modi[x].pos);
swap(C[modi[x].pos],modi[x].val);
calc(modi[x].pos);
}
else swap(C[modi[x].pos],modi[x].val);
}
lca 的贡献不要忘记。
for(re int i=1;i<=cntq;i++){
while(l>mocap[i].l)calc(pot[--l]);//常规莫队
while(l<mocap[i].l)calc(pot[l++]);
while(r>mocap[i].r)calc(pot[r--]);
while(r<mocap[i].r)calc(pot[++r]);
while(tim<mocap[i].pre)update(++tim);//修改
while(tim>mocap[i].pre)update(tim--);
if(mocap[i].lca)calc(mocap[i].lca);//统计lca贡献
ans[mocap[i].id]=sum;
if(mocap[i].lca)calc(mocap[i].lca);
}
大概到这里就算是结束了,虽然过程非常繁琐,码量也不算小,但是如果封装几个 namespace 其实还是会好调很多的。
强烈谴责搞这么多读入,还有这么长的题面
注意事项
- 由于使用了欧拉序来提出序列,所以一条路径会变成原来的两倍,在分块的时候千万不要忘记这个事情。
- 同理由于上面的原因,数组也需要开两倍空间(这就是我 WA 了这么长时间的原因
- 一定要记得开
long long!
就这么多。
留个代码吧
//#define LawrenceSivan
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
#define INF 0x3f3f3f3f
#define re register
const int maxn=2e5+5;
#define int ll
#define debug cerr<<"!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!"<<endl;
int n,m,q,block;
int head[maxn],to[maxn<<1],nxt[maxn<<1],cnt;
inline void add(int u,int v){
nxt[++cnt]=head[u];
to[cnt]=v;
head[u]=cnt;
}
int V[maxn],W[maxn],C[maxn];
namespace MOCAP{
int belong[maxn];
struct Mocap{
int l,r,id,lca,ans,pre;
int pos,val;
inline bool operator < (Mocap &a)const{
return belong[l]==belong[a.l]?
belong[r]==belong[a.r]?
pre<a.pre:
belong[r]<belong[a.r]:
belong[l]<belong[a.l];
}
}mocap[maxn],modi[maxn];
int cntm,cntq,l=1,r,tim=0;
ll c[maxn],sum;
inline void add(int x){
sum+= V[C[x]]*W[++c[C[x]]];
}
inline void del(int x){
sum-= V[C[x]]*W[c[C[x]]--];
}
bool vis[maxn];
inline void calc(int x){
vis[x]?del(x):add(x);
vis[x]^=1;
}
inline void update(int x){
if(vis[modi[x].pos]){
calc(modi[x].pos);
swap(C[modi[x].pos],modi[x].val);
calc(modi[x].pos);
}
else swap(C[modi[x].pos],modi[x].val);
}
ll ans[maxn];
}
using namespace MOCAP;
namespace Tree_chain_partition{
int fa[maxn],size[maxn],son[maxn],dep[maxn],top[maxn];
int st[maxn],ed[maxn],pot[maxn],dfn;
void dfs1(int u,int f){
st[u]=++dfn;pot[dfn]=u;
size[u]=1;
fa[u]=f;
dep[u]=dep[f]+1;
for(re int i=head[u];i;i=nxt[i]){
int v=to[i];
if(v==f)continue;
dfs1(v,u);
size[u]+=size[v];
if(size[v]>size[son[u]])son[u]=v;
}
ed[u]=++dfn;pot[dfn]=u;
}
void dfs2(int u,int topf){
top[u]=topf;
if(!son[u])return;
dfs2(son[u],topf);
for(re int i=head[u];i;i=nxt[i]){
int v=to[i];
if(v==fa[u]||v==son[u])continue;
dfs2(v,v);
}
}
inline int lca(int x,int y){
while(top[x]!=top[y]){
if(dep[top[x]]<dep[top[y]])swap(x,y);
x=fa[top[x]];
}
return dep[x]<dep[y]?x:y;
}
}
using namespace Tree_chain_partition;
template<typename T>
inline void read(T &x){
x=0;T f=1;char ch=getchar();
while (!isdigit(ch)) {if(ch=='-')f=-1;ch=getchar();}
while (isdigit(ch)){x=x*10+(ch^48);ch=getchar();}
x*=f;
}
inline void init(){
read(n),read(m),read(q);
block=pow(n,(double)2/(double)3);
for(re int i=1;i<=n<<1;i++){
belong[i]=(i-1)/block+1;
}
for(re int i=1;i<=m;i++){
read(V[i]);
}
for(re int i=1;i<=n;i++){
read(W[i]);
}
for(re int i=1,u,v;i<n;i++){
read(u),read(v);
add(u,v);add(v,u);
}
for(re int i=1;i<=n;i++){
read(C[i]);
}
dfs1(1,0);
dfs2(1,1);
}
signed main() {
#ifdef LawrenceSivan
freopen("aa.in","r", stdin);
freopen("aa.out","w", stdout);
#endif
init();
for(re int i=1,op;i<=q;i++){
read(op);
if(op==0){
read(modi[++cntm].pos);
read(modi[cntm].val);
}
if(op==1){
int x,y;
read(x),read(y);
if(st[x]>st[y])swap(x,y);
int LCA=lca(x,y);
mocap[++cntq].id=cntq,mocap[cntq].pre=cntm;
if(LCA==x)mocap[cntq].l=st[x],mocap[cntq].r=st[y];
else mocap[cntq].l=ed[x],mocap[cntq].r=st[y],mocap[cntq].lca=LCA;
}
}
sort(mocap+1,mocap+1+cntq);
for(re int i=1;i<=cntq;i++){
while(l>mocap[i].l)calc(pot[--l]);
while(l<mocap[i].l)calc(pot[l++]);
while(r>mocap[i].r)calc(pot[r--]);
while(r<mocap[i].r)calc(pot[++r]);
while(tim<mocap[i].pre)update(++tim);
while(tim>mocap[i].pre)update(tim--);
if(mocap[i].lca)calc(mocap[i].lca);
ans[mocap[i].id]=sum;
if(mocap[i].lca)calc(mocap[i].lca);
}
for(re int i=1;i<=cntq;i++){
printf("%lld\n",ans[i]);
}
return 0;
}
回滚莫队(不删除莫队(少删除莫队))
首先这个玄学的名字是从题解里看到的。
这个题让我们求的玩意就非常诡异。
给定一个序列,多次询问一段区间 \([l,r]\),求区间中相同的数的最远间隔距离。
序列中两个元素的间隔距离指的是两个元素下标差的绝对值。
对于普通的莫队操作,一般是需要支持增加和修改两种操作。
可是有这样的一类题目,在你进行完移动操作以后需要立即更新答案(例如本题)
于是可以发现一个问题:在删除左侧以后,我们需要知道次左,然后又需要知道次左的次左……
于是这玩意就直接凉了。
于是有这么个玩意名字叫回滚莫队,就可以解决这样的问题。
既然我们删除操作不好搞,那我们就不删除!(或者是少删除(这也是不删除莫队名字的由来))
就是说要用增加来代替删除操作。
右端点的增加很好说,我们在排序的时候已经保证右端点有序。
于是就是左端点的问题了。
我们可以把左指针强行拉到右端点,然后让左指针往左走。然后再拉回右端点,然后再往左走。
记录答案只需要先算一算右边的答案,然后再算一算左边的( \(add()\) )
然后算完以后我们就把左端点拉回来,然后把左边的贡献删掉就行了。
本题
我们记左指针为 \(l\),右指针为 \(r\),当前块的右边界(分界线)为 \(mid\), \([l,mid]\) 为左区间,\([mid,r]\) 为右区间
然后答案会有三种情况出现:
-
答案完全在左区间中
-
答案完全在右区间中
-
答案一部分在左区间中,一部分在右区间中
首先答案的右端点是单调的,因此取个 \(\max\) 即可,与当前扫到的下标相减就解决了情况 \(1\) 和 \(3\),
对于情况 \(2\),我们要额外记录一个值,记录一个数在右区间中第一次出现的位置
假如 \(max\) 也在右区间中,相减,就得到了情况2的答案。
细节相关
\(1\):如果左右边界都在同一个块内就暴力计算
int calc(int l,int r){
int last[maxn],res=0;
for(re int i=l;i<=r;i++)last[a[i]]=0;
for(re int i=l;i<=r;i++){
if(!last[a[i]])last[a[i]]=i;
else res=max(res,i-last[a[i]]);
}
return res;
}
\(2\):本题需要离散化
inline void Discretization(){
sort(num+1,num+1+n);
int tmp=unique(num+1,num+1+n)-num-1;
for(re int i=1;i<=n;i++)a[i]=lower_bound(num+1,num+1+tmp,a[i])-num;
}
\(3\) :由于回滚的原因,所以现在的左询问一定是小于上一次的左询问,现在的右询问一定大于上一次的右询问,所以原来莫队的四个 \(while\) 只剩下了两个
while(r<mocap[i].r){
r++;mr[a[r]]=r;
if(!ml[a[r]])ml[a[r]]=r;
ans=max(ans,r-ml[a[r]]);
}
while(l>mocap[i].l){
l--;
if(mr[a[l]])ans=max(ans,mr[a[l]]-l);
else mr[a[l]]=l;
}
Ans[mocap[i].id]=ans;
\(4\):最后不要忘记把左端点再拉回来:
同时有这样一个问题,再左端点走过去的时候,会影响贡献,又因为我们每次都要把左端点拉回最右侧,所以这个贡献对以后的询问是没什么用的,于是我们需要先记录一下当前的答案,再统计完左侧,记录完答案以后,把左端点拉回最右侧的时候去掉左侧的贡献,再把 \(ans\) 更新回来就好了。
while(l<=nowr){
if(mr[a[l]]==l)mr[a[l]]=0;
l++;
}
int tmp=ans;//在l,r之间
ans=tmp;//把左端点拉回来以后
\(5\):其实还有一个细节,就是 \(memset\) 也许会影响常数大小,于是我们不必要每次清空整个数组,只需要记录每次更改了哪些就可以了。
最后再把这些清零就行了。
for(){
while(r<q[i].r){
r++;
mr[a[r]]=r;
if(!st[a[r]]) st[a[r]]=r,clear[++cn]=a[r]; //就是这里
ans=max(ans,r-st[a[r]]);
}
}
for(int i=1;i<=cn;i++) ma[clear[i]]=st[clear[i]]=0;//在大循环外
不过我没用,其实 \(memset\) 的常数并不算太大,常数瓶颈并不在这里。确信
细节大概就这么多了。
CODE:
//#define LawrenceSivan
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
#define re register
const int maxn=2e5+5;
#define INF 0x3f3f3f3f
int n,m,block,tot,ans;
int a[maxn],num[maxn],belong[maxn],Ans[maxn];
int ml[maxn],mr[maxn];//ml是最早出现的位置,mr是最晚出现的位置
int nowr,l,r;
struct MOCAP{
int l,r,id;
inline bool operator <(const MOCAP &a)const{
return belong[l]==belong[a.l]?r<a.r:belong[l]<belong[a.l];
}
}mocap[maxn];
inline void Discretization(){
sort(num+1,num+1+n);
int tmp=unique(num+1,num+1+n)-num-1;
for(re int i=1;i<=n;i++)a[i]=lower_bound(num+1,num+1+tmp,a[i])-num;
}
int calc(int l,int r){
int last[maxn],res=0;
for(re int i=l;i<=r;i++)last[a[i]]=0;
for(re int i=l;i<=r;i++){
if(!last[a[i]])last[a[i]]=i;
else res=max(res,i-last[a[i]]);
}
return res;
}
inline int read(){
int x=0,f=1;char ch=getchar();
while(!isdigit(ch)){if(ch=='-')f=-1;ch=getchar();}
while(isdigit(ch)){x=x*10+(ch^48);ch=getchar();}
return x*f;
}
int main(){
#ifdef LawrenceSivan
freopen("aa.in","r",stdin);
freopen("aa.out","w",stdout);
#endif
n=read();
block=sqrt(n);
for(re int i=1;i<=n;i++){
a[i]=num[i]=read();
belong[i]=(i-1)/block+1;
}
tot=belong[n];
Discretization();
m=read();
for(re int i=1;i<=m;i++){
mocap[i].l=read();mocap[i].r=read();
mocap[i].id=i;
}
sort(mocap+1,mocap+1+m);
for(re int j=1,i=1;j<=tot;j++){
int nowr=min(n,j*block),l=nowr+1,r=l-1,ans=0;
memset(ml,0,sizeof(ml));
memset(mr,0,sizeof(mr));
for(;belong[mocap[i].l]==j;i++){
if(belong[mocap[i].r]==j){
Ans[mocap[i].id]=calc(mocap[i].l,mocap[i].r);
continue;
}
while(r<mocap[i].r){
r++;mr[a[r]]=r;
if(!ml[a[r]])ml[a[r]]=r;
ans=max(ans,r-ml[a[r]]);
}
int tmp=ans;
while(l>mocap[i].l){
l--;
if(mr[a[l]])ans=max(ans,mr[a[l]]-l);
else mr[a[l]]=l;//最后出现的位置可能在左区间中
}
Ans[mocap[i].id]=ans;
while(l<=nowr){
if(mr[a[l]]==l)mr[a[l]]=0;
l++;
}
ans=tmp;
}
}
for(re int i=1;i<=m;i++){
printf("%d\n",Ans[i]);
}
return 0;
}
例题 AT1219 歴史の研究
首先这个题比上一个好写一些
但是作为一个菜鸡还是调了很久。
总结了以下槽点:
\(1\):这个题依然要离散化。
离散化完了以后千万别忘记你已经离散化了!!!
不要傻乎乎的再使用原来的数据了
这充分说明我是个傻逼,这么低级的错误也能犯
\(2\):这个题要开 \(long \ long\)
开了 \(int\) 然后 \(WA\) 了,百思不得其解,然后发现要 \(long \ long\)
好了其实别的几乎没有了,都是我比较傻逼
代码放这了
CODE:
//#define LawrenceSivan
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
#define re register
const int maxn=1e5+5;
#define INF 0x3f3f3f3f
#define int long long
int n,m,block,tot;
int a[maxn],num[maxn],ans[maxn],belong[maxn];
int c[maxn];
inline void Discretization(){
sort(num+1,num+1+n);
int tmp=unique(num+1,num+1+n)-num-1;
for(re int i=1;i<=n;i++)a[i]=lower_bound(num+1,num+1+tmp,a[i])-num;
}
struct MOCAP{
int l,r,id;
inline bool operator < (const MOCAP &a)const{
return belong[l]==belong[a.l]?r<a.r:belong[l]<belong[a.l];
}
}mocap[maxn];
inline int calc(int l,int r){
int res=0;
int cntt[maxn];
for(re int i=l;i<=r;i++){
cntt[a[i]]=0;
}
for(re int i=l;i<=r;i++){
cntt[a[i]]++;
res=max(res,cntt[a[i]]*num[a[i]]);
}
return res;
}
inline int read(){
int x=0,f=1;char ch=getchar();
while(!isdigit(ch)){if(ch=='-')f=-1;ch=getchar();}
while(isdigit(ch)){x=x*10+(ch^48);ch=getchar();}
return x*f;
}
signed main(){
#ifdef LawrenceSivan
freopen("aa.in","r",stdin);
freopen("aa.out","w",stdout);
#endif
n=read();m=read();
block=sqrt(n);
for(re int i=1;i<=n;i++){
a[i]=num[i]=read();
belong[i]=(i-1)/block+1;
}
tot=belong[n];
Discretization();
for(re int i=1;i<=m;i++){
mocap[i].l=read();mocap[i].r=read();
mocap[i].id=i;
}
sort(mocap+1,mocap+1+m);
for(re int j=1,i=1;j<=tot;j++){
int nowr=min(n,j*block),l=nowr+1,r=l-1,sum=0;
memset(c,0,sizeof(c));
for(;belong[mocap[i].l]==j;i++){
if(belong[mocap[i].r]==j){
ans[mocap[i].id]=calc(mocap[i].l,mocap[i].r);
continue;
}
while(r<mocap[i].r){
r++;
c[a[r]]++;
sum=max(sum,c[a[r]]*num[a[r]]);
}
int tmp=sum;
while(l>mocap[i].l){
l--;
c[a[l]]++;
sum=max(sum,c[a[l]]*num[a[l]]);
}
ans[mocap[i].id]=sum;
while(l<=nowr){
c[a[l]]--;
l++;
}
sum=tmp;
}
}
for(re int i=1;i<=m;i++){
printf("%lld\n",ans[i]);
}
return 0;
}
变式 Rmq Problem / mex
后来我在智能推荐里找到了这道题。
一眼看上去这个题面,貌似之前讲过的。
之前讲的是可持久化线段树的做法。
但是现在发现这玩意还可以用回滚莫队来搞。
不过做了这道题确实颠覆和加深了我对回滚莫队的认识。
题目很简洁:求给定区间内没有出现的最小的自然数是多少。
稍加思考可以发现,这个东西的加入操作是没有办法做到 \(O(1)\) 的。
比如目前有一个序列:\(0,6,3,5,4,2\) ,现在没有出现的最小自然数是 \(1\)。
如果随着查询端点的移动,下一个位置要加入的数字恰好是 \(1\),那么现在这个区间就出现 \(1\) 了,于是我们要统计最小没有出现过的自然数的话就要从新统计。
这是不好的。
反观删除操作,如果还是上面的例子,现在右端点收缩,\(2\) 就会被删除,于是我们只需要比较一下 \(2,1\) 的大小关系,就可以在 \(O(1)\) 的时间内确定新的 \(mex\).
这启示我们需要使用一个只资瓷删除而不资瓷增加的莫队。
而根据我们刚刚学回滚莫队所联想的只资瓷增加不资瓷删除的回滚莫队相类比,我们可以将每个块按照左端点递增排序,右端点递减排序。
首先求出整个序列的 \(mex\).
然后我们让右端点从整个序列的右侧不断地向左删除,同时左端点向右删除,处理完了以后我们让左端点回滚到块的左端点。这样就可以实现了。
struct MOCAP{
int l,r,id;
inline bool operator <(const MOCAP &a)const{
return belong[l]==belong[a.l]?r>a.r:belong[l]<belong[a.l];
}
}mocap[maxn];
可以画个图理解一下:
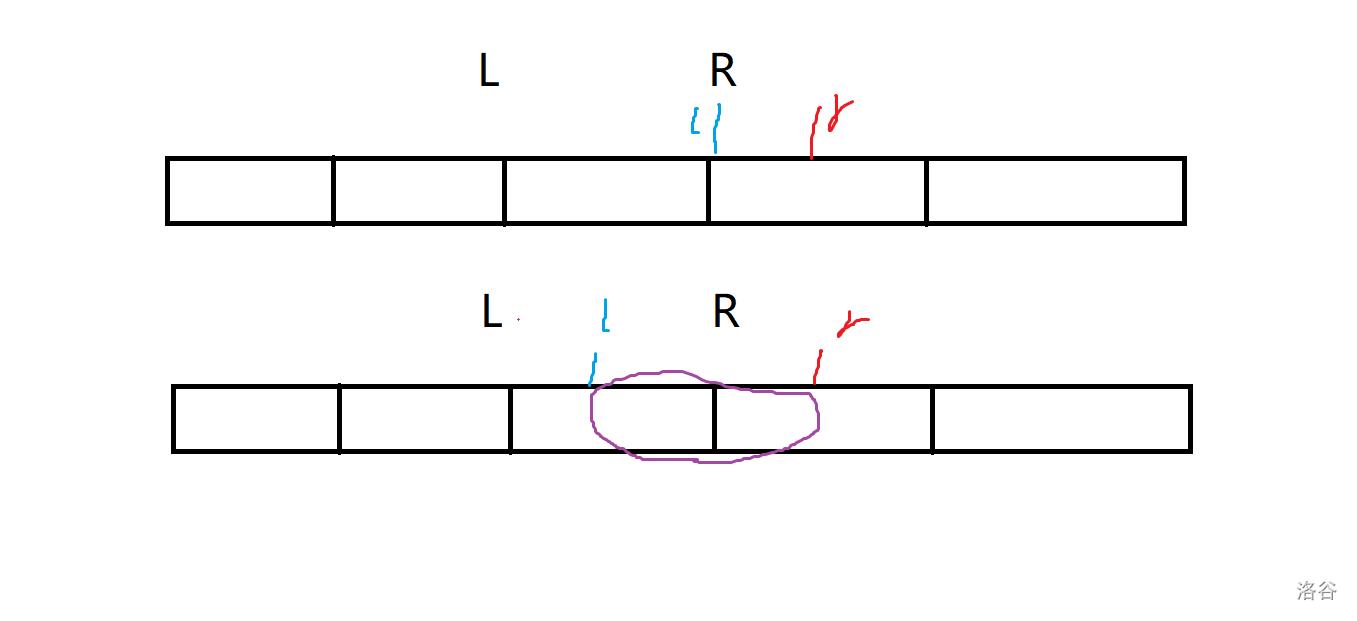
这个是普通的回滚莫队
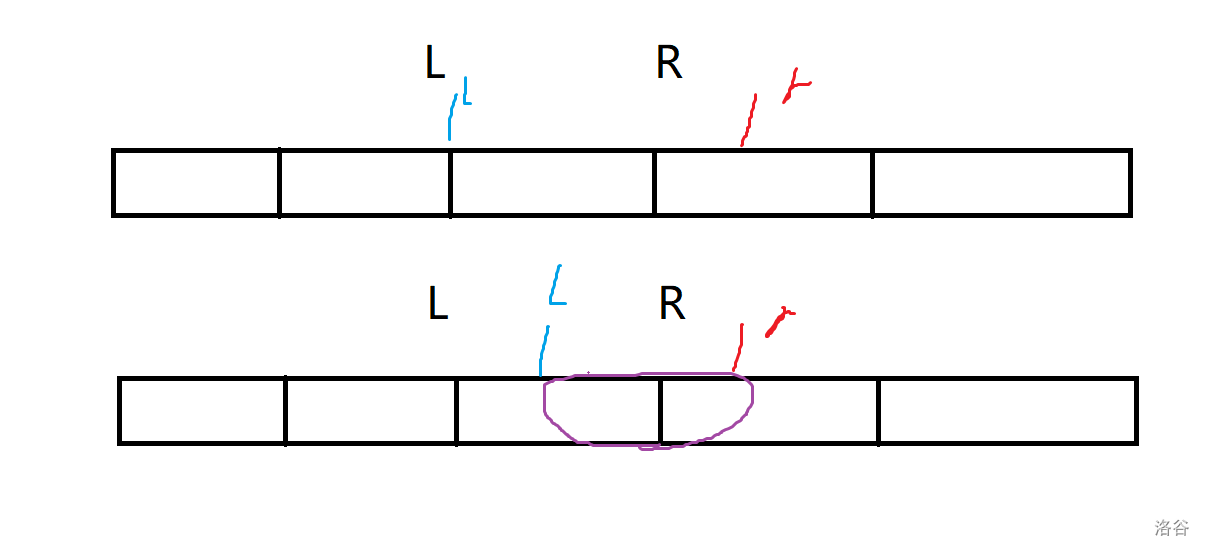
这个是只减不增的回滚莫队
处理完一个块的询问之后,左指针必然会回滚到块的左端点
这时,类似只加不减的回滚莫队,先暴力地把右指针遍历到整个序列的最右端,然后左指针向右删除到下一个块的左端点。
细节相关:
贡献与端点移动的先后关系:
之前我们写的回滚莫队是只增不减的,现在的是只减不增的。
- 在只增不减的回滚莫队中:
我们已经处理过当前询问内的贡献,现在需要扩大范围,但是当前的贡献也要保留,所以应该先跳动端点指针,然后再增加贡献:
while(r<mocap[i].r){
r++;
c[a[r]]++;
sum=max(sum,c[a[r]]*num[a[r]]);
}
while(l>mocap[i].l){
l--;
c[a[l]]++;
sum=max(sum,c[a[l]]*num[a[l]]);
}
(这两个片段是歴史の研究里面的)
- 在只减不增的回滚莫队中:
再来看这道题,只删除不增加:
我们需要缩小范围,也就是要逐个删除贡献,于是当前位置的贡献已经没有用了,所以要先删掉,才能移动指针去修改下一个位置:
while(r>mocap[i].r){
if(a[r]<=n+1&&!--cnt[a[r]])p=min(p,a[r]);
r--;
}
while(l<mocap[i].l){
if(a[l]<=n+1&&!--cnt[a[l]])tmp=min(tmp,a[l]);
l++;
}
关于左右端点的位置记录与移动
因为以往的回滚都是要回到当前块的右端点,所以我们每次只记录右端点就可以了,但是这道题是要回到左端点,所以需要记录左端点。
处理完一个块以后,我们要控制左端点移动到下一个快的左端点,所以这些问题都要注意:
int nowr=min(n,j*block),l=nowr+1,r=l-1,sum=0;
(依然是歴史の研究里面的)
int nowl=min(n,(j-1)*block)+1,l=nowl,r=n,p=mex,nxtl=min(n,j*block)+1;
(本题目)
而且要注意,我们的右端点是要从整个序列的右端开始走的,所以要 \(r=n\) .
然后就是把右端点拉回最右侧,左端点拉到下一个块,这个东西也是平常的回滚莫队没有的:
while(r<n){
r++;
if(a[r]<=n+1)cnt[a[r]]++;
}
while(l<nxtl){
if(a[l]<=n+1&&!--cnt[a[l]])mex=min(mex,a[l]);
l++;
}
关于在同一个块内的暴力计算
首先这个东西有两种实现方法;
\(1\):开一个全局数组,每次暴力算就先用一用,然后统计完再把贡献删掉:
if(belong[mocap[i].r]==j){
int res=0;
for(re int k=mocap[i].l;k<=mocap[i].r;k++){
if(a[k]<=n+1)cntt[a[k]]++;
}
while(cntt[res])res++;
ans[mocap[i].id]=res;
for(re int k=mocap[i].l;k<=mocap[i].r;k++){
if(a[k]<=n+1)cntt[a[k]]--;
}
continue;
}
但是我不喜欢。
如果你和我一样,都喜欢单独搞一个函数,然后在函数里直接统计,这样就可以不删除贡献了,用完就可以扔了。可以不负责的感觉好爽
但是一定要记得初始化!!
不然你会 \(WA\) 的很惨~
inline int calc(int l,int r){
int res=0,cntt[maxn];
memset(cntt,0,sizeof(cntt));
for(re int i=l;i<=r;i++){
if(a[i]<=n+1)cntt[a[i]]++;
}
while(cntt[res])res++;
return res;
}
其他问题就没啥可说的了。
放下代码
CODE:
//#define LawrenceSivan
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
#define INF 0x3f3f3f3f
#define re register
const int maxn=2e5+5;
int n,m,belong[maxn],block,tot;
int cnt[maxn],mex,ans[maxn];
int a[maxn];
struct MOCAP{
int l,r,id;
inline bool operator <(const MOCAP &a)const{
return belong[l]==belong[a.l]?r>a.r:belong[l]<belong[a.l];
}
}mocap[maxn];
inline int calc(int l,int r){
int res=0,cntt[maxn];
memset(cntt,0,sizeof(cntt));
for(re int i=l;i<=r;i++){
if(a[i]<=n+1)cntt[a[i]]++;
}
while(cntt[res])res++;
return res;
}
inline int read(){
int x=0, f=1;char ch=getchar();
while (!isdigit(ch)) {if(ch=='-')f=-1;ch=getchar();}
while (isdigit(ch)){x=x*10+(ch^48);ch=getchar();}
return x*f;
}
int main() {
#ifdef LawrenceSivan
freopen("aa.in", "r", stdin);
freopen("aa.out", "w", stdout);
#endif
n=read();m=read();
block=sqrt(n);
for(re int i=1;i<=n;i++){
a[i]=read();
belong[i]=(i-1)/block+1;
if(a[i]<=n+1)cnt[a[i]]++;
}
while(cnt[mex])mex++;
tot=belong[n];
for(re int i=1;i<=m;i++){
mocap[i].l=read();mocap[i].r=read();
mocap[i].id=i;
}
sort(mocap+1,mocap+1+m);
for(re int i=1,j=1;j<=tot;j++){
int nowl=min(n,(j-1)*block)+1,l=nowl,r=n,p=mex,nxtl=min(n,j*block)+1;
for(;belong[mocap[i].l]==j;i++){
if(belong[mocap[i].r]==j){
ans[mocap[i].id]=calc(mocap[i].l,mocap[i].r);
continue;
}
while(r>mocap[i].r){
if(a[r]<=n+1&&!--cnt[a[r]])p=min(p,a[r]);
r--;
}
int tmp=p;
while(l<mocap[i].l){
if(a[l]<=n+1&&!--cnt[a[l]])tmp=min(tmp,a[l]);
l++;
}
ans[mocap[i].id]=tmp;
while(l>nowl){
l--;
if(a[l]<=n+1)cnt[a[l]]++;
}
}
while(r<n){
r++;
if(a[r]<=n+1)cnt[a[r]]++;
}
while(l<nxtl){
if(a[l]<=n+1&&!--cnt[a[l]])mex=min(mex,a[l]);
l++;
}
}
for(re int i=1;i<=m;i++){
printf("%d\n",ans[i]);
}
return 0;
}

 莫队
莫队

 浙公网安备 33010602011771号
浙公网安备 33010602011771号