UVA12558 埃及分数 Egyptian Fractions (HARD version)（迭代加深搜索）

迭代加深搜索

在搜索问题中，有一些问题，搜索树不仅每一层宽度很广，而且深度很大，

于是我们只用bfs和dfs的缺点就十分明显，只用bfs我们也许会陷入一层而迟迟进不去下一层，

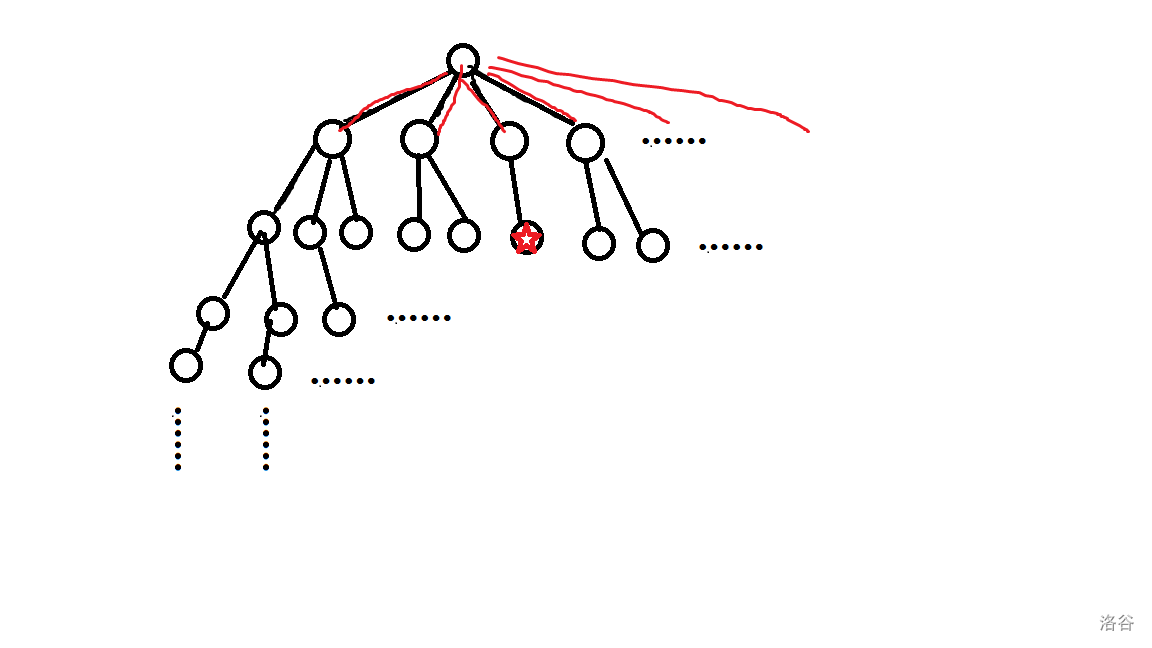
用dfs就会导致一直深入递归某一棵子树而无法进入其他子树，

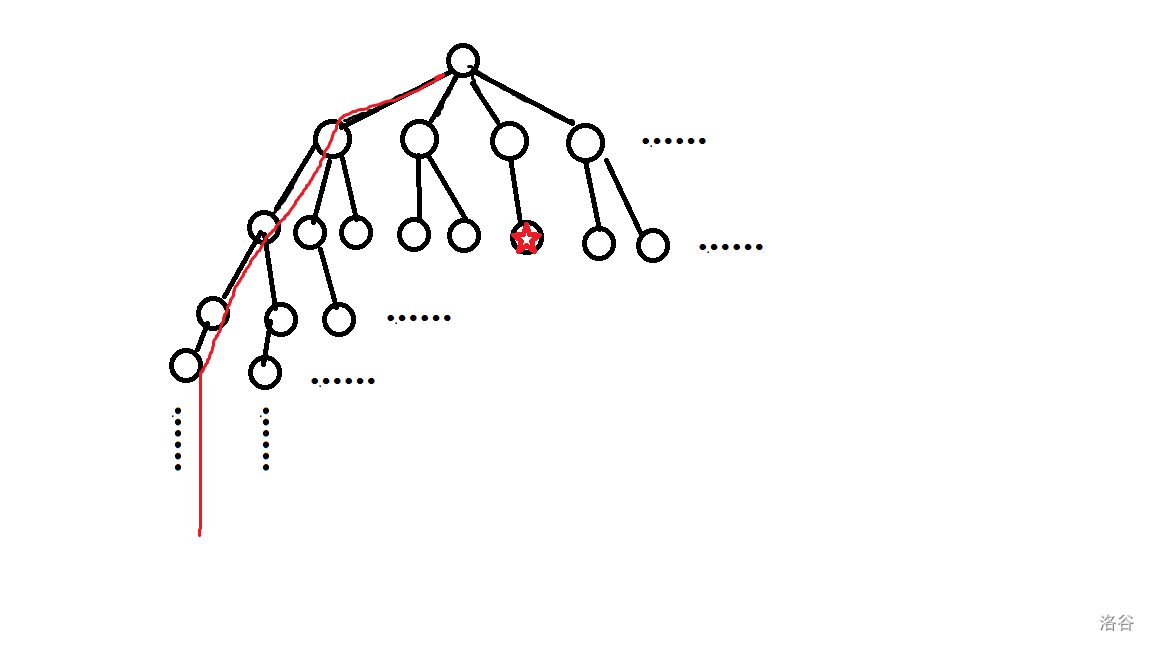
于是我们就可以考虑迭代加深搜索，就是说我们先限制一个范围，在我们限制的范围中进行求解，如果无法得出问题的解我们就扩大范围。

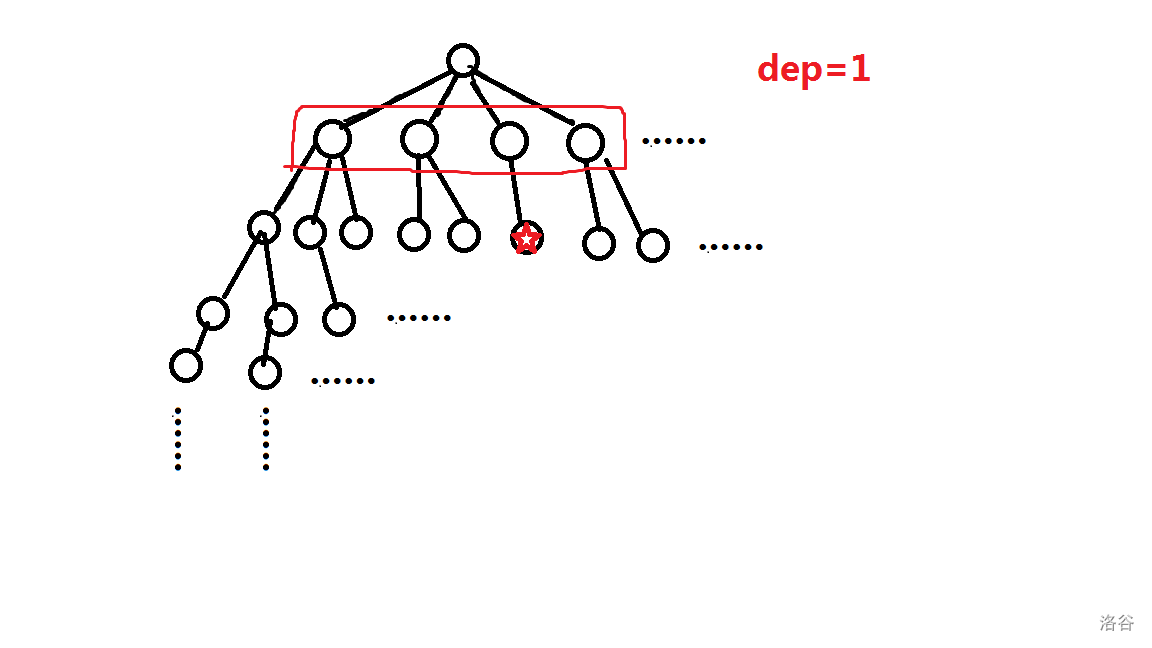
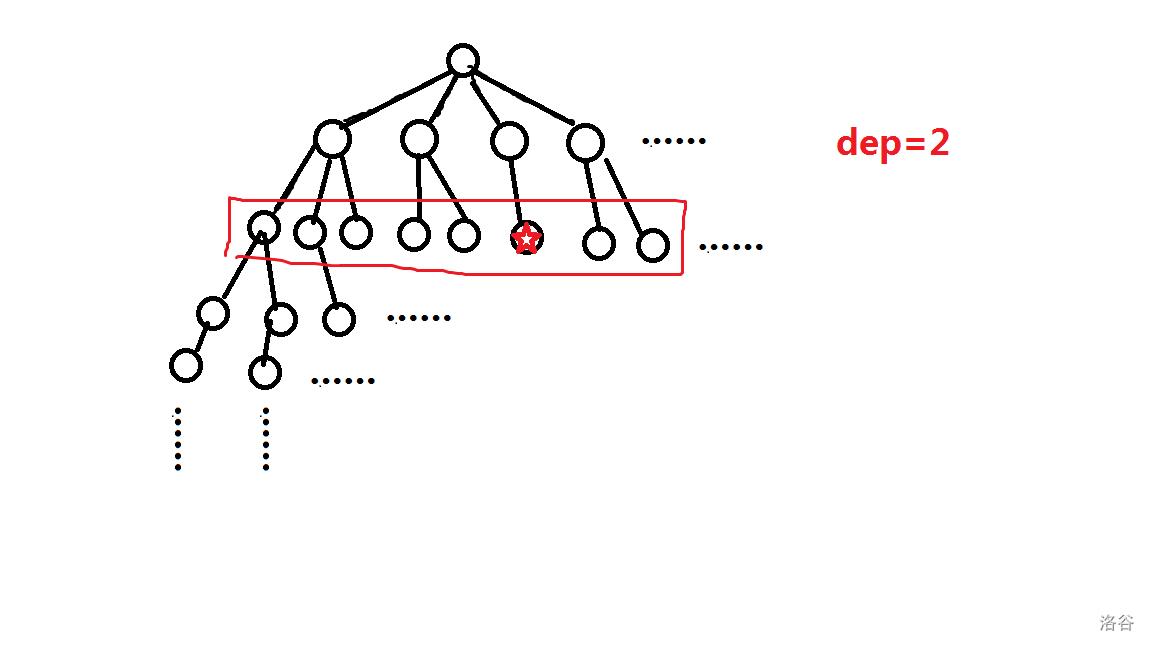
这就是迭代加深的思想。

下面看一道例题：

UVA12558 埃及分数 Egyptian Fractions (HARD version)

题面：传送门

本题中没有分数个数和分母的上限，所以我们可以发现这就是一个无上限的搜索问题，于是考虑迭代加深搜索

注意到题目中给出了限制条件，即部分数字是不可以用的，于是我们可以考虑使用set来判重。

//#define LawrenceSivan

#include<bits/stdc++.h>
using namespace std;

typedef long long ll;
#define re register

int num,T,t,k;
ll h[100001],ans[100001],a,b,q;
set <ll> del;
bool ok;

inline void init(){
	del.clear();
	ok=0;
}

inline ll mmax(ll a,ll b){
	return a>b?a:b;
}

inline ll gcd(ll a,ll b){
	return b==0?a:gcd(b,a%b);
}

inline bool better(){
    for(int i=num;i>=0;--i)
        if(h[i]!=ans[i])
            return ans[i]==-1||h[i]<ans[i];
    return 0;
}

inline void dfs(ll p1,ll p2,int last,int cnt){//p1·Ö×Ó  p2·Öĸ  last:Õâ´Î´ÓÄĸö·Öĸ¿ªÊ¼ËÑ cnt:ÒѾ­Ìí¼ÓÁ˼¸¸ö·ÖÊý
    if(cnt==num){
        if(p2%p1||del.count(p2/p1))return;//·Ö×Ó²»Îª1»òÕßÕâ¸öÊý±»½ûÖ¹³öÏÖ
        h[cnt]=p2;ok=1;
        if(better())memcpy(ans,h,sizeof(ll)*(cnt+1));//¸üÐÂ×îÓŽâ
        return;
    }
    for(ll i=mmax(last,p2/p1+1);;++i){ // p2/p1+1:·ûºÏÌõ¼þµÄ×îС·Öĸ£¬ÓÃÓÚ¼ôÖ¦
    	if(p1*i>=p2*(num-cnt+1))break; //·¢ÏÖ×îºó¼õ²»ÍêÁË£¬Ìø³ö
        if(del.count(i))continue;
        ll q1=p1*i-p2,q2=p2*i,G=gcd(q1,q2); //ͨ·Ö
        h[cnt]=i;
        dfs(q1/G,q2/G,i+1,cnt+1);
    }
}

template <typename T>
inline T read(){
	T x=0,f=1;char ch=getchar();
	while(!isdigit(ch)){if(ch=='-')f=-1;ch=getchar();}
	while(isdigit(ch)){x=x*10+(ch^48);ch=getchar();}
	return x*f;
}

int main(){
#ifdef LawrenceSivan
	freopen("aa.in","r",stdin);
	freopen("aa.out","w",stdout);
#endif 

    T=read<int>();
    
    while(T--){
    	init();
    	
        a=read<ll>();b=read<ll>();k=read<int>();
        
        for(re int i=1;i<=k;++i){
        	q=read<ll>();
			del.insert(q);
		}
        
		for(num=1;!ok;++num){//ÿ´ÎÏÞÖƲãÊý 
            memset(ans,-1,sizeof(ans));
            dfs(a,b,b/a+1,0);
        }
        
		--num; //×¢ÒâÒª¼õµô¶à³öµÄÒ»´Î++num²Ù×÷
        printf("Case %d: %lld/%lld=",++t,a,b);
        
        for(int i=0;i<num;++i){
        	printf("1/%lld+",ans[i]);
		}
        printf("1/%lld\n",ans[num]);
        
	}
        
    return 0;
}