Codeforces Round #600 (Div. 2) [A-E]

目录

• Codeforces Round #600 (Div. 2)
  • A. Single Push
    • 思路
    • Code
  • B. Silly Mistake
    • 思路
    • Code
  • C. Sweets Eating
    • 思路
    • Code
  • D. Harmonious Graph
    • 思路
      • Solution1
      • Solution2
    • Code
  • E. Antenna Coverage
    • 思路
    • Code
  • 后记

Codeforces Round #600 (Div. 2)

A. Single Push

思路

你可以进行最多一次操作：选择三个数\(l, r, k\)，且\(1\le l\le r\le n\)且\(k>0\)。使得\(a\)数组可以转化为\(b\)数组。

Note: \(n \le 100\;000\)

数形结合。

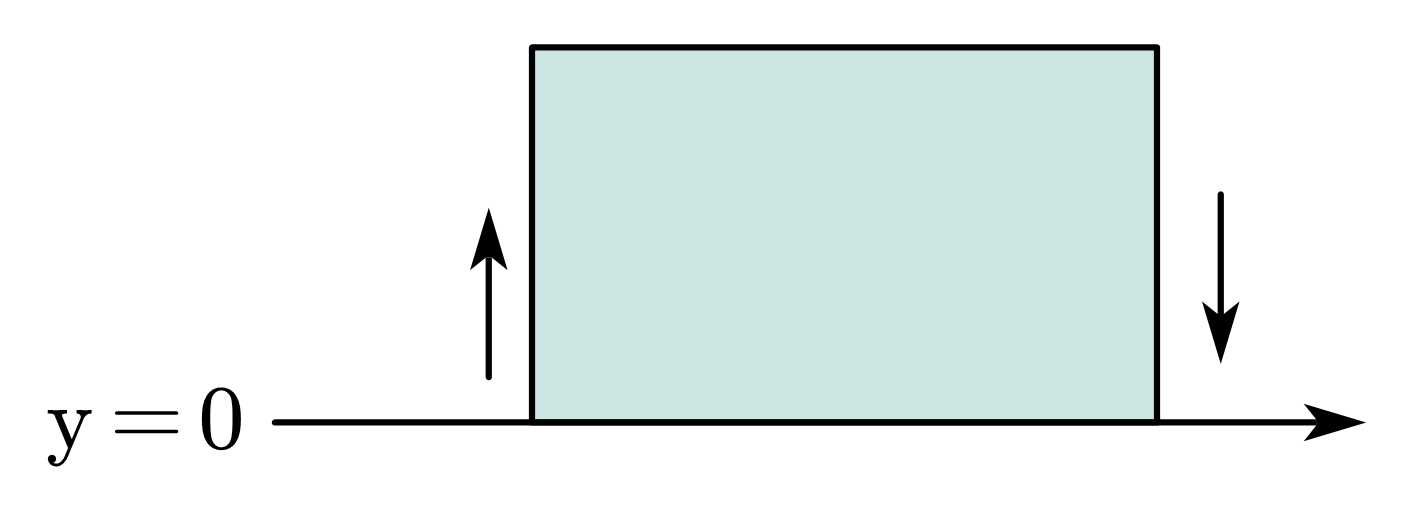
做a与b的差分。由图可知在边界左右均为0的情况下，最多有两次差别。

Code

#include <bits/stdc++.h>
using namespace std;
#define DEBUG 0

// #define int long long
#define pb push_back
#define vt std::vector
#define lb lower_bound
#define sz(x) (int(x.size()))
#define all(x) x.begin(), x.end()
#define mst(x, bit) memset(x, bit, sizeof(x))
#define rep(i, l, r) for (ll i = (l); i < (r); ++ i)
#define forr(i, l, r) for (ll i = (l); i >= (r); -- i)
#define dmp(x) cerr << __LINE__ << "->" << #x << " " << x << "\n"

using ll = long long;
using db = double;
using pii = pair<int, int>;
using pll = pair<ll, ll>;

template<typename... Args>
inline void wpr(Args... args) { std::cout << '\n'; }
template<typename T, typename... Args>
void wpr(T val, Args... args) { std::cout << val << " "; wpr(args...); }

const int maxn = 1e5 + 50;
const int inf = 0x3f3f3f3f;

void solve(){
    int n; 
    std::cin >> n;
    vt<int> a(n), b(n), dlt(n + 2, 0);
    rep (i, 0, n) std::cin >> a[i];
    rep (i, 0, n) std::cin >> b[i];
    rep (i, 0, n) dlt[i + 1] = b[i] - a[i];

    // 数形结合，绘图可以发现，左右边界都为 0，此时保证只有两个波动。
    int cnt = 0;
    rep (i, 1, n + 2){
        if (dlt[i] < 0) { wpr("no"); return; }
        if (dlt[i] != dlt[i - 1]) ++ cnt;
    }

    if (cnt <= 2) wpr("yes");
    else wpr("no");
}

signed main(){
    ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
    int t = 1;
    std::cin >> t;
    while (t--) solve();
    return 0;
}

B. Silly Mistake

思路

设整数\(x\)，当其为正数时认为其进入办公室，当其为负数时认为其出办公室。一个人一天最多进一次，且不能在没进来前出去。每天结束时办公室没人。请你将一个序列\(a\)划分为多天保证每天都是合法的。

Note: \(n\le100\;000;-1e6\le a_i \le 1e6\)

对于每个people定义三个状态：(利用const int定义，学到了。)

• WAIT 代表等待有人进入。
• COME 代表已经有人进入。
• LEFT 代表人已经出去了。

同时我们定义ofs代表办公室的人数，利用贪心的想法，每次ofs == 0时便结束一天。基于该思想判断是否合法，请注意新的一天需要你清空状态。

Code

#include <bits/stdc++.h>
using namespace std;
#define DEBUG 0

// #define int long long
#define pb push_back
#define vt std::vector
#define lb lower_bound
#define sz(x) (int(x.size()))
#define all(x) x.begin(), x.end()
#define mst(x, bit) memset(x, bit, sizeof(x))
#define rep(i, l, r) for (ll i = (l); i < (r); ++ i)
#define forr(i, l, r) for (ll i = (l); i >= (r); -- i)
#define dmp(x) cerr << __LINE__ << "->" << #x << " " << x << "\n"

using ll = long long;
using db = double;
using pii = pair<int, int>;
using pll = pair<ll, ll>;

template<typename... Args>
inline void _wpr_(Args... args) { std::cout << '\n'; }
template<typename T, typename... Args>
inline void _wpr_(T val, Args... args) { std::cout << " " << val; _wpr_(args...); }
template<typename T, typename... Args>
void wpr(T val, Args... args) { std::cout << val; _wpr_(args...); }

const int maxn = 1e6 + 50;
const int inf = 0x3f3f3f3f;

const int WAIT = 0, COME = 1, LEFT = 2;
int m[maxn];
void solve(){
    int n; std::cin >> n;

    // ofc means the count of office
    int ofc = 0;

    // cur denote the current array. ans means answer array.
    vt<int> cur, ans;

    rep (i, 0, n){
        int x; std::cin >> x;
        int abx = abs(x);
        cur.pb(abx);

        if (x > 0){
            if (m[abx] != WAIT) { wpr(-1); return; }
            m[abx] = COME;
            ++ ofc;
        }else {
            if (m[abx] != COME) { wpr(-1); return; }
            m[abx] = LEFT;
            -- ofc;
        }

        if (0 == ofc){
            ans.pb(sz(cur));
            for (auto x: cur) m[x] = WAIT;
            cur.clear();
        }

    }

    // if not over, return false. 
    if (!cur.empty()) { wpr(-1); return; }

    std::cout << sz(ans) << "\n";
    rep (i, 0, sz(ans)) std::cout << ans[i] << " \n"[i == sz(ans) - 1];
}

signed main(){
    ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
    int t = 1;
    // std::cin >> t;
    while (t--) solve();
    return 0;
}

C. Sweets Eating

思路

一共有 \(n\) 个糖果，每个糖果浓度为\(a_i\)。一个人每天最多吃\(m\)个糖。在第\(d\)天吃浓度为\(a_k\)的糖的伤害为\(d \cdot a_k\)。请你给出在吃\(k\)糖的情况下的最小伤害。

Note: \(1\le m \le n \le 200\;000; 1\le a_i \le 200\;000\)

显然，策略非常清晰：浓度高的糖果，需要尽可能早的吃。排序即可。

但是，这里涉及到一共分层的问题。

例如：

m = 2

day    add     Δ
 1      f1     0
 2      f2     0
 3      f3     f1
 4      f4     f2
 5      f5     f1 + f3

实际上，这里有一个分层的感觉。这种涉及到分桶，进位的大多可以与模数之间联系。我们分\(m\)个桶，当你新添加第\(j\)天时，由于需要额外增加，会把bucket[j % m]桶中的加到答案中，再进一步更新桶。数很大，注意开long long。

Code

#include <bits/stdc++.h>
using namespace std;
#define DEBUG 0

#define int long long
#define pb push_back
#define vt std::vector
#define lb lower_bound
#define sz(x) (int(x.size()))
#define all(x) x.begin(), x.end()
#define mst(x, bit) memset(x, bit, sizeof(x))
#define rep(i, l, r) for (ll i = (l); i < (r); ++ i)
#define forr(i, l, r) for (ll i = (l); i >= (r); -- i)
#define dmp(x) cerr << __LINE__ << "->" << #x << " " << x << "\n"

using ll = long long;
using db = double;
using pii = pair<int, int>;
using pll = pair<ll, ll>;

template<typename... Args>
inline void wpr(Args... args) { std::cout << '\n'; }
template<typename T, typename... Args>
void wpr(T val, Args... args) { std::cout << val << " "; wpr(args...); }

const int maxn = 1e5 + 50;
const int inf = 0x3f3f3f3f;

void solve(){
    int n, m;
    std::cin >> n >> m;
    vt<int> f(n);
    rep (i, 0, n) {
        std::cin >> f[i];
    }
    sort(all(f));
    ll ans = 0;

    // Layering is related to modulus.
    // Saving the sum of number which have same modulus.
    vt<ll> buck(m + 1, 0);
    rep (k, 0, n){
        ans += f[k];
        ans += buck[k % m];
        buck[k % m] += f[k];
        std::cout << ans << " \n"[k == n - 1];
    }
}

signed main(){
    ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
    int t = 1;
    // std::cin >> t;
    while (t--) solve();
    return 0;
}

D. Harmonious Graph

思路

给定\(n\)个点，\(m\)条边的无向图。假设harmonious的定义是：

• 假如存在\(l\)到\(r\)的路径（\(l < r\))，则存在所有\((l, m) \quad m\in(l, r)\)。

请问，假如希望该图满足harmonious性质，需要增加最少多少个边。

Note: \(3\le n\le200\;000; 1 \le m \le 200\;000\)

Solution1

不难想到将用DSU去处理。假设DSU中的某个连通分量的最小值为lower，最大值为upper。显然，我们需要使得其中所有的点都相互连接，只需要upper - lower + 1 - size(连通分量)。但是，假如我们将其看成区间的形式\([lower, upper]\)，可能存在区间交的情况，我们需要进行区间合并之后再对每个联通分量进行处理。时间复杂度为\(O(m\log n)\)，主要为DSU合并的时间。

但是，通过思考，我们可以发现一个简单的规律。

Solution2

假设DSU中的终极Father永远是连通分量中最大的数。不妨定义\(parent(i) 为 i的源点\)。那么，假如parent(i) > i则说明区间\([i, parent[i]]\) 都需要合并。因此，我们每次合并\((i, i + 1)\)即可，这样我们可以通过一次扫描简单的完成任务。

Code

// for Solution2
#include <bits/stdc++.h>
using namespace std;
#define DEBUG 0

#define int long long
#define pb push_back
#define vt std::vector
#define lb lower_bound
#define sz(x) (int(x.size()))
#define all(x) x.begin(), x.end()
#define mst(x, bit) memset(x, bit, sizeof(x))
#define rep(i, l, r) for (ll i = (l); i < (r); ++ i)
#define forr(i, l, r) for (ll i = (l); i >= (r); -- i)
#define dmp(x) cerr << __LINE__ << "->" << #x << " " << x << "\n"

using ll = long long;
using db = double;
using pii = pair<int, int>;
using pll = pair<ll, ll>;

template<typename... Args>
inline void wpr(Args... args) { std::cout << '\n'; }
template<typename T, typename... Args>
void wpr(T val, Args... args) { std::cout << val << " "; wpr(args...); }

const int maxn = 1e5 + 50;
const int inf = 0x3f3f3f3f;

struct DSU{
    int n, cnt;
    // here mx, mn, tot is useless. There are useful for solution 1
    vt<int> parent, mx, mn, tot;
    void init(int n){
        // 1-index
        this->n = n; cnt = n;
        parent.resize(n + 1), mx.resize(n + 1), mn.resize(n + 1), tot.resize(n + 1);
        for (int i = 0; i <= n; ++ i){
            parent[i] = mx[i] = mn[i] = i;
            tot[i] = 1;
        }
    }

    int find(int x){
        return x == parent[x] ? x : parent[x] = find(parent[x]);
    }

    bool to_union(int x, int y){
        x = find(x);
        y = find(y);
        if (x == y) return false;
        
        -- cnt;
        if (y > x) swap(x, y);
        parent[y] = x;
        tot[x] += tot[y];
        mx[x] = max(mx[x], mx[y]);
        mn[x] = min(mn[x], mn[y]);
        return true;
    }
};



void solve(){
    int n, m;
    std::cin >> n >> m;
    DSU dsu1;
    dsu1.init(n);

    rep (i, 0, m){
        int u, v; std::cin >> u >> v;
        dsu1.to_union(u, v);
    }

    int ans = 0;
    rep (i, 1, n){
        if (dsu1.find(i) <= i) continue;
        ans += dsu1.to_union(i + 1, i);
    }
    wpr(ans);
}

signed main(){
    // ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
    int t = 1;
    // std::cin >> t;
    while (t--) solve();
    return 0;
}

E. Antenna Coverage

思路

给定\(n\)个点，每个点的位置为\(x_i\)能力值为\(s_i\)，其覆盖范围是\([x_i-s_i, x_i+s_i]\)。

你可以通过消耗一枚硬币增加某个点的一个能力值。

给定最大值\(m\)，计算覆盖\([1\cdots m]\)需要的最小硬币数量。

Note:

• \(1\le n \le 80; n \le m \le 100\; 000;\)
• \(1\le x_i \le m; 0\le s_i \le m\)

这题刚开始觉得是E肯定比较难，哪知道很套路。因为\(n\)足够小，我们可以用\(\mathcal{O(n\cdot m)}\)的算法解决。

假设\(dp(i):=完成前i个覆盖的最小值\)。

其状态转移如下：

\[dp(i):= \min \left\{\begin{array}{ll} i & 默认情况 \\ dp[i - 1] + 1 & 在前一共的基础上增加1个硬币 \\ dp[i - 1] & 如果\textbf{本来就被覆盖了} \\ dp[\max(0, x[j] - s[j] - 1 - cost)] + cost & j是x[j]<i的天线，cost是从天线j覆盖到i所需开销 \end{array}\right. \]

Code

#include <bits/stdc++.h>
using namespace std;
#define DEBUG 0

// #define int long long
#define pb push_back
#define vt std::vector
#define lb lower_bound
#define sz(x) (int(x.size()))
#define all(x) x.begin(), x.end()
#define mst(x, bit) memset(x, bit, sizeof(x))
#define rep(i, l, r) for (ll i = (l); i < (r); ++ i)
#define forr(i, l, r) for (ll i = (l); i >= (r); -- i)
#define dmp(x) cerr << __LINE__ << "->" << #x << " " << x << "\n"

using ll = long long;
using db = double;
using pii = pair<int, int>;
using pll = pair<ll, ll>;

template<typename... Args>
inline void _wpr_(Args... args) { std::cout << '\n'; }
template<typename T, typename... Args>
inline void _wpr_(T val, Args... args) { std::cout << " " << val; _wpr_(args...); }
template<typename T, typename... Args>
void wpr(T val, Args... args) { std::cout << val; _wpr_(args...); }

const int maxn = 1e5 + 50;
const int inf = 0x3f3f3f3f;

int dp[maxn];
int can[maxn];
void solve(){
    int n, m; std::cin >> n >> m;

    // fi -> position x, se -> scope
    vt<pii> f;

    // can -> if the position i is include?
    rep (i, 0, n){
        int x, c; std::cin >> x >> c;
        rep (j, max(1, x - c), min(m, x + c) + 1) can[j] = 1;
        f.pb(make_pair(x, c));
    }
    
    dp[0] = 0;
    rep (i, 1, m + 1){
        dp[i] = i;
        if (can[i]) dp[i] = min(dp[i], dp[i - 1]);
        dp[i] = min(dp[i], dp[i - 1] + 1);

        rep (j, 0, n){
            // if it is exceeded, not consider.
            if (f[j].first > i) continue;

            // Len -> cost
            int Len = max(0ll, i - f[j].first - f[j].second);

            // transfrom from (xi - ci - cost - 1)[the left of the point.]
            dp[i] = min(dp[i], dp[max(0, f[j].first - f[j].second - Len - 1)] + Len);
        }   
    }
    wpr(dp[m]);
}

signed main(){
    ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
    int t = 1;
    // std::cin >> t;
    while (t--) solve();
    return 0;
}		

后记

• A: 数形结合，增加dummy node防止边界问题。
• B: 模拟题，贪心考虑。
• C: 和分层有关的考虑模数
• D: 连通分量考虑DSU，考虑遍历优化策略
• E: 多思考dp...