杂谈（11.13——lca && mst)

先放在这 哈哈！

洛谷——P1991 无线通讯网

题目大意

给定 \(p\) 个点的坐标，和 \(s\) 个电话机，按照了电话机的点直接的权为 \(0\) ，问生成树中最大的边为多大。

其中：

• 1<=p<=500
• 1<=s<=100
• 0<=x,y<=10000

思路分析

这题数据量比较小，可以很暴力的把所有点到点之间的边全部存起来，跑一个Kruskal得到最小生成树。

实际上，这是一个求瓶颈树的问题，存在一个结论：最小生成树是瓶颈树的充分不必要条件

也就是，我们直接求最小生成树即可。

求完之后考虑如何安装电话机。

首先，我们考虑 \(s == 2\) 时：

• 显然，这时候我们一定可以把生成树中边权最大的边置 \(0\) ，答案为第二大的边权值：

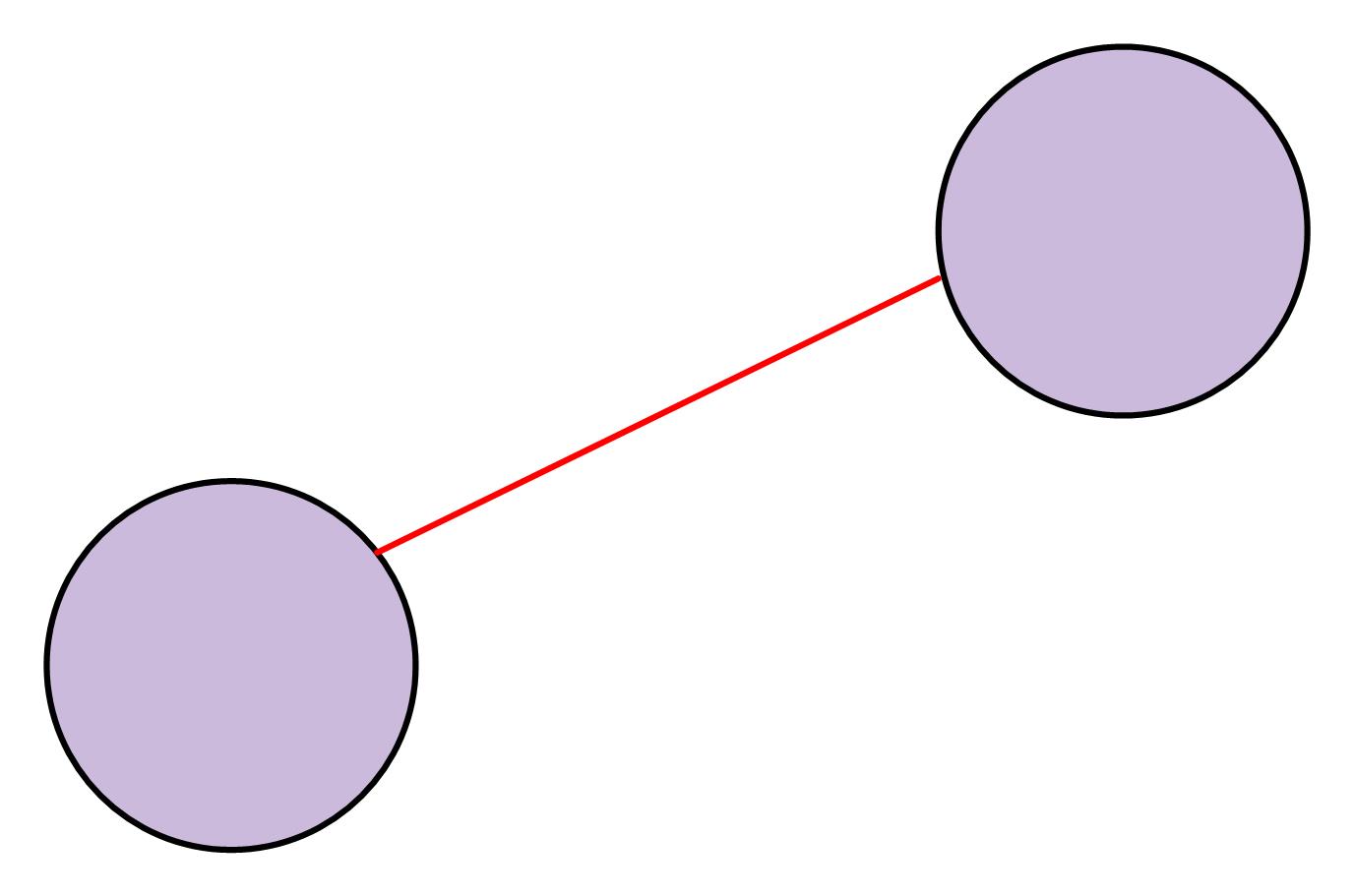
现在我们考虑 \(s == 3\) 的情况：

情况一：

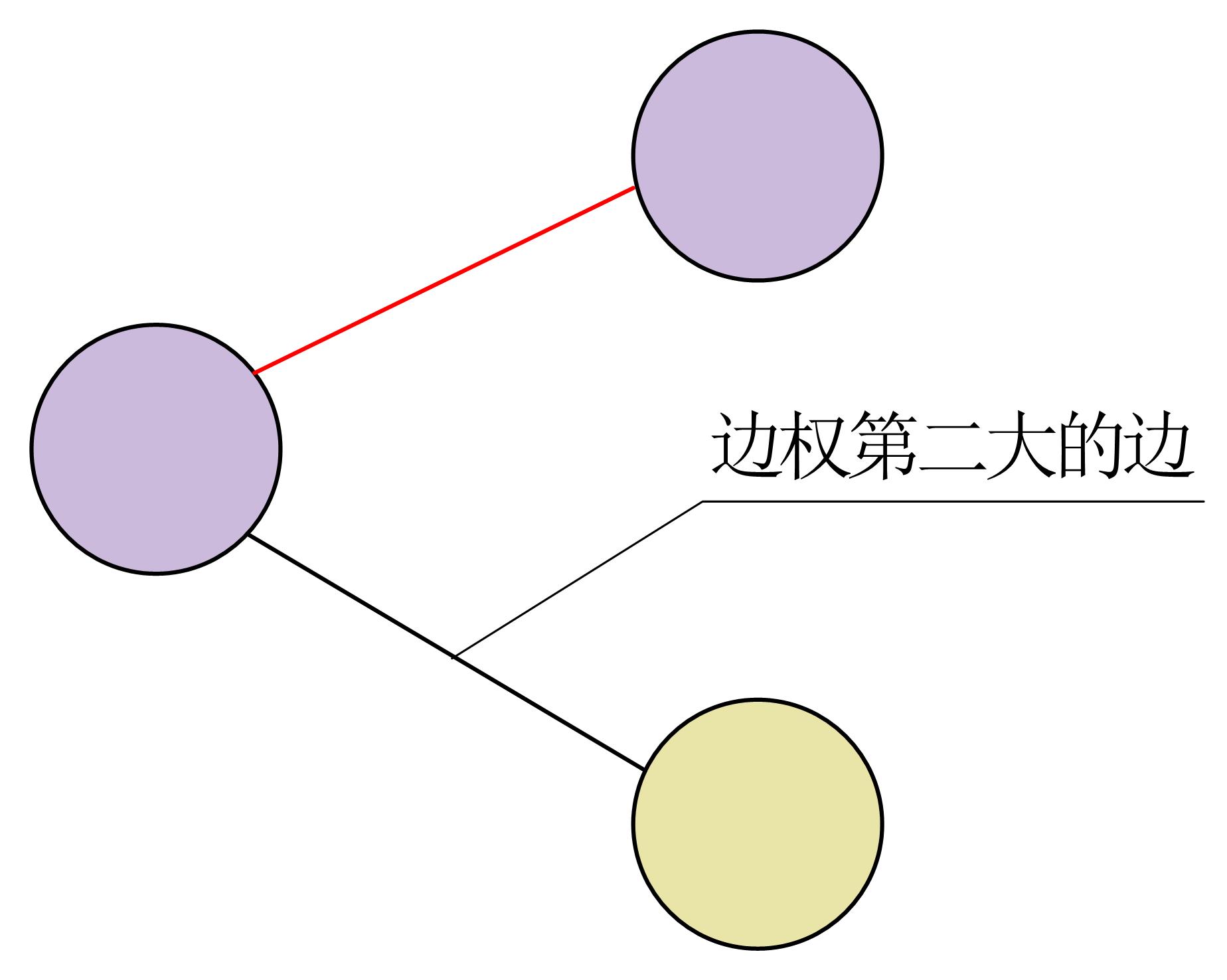
对于这种情况，可以直接把剩余的一个电话机放到黄色节点上，将边权最大的两个边全部删除。

情况二：

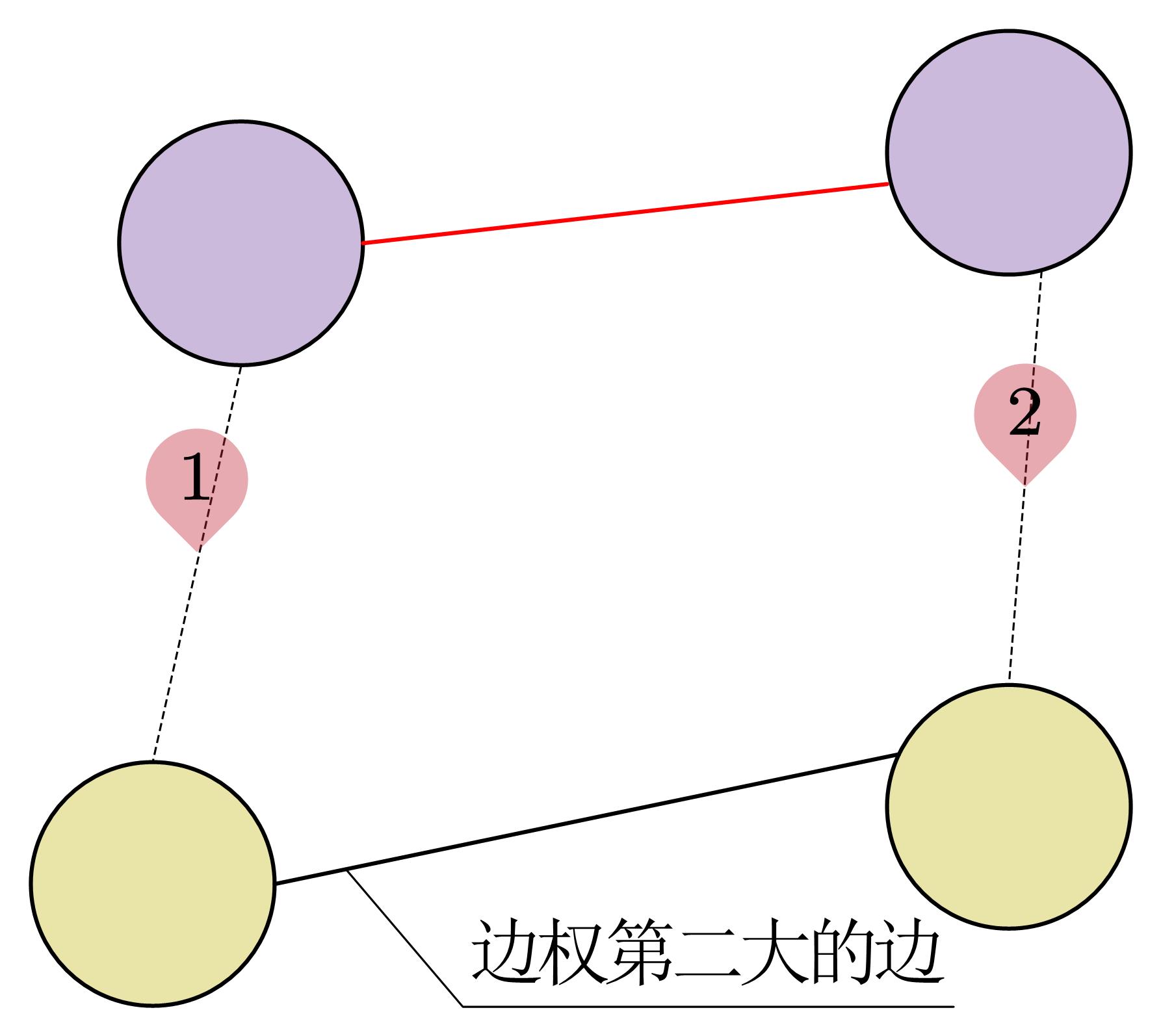
显然，编号为1和2的两个边不可能同时存在。当我们删去黄色结点之间的边时，红色边所连接的结点一定与两个黄色结点的其中之一属于同一个连通分量（假如都不属于则为森林， 假如都属于则为图）。因此，我们可以在不属于同一个连通分量的黄色结点上安装电话机，这样就可以删除第二大的边且保证MST连通不变。

所以经过分析，\(s\) 个电话机能删除 \(s-1\) 个边权最大的边。

代码如下：

代码

#include <bits/stdc++.h>
using namespace std;
#define DEBUG 0

#define all(x) x.begin(), x.end()
#define sz(x) (int(x.size()))
#define Case(x, y) ("Case #" + to_string(x) + ": " + to_string(y))
#define pb push_back
#define mp make_pair
#define fr(x) freopen(x, "r", stdin)
#define fw(x) freopen(x, "w", stdout)
using ll = long long;
using db = double;
using vi = vector<int>;
using vvi = vector<vi>;
using pii = pair<int, int>;

int s, p, tot;
const int maxn = 3e5 + 50;
struct edge{
    int u, v, w;
    bool operator<(const edge &other){
        return w < other.w;
    }
}edges[maxn];

struct DSU{
    vi parent;
    void init(int n){
        // 1-index
        parent.resize(n + 1);
        for (int i = 0; i <= n; ++ i) parent[i] = i;
    }
    int find(int x){
        return (x == parent[x]) ? x : parent[x] = find(parent[x]);
    }
    void to_union(int x, int y){
        int px = find(x), py = find(y);
        parent[py] = px;
    }
    bool is_same(int x, int y){
        return find(x) == find(y);
    }
}dsu;

using tup = tuple<int, int, int>;
void kruskal(){
    dsu.init(p + 1);
    vector<tup> eg; // 存最小生成树
    sort(edges, edges + tot);
    for (int i = 0; i < tot; ++ i){
        int u = edges[i].u, v = edges[i].v, w = edges[i].w;
        if (!dsu.is_same(u, v)){
            dsu.to_union(u, v);
            eg.push_back(make_tuple(u, v, w)); // 放入
        }
    }

    // s == 2 时显然能删去最大的
    // s == 3 时，假如边权第二大的生成树边(u2, v2)中的某一点为边权第一大的树边(u1, v1)中的一点直接可以删除，否则我们可以
    // 将其中一点eg: u2 与 (u1, v1) 相连，断开 u2, v2 这样 s 个电话可以断开 s - 1 个最大边
    int ans = get<2>(eg[p - s - 1]);
    cout << fixed << setprecision(2) << sqrt(1.0 * ans) << '\n';
}


void solve(){
    cin >> s >> p;
    tot = 0;
    vector<pii> arr;
    for (int i = 1; i <= p; ++ i){
        int x, y; cin >> x >> y;
        // 到每个结点的距离
        for (int k = 1; k <= sz(arr); ++ k){
            int cx = arr[k - 1].first, cy = arr[k - 1].second;
            edges[tot++] = {i, k, (cx - x) * (cx - x) + (cy - y) * (cy - y)}; // 为了方便距离没有开根号
        }
        arr.push_back({x, y});
    }
    kruskal();
}   


int main(){
    ios::sync_with_stdio(0), cin.tie(0);
    // fr("input.txt");
    int t = 1; // cin >> t;
    while (t--) solve();
    // fclose(stdin);
    return 0;
}