Codeforces Round #674 (Div. 3)
Codeforces Round #674 (Div. 3)
A. Floor Number
题目大意
题目大意为:一个学生公寓中有多个房间,每个房间有门牌号。已知一楼有且仅有两个房间,其门牌号分别为 1 和 2。给定数字 \(x\) ,之后每层楼中有 \(x\) 间房间。问:给你门牌号 \(n\) 和数字 \(x\) 。给出所在楼层。
1 <= n, x <= 1000
*800
解题思路
非常简单,分情况讨论:
- 如果 $n \leq 2 $ ,则返回 \(1\)
- 否则,\(n \leftarrow n - 2, ans = \lceil\dfrac{n}{x}\rceil\) 。
代码
void solve(){
int n = read(), x = read();
if (n <= 2) cout << 1 << '\n';
else cout << (n - 2 + x - 1) / x + 1 << '\n';
}
B. Symmetric Matrix
题目大意
用 \(n\) 个 \(2 \times 2\) 的正方形尝试拼接出一个 \(m\times m\) 的关于主对角线对称矩阵。
如果可以输出:
YES否则输出:NO
*900
解题思路
题目看起来有点麻烦,阅读起来也比较长,实际上仔细一想,只要边长能 mod 2,则我们运用贪心的思路考虑问题,只需要一个 \(2\times 2\) 的主对角线对称矩阵即可。
主要的思路方向是大小类比,转大为小。
代码
void solve(){
int n = read(), m = read();
int have = 0;
for (int i = 0; i < n; ++ i){
int ul = read(), ur = read();
int dl = read(), dr = read();
if (dl == ur) have = 1;
}
if (m % 2 != 0 || have == 0) wprint("NO");
else wprint("YES");
}
C. Increase and Copy
题目大意
给你一个数组 \(a\) ,最开始只包含一个数字 \(1\) 。你可以做如下两种操作:
- 给 \(a\) 中的某一元素加一
- 复制 \(a\) 中某一元素到数组末尾
回答,需要最少操作多少步,能使数组 \(a\) 中的总和大于 \(n\)。
1 <= n <= 1e9
*1100
思路分析
经过思考,显然倍增的效率是大于自增的,于是我们可以初步得出结论,我们需要先自增然后再倍增。
设我们自增到 \(k\) 再进行倍增。则需要的步骤数为:
处理一下变为:
由基本不等式可得:当 \(k = \sqrt{n}\) 时存在最小值,又因为这里皆为整数,通过计算机验证之后得到如下结论:
可以记住如上结论。
代码
void solve(){
int n = read();
int ans(0);
int x = sqrt(n);
ans = (n + x - 1) / x + x - 2;
cout << ans << '\n';
}
D. Non-zero Segments
题目大意
给定一个长度为 \(n\) 且不含 \(0\) 的序列 \(a\),可以插入任何数字(可以为 \(\infty\) )。请问最少插入多少个数字才能保证序列中任意连续子序列和不为 \(0\) 。
2 <= n <= 200000-1e9 <= ai <= 1e9
*1500
思路分析
这题关键点在于 快速确定区间和为 0 的情况。
因为做过类似的,所以可以很快的写出来:即用 hashmap。
接下来复制我在CF回复别人的部分:
Let us define \(presum_{k}\) as the prefix sum, \(a_k\) as the array.
Let's define \(i,j\) as indexs(\(i < j\)):
- if \(presum_{i} == presum_{j}\), we can know that
In order to avoid this situation, we insert a \(+\infty\) behind the \(a_j\). Like this: \(a_{i+1}, \cdots, a_{j-1}, \stackrel{\infty}{\downarrow},a_{j}\).Then reconsider from \(a_j\)

代码
void solve(){
int n = read();
unordered_map<LL, int> mp; // 0 --> not in, 1 --> in
mp.clear();
LL sum(0), ans(0);
for (int i = 0; i < n; ++ i){
int f = read();
sum += f;
if (sum == 0 || mp.count(sum)) {
++ ans;
mp.clear(); // Simulate inserting an infinite number
sum = f;
mp[sum] = 1;
}
else mp[sum] = 1;
}
cout << ans << '\n';
}
E. Rock, Paper, Scissors
题目大意
Alice和Bob进行剪刀石头布的游戏,总共进行\(n\)局。
Alice出石头\(a_1\)次,出剪刀\(a_2\)次,出布\(a_3\)次。
Bob出石头\(b_1\)次,出剪刀\(b_2\)次,出布\(b_3\)次。
问Alice最多赢多少次,最少赢多少次。
*1800
思路分析
最大值非常简单,我们希望尽可能能赢
实际上这题应该有更加数学的思路,但是考虑到整个问题空间的大小,因此可以通过暴力搜索直接解决。
面对样本空间很小的题目,我们可以优先计算穷举的复杂度,快速解决。
时间复杂度大致为 \(\mathcal{O}(2\cdot 3!)\)
代码
int a[5], b[5];
int mn;
void dfs(int ca, int cb, vector<int> visa, vector<int> visb, int cnt, vector<int> fa, vector<int> fb){
visa[ca] = visb[cb] = 1;
if (fa[ca] >= fb[cb]){
if ((ca + 1) % 3 == cb) cnt += fb[cb];
fa[ca] -= fb[cb];
int ok =0;
for (int i = 0; i < 3; ++ i){
if (visb[i] == 0) { // 谁没有了,就在他可选的中间挑选一个
dfs(ca, i, visa, visb, cnt, fa, fb);
ok = 1;
}
}
if (ok == 0){ // 没有什么可以选的了,说明结束了
mn = min(mn, cnt);
return;
}
}
else {
if ((ca + 1) % 3 == cb) cnt += fb[cb];
fb[cb] -= fa[ca];
int ok = 0;
for (int i = 0; i < 3; ++ i){
if (visa[i] == 0) {
dfs(i, cb, visa, visb, cnt, fa, fb);
ok = 1;
}
}
if (ok == 0){
mn = min(mn, cnt);
return;
}
}
}
void solve(){
int n = read();
for (int i = 0; i < 3; ++ i) a[i] = read();
for (int i = 0; i < 3; ++ i) b[i] = read();
int mx(0);
for (int i = 0; i < 3; ++ i) mx += min(a[i], b[(i + 1) % 3]);
VI visa(3, 0), visb(3,0); // visa --> a是否访问, visb --> b是否访问
VI fa(3, 0), fb(3, 0); // fa --> a 的各个数个数, fb --> 同 a
mn = inf;
for (int i = 0; i < 3; ++ i) fa[i] = a[i], fb[i] = b[i];
for (int i = 0; i < 3; ++ i){ // 枚举各种情况
for (int j = 0; j < 3; ++ j) dfs(i, j, visa, visb, 0, fa, fb);
}
wprint(mn, mx);
}
F. Number of Subsequences
题目大意
给定一个长为 \(n\) 含有
abc?的字符串,?可能是abc中的任意一个,求所有可能的无?字符串中,子序列abc出现的次数.结果需要 mod \(1e9 + 7\)
3 ≤ n ≤ 200000
*2000 dp
思路分析
通过数据大小和题目所问的,我们可以很快得出大致思路:时间复杂度为 \(\mathcal{O}(n)\) 的线性dp。
假如是 dp ,我们肯定需要记录一些东西才能保证在 \(\mathcal{O(1)}\) 的时间内进行状态转移,并且需要考虑记录什么和 ? 如何进行处理。
由于我们只需要考虑 abc ,因此我们可以只记录:
a的数量 \(f[0]\)ab的数量 \(f[1]\)abc的数量 \(f[2]\)
当没有遇到 ? 时转移方程非常简单,这里就不做赘述。
下面考虑当需要疑问号的情况即可:
首先,我们清楚疑问号可以变为 a,b,c 任意一种的,用生物学的知识去想有点像分裂的过程:
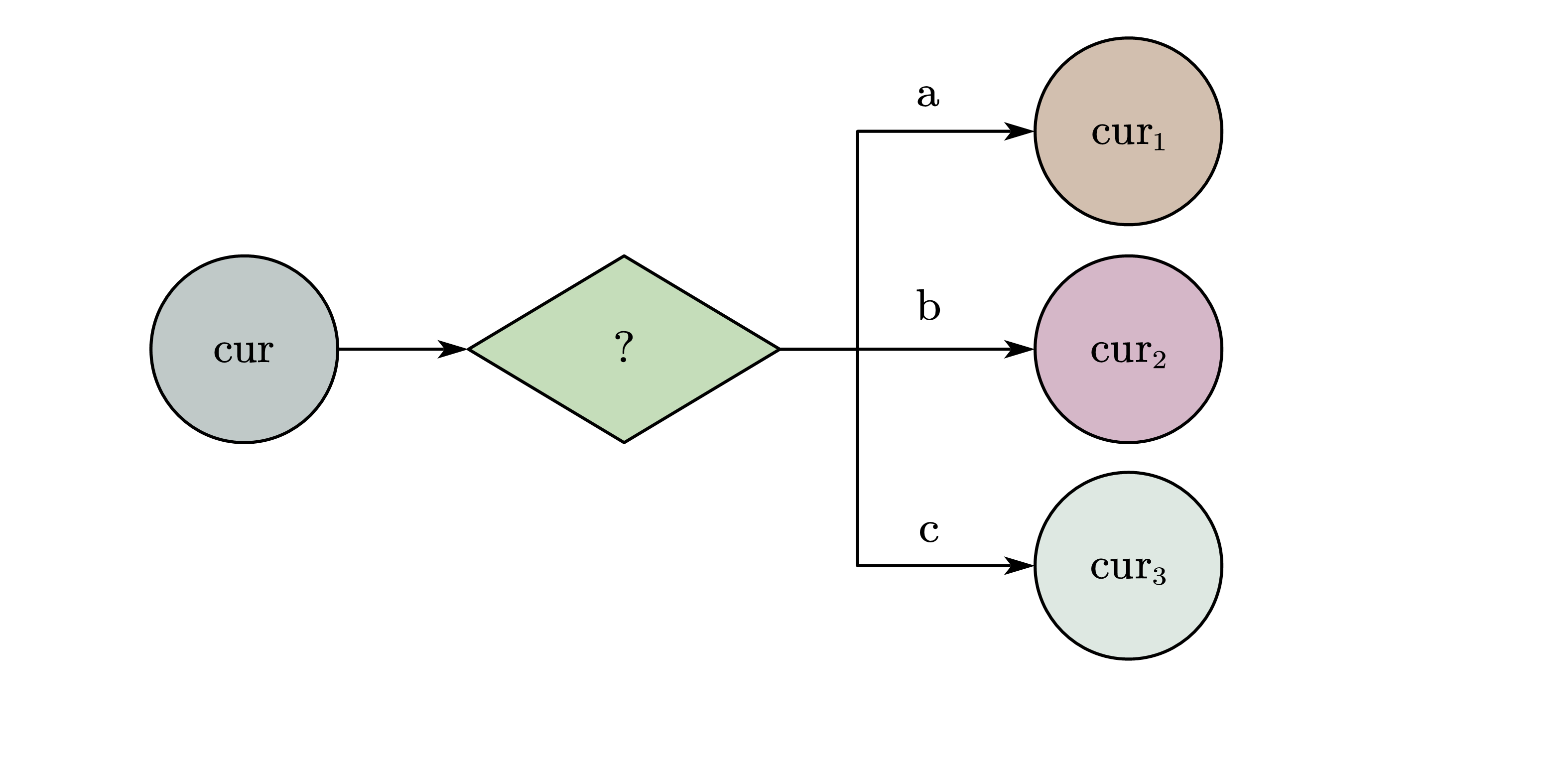
当碰到 ? 号时,会在原有的基础上出现 \(3\) 种新情况。
- 对于 \(cur_1\) 。其 \(f[0] = f[0] + 1\)
- 对于 \(cur_2\)。 其 \(f[1] = f[1] + f[0]\)
- 对于 \(cur_3\)。 其 \(f[2] = f[2] + f[1]\)
而他们各自又继承了 cur的所有值。因此:
这对了吗?,实际上这样写代表你没有理解其核心。需要知道的最开始只拥有 \(1\) 种情况,但每遇到一个 ? 会分裂出 \(3\) 种情况,不妨假设 ? 的个数为 \(c_q\) 。则当前存在 \(3^{c_q}\) 种情况,于是你每次增加都需要考虑所有的情况。而上述方程中:a -> ab 和 ab -> abc 的转移自带鲁棒性已经考虑了这个问题,而 null -> a 的过程则没有考虑。
因此,我们需要记录当前空间中存在情况的总个数 base ,当遇到 ? 时更新 base 的值。
做这种 \(\mathcal{O}(1)\) 的计数 dp ,肯定是需要记录某些数据,若需要计数的为一个具有顺序的序列,不妨前缀考虑每个子段的个数,逐个转移。
代码
const int maxn = 5;
LL f[maxn];
void solve(){
int n = read();
mst(f, 0);
string ss;
cin >> ss;
LL base = 1;
for (int i = 1; i <= n; ++ i){
char ch = ss[i - 1];
if (ch == 'a'){
f[0] = (f[0] + base) % MOD;
}else if (ch == 'b'){
f[1] = (f[1] + f[0]) % MOD;
}else if (ch == 'c'){
f[2] = (f[2] + f[1]) % MOD;
}else {
f[2] = (3 * f[2] % MOD + f[1]) % MOD;
f[1] = (3 * f[1] % MOD + f[0]) % MOD;
f[0] = (3 * f[0] % MOD + base) % MOD;
base = (1LL * base * 3) % MOD;
}
// print(f, 3);
}
cout << f[2] << '\n';
}
UPD:
小号变大号太真实了: