Codeforces Round #662 (Div. 2)
Codeforces Round #662 (Div. 2)
A. Rainbow Dash, Fluttershy and Chess Coloring
题目大意
给定一个 \(n \times n\) 的正方形区域,要求用两种颜色为其上色,且相邻的块颜色不能相同。每次上色能对任意块进行上色,但要求被上色的块的邻边是边界或是一个已经被上色的块。至少需要多少回合才能将正方形区域上色成功。
1 <= n <= 1e9
greedy math *800
思路分析
这题看 n 的数量级就猜测是一个规律题。
如何寻找规律呢?显然我们每次上色都是贪心的上尽可能多的块。
所以,我们第一次上色会将边界区域上色一半,第二次上色会完成边界区域的上色,并把已经上色的区域作为新的边界。

如图所示这是 n = 5 的情况下上色两次后的图例。在经过两次上色后,我们把已经上色的部分作为新的边界,因此我们从 n = 5 转移到了 n = 3。从图片上可以得到,两次操作后,我们从n = 5 转移为 n = 3 之后再进行了一次操作的结果。
由 n = 1 需要操作 1 次, n = 2 需要操作 2 次。且由 \(f(n) = f(n - 2) + 2 - 1 = f(n - 2) + 1\):
可以得到 :
代码
#include <bits/stdc++.h>
using namespace std;
#define LL long long
int main(){
int t; cin >> t;
while (t--){
int n; cin >> n;
cout << (n / 2) + 1 << '\n';
}
return 0;
}
B. Applejack and Storages
题目大意
给你一批木材,每个木材的长度用 \(a_i\) 表示,你需要用这批木材完成两个任务:
- 搭建一个正方形(需要 4 个一样长度的木材)
- 搭建一个矩形 (需要 2 组 2 个长度一样的木材,注意可以是 4 个一样长的)
每次会进行木材存储的合法更新,判断能否同时完成这两个任务。
1 <= ai <= 1e5
greedy implementation *1400
思路分析
这题很多人用传统的暴力算法,实际上这题想清楚思路非常简单。
注意,我们需要关注的只有:
- 当前 4 个一样长的木材的组数 \(four\)
- 除去 \(four\),之外 2 个一样长的木材的组数 \(two\)
为了便于理解举个例子:假如长为 1 的木材数量共有 7 个,则 \(four = 1, two = 1\)
那么能完成任务的条件就是:
- \(four \ge 2\)
- \(four == 1 \and two \ge 2\)
因此,我们目前只剩下如何得到 \(four, two\) 的值这个问题了。
下面通过 3 给例子完全阐明 \(four, two\) 值的处理,设长为 \(x\) 的木材共有 \(c\) 个,改变量为 \(dlt\) :
- 当 \(dlt = 1\)
- 此时 \(c = c + 1\), 若此时 \(c \% 4 == 0\),\(c\) 恰能整除 4 。这说明之前 \(c = 4 * k + 3\) ,其 \(four = k, two = 1\)。修改之后 $ c = 4 * (k + 1)$, \(four = k + 1, two = 0\)。 也就是
four += 1, two -= 1 - 若此时 \(c \% 4 != 0 \and c \% 2 == 0\),这说明之前 \(c = 4 * k + 1\),其\(four = k, two = 0\)。修改之后,$ c = 4*k + 2$, \(four = k, two = 1\)。只需要更新 \(two\),也就是
two += 1 - 若此时上述两种情况都不满足,则 \(c\) 原来一定是 \(c = 4*k \quad or \quad c = 4*k + 2\),这时候不需要对 \(four, two\) 进行修改。
- 此时 \(c = c + 1\), 若此时 \(c \% 4 == 0\),\(c\) 恰能整除 4 。这说明之前 \(c = 4 * k + 3\) ,其 \(four = k, two = 1\)。修改之后 $ c = 4 * (k + 1)$, \(four = k + 1, two = 0\)。 也就是
- 当 \(dlt = -1\) ,同样的道理
- 假如更新前 \(c = 8\),也就是恰好被 4 整除的情况。那么会减少一个 \(four\),增加一个 \(two\)。
- 假如更新前 \(c = 6\),也就是不被 4 整除,但被 2 整除的情况。那么只会减少一个 \(two\),不影响\(four\)
- 否则不需要更新 \(four, two\) 的值
因此算法流程就很清晰了:
- 预处理初始的木材,保存每个木材长度
ai的数量ci,并计算four,two - 更新木材数量和
four, two,判断是否满足条件。
代码
#include <bits/stdc++.h>
using namespace std;
const int maxn = 1e5 + 50;
int m[maxn]; // 记录每个木材长度有多少个
int main(){
int n; cin >> n;
memset(m, 0, sizeof(m));
int four = 0, two = 0;
for (int i = 0; i < n; ++ i){
int ci; cin >> ci;
++ m[ci];
if (m[ci] % 4 == 0) -- two, ++ four; // 情况一
else if (m[ci] % 2 == 0) ++ two; // 情况二
}
int q; cin >> q;
for (int i = 0; i < q; ++ i){
int dlt;
char sign;
cin >> sign >> dlt;
// cout << four << " " << two << endl;
if (sign == '+'){
++ m[dlt];
if (m[dlt] % 4 == 0) -- two, ++ four; // 情况一
else if (m[dlt] % 2 == 0) ++ two; // 情况二
if (four >= 2 || (four == 1 && two >= 2)) cout << "YES\n";
else cout << "NO\n";
}else {
int save = m[dlt];
-- m[dlt];
if (save % 4 == 0) -- four, ++ two;
else if (save % 2 == 0) -- two;
if (four >= 2 || (four == 1 && two >= 2)) cout << "YES\n";
else cout << "NO\n";
}
}
return 0;
}
C. Pinkie Pie Eats Patty-cakes
题目大意
给定 \(n\) 个数 \(a_i\),可以将所有数任意排列,求出相同的数之间的最小距离的最大值
1 <= n <=1e5
1 <= ai <= n
constructive algorithms greedy math sortings *1700
思路分析
这个题目,最开始想成模板二分题,绕了半天,后面发现之所以不能模板二分在于它不能简单的贪心放置,必须有策略的放。
那显然是一个贪心算法,关于贪心算法我做过总结,这个明显是一个离线贪心算法,也就是预处理完再利用设置好的贪心策略处理。
怎么才能让相同元素之间放更多元素呢?举个例子
首先我们有 4 个 1,我们这样放置1 1 1 1。
显然,我们需要在 1 之间的空隙进行补全,假设我们有 3 个 2: 1 2 1 2 1 2 1 这时候,距离为 2
再然后呢? 假设有 2 个 3:1 2 3 1 2 3 1 2 1,这时候距离还是为 2
也就是,我们必须在间隔中满满放置一轮,才能让答案增加 1,假如没放置满则不算。
你们可能会问我,假如 4 个 1 之后出现了 5 个 2 呢?
那就排序呀,保证从大到小就好了
那假如出现了 4 个 1 之后有 4 个 2 呢?
你会发现,效果与 3 个 2 一样
所以,贪心策略为:
- 我们首先预处理每个数字的数量,并对其按照数量从大到小排序
- 设最大数量
mxlen为基准,往其中mxlen - 1个间隔进行插入 - 若插满一轮,则答案加一
代码
#include <bits/stdc++.h>
using namespace std;
using LL = long long;
const int MOD = 1e9 + 7;
using pii = pair<int, int>;
const int maxn = 1e5 + 50;
int n, m[maxn];
vector<int> a;
struct node{
int name, cnt, pos; // 历史遗留,不需要考虑 pos
node(): name(-1), cnt(-1), pos(-1) {}
node(int _name, int _cnt): name(_name), cnt(_cnt), pos(-1) {}
};
void solve(){
cin >> n;
memset(m, 0, sizeof(m));
a.clear();
for (int i = 0; i < n; ++ i){
int ci; cin >> ci;
if (m[ci] == 0) a.push_back(ci); // 去重,将出现过的数字提取
++ m[ci];
}
vector<node> arr;
arr.clear();
for (int i = 0; i < a.size(); ++ i) arr.push_back({a[i], m[a[i]]});
sort(arr.begin(), arr.end(), [&](const node &a, const node &b){
return a.cnt > b.cnt;
});
int mxlen = -1, res = 0, count = 0;
for (int i = 0; i < arr.size(); ++ i){
if (mxlen == -1) { mxlen = arr[i].cnt; res = 0; continue; }
if (arr[i].cnt == mxlen) ++ res;
else {
count += arr[i].cnt;
res += (count / (mxlen - 1)); // 判断是否插满一轮
count = (count % (mxlen - 1)); // 插满之后剩余的
}
}
cout << res << endl;
}
int main(){
int t; cin >> t;
while (t--) solve();
return 0;
}
D. Rarity and New Dress
题目大意
给定一个 \(n \times m\) 的矩阵,矩阵由多个字母组成。找到矩阵中存在菱形的数量(其中单独一个也算做一个长度为 1 的菱形)
1 <= n, m <= 2000
dfs and similar dp implementation shortest paths *2100
思路分析
此题首先比较容易想到利用 动态规划 进行求解。但重点在于动态规划的 dp 数组的含义。
其思路来源于: 最大正方形,题目大意是在一个二进制矩阵中寻找一个最大的由 1 组成的正方形。
这题中 dp 数组的含义为 \(dp(i, j)\) 代表以位置 \((i, j)\) 作为正方形右下角的最大边长。为啥会选取右下角呢!搞清楚这个问题对于解决 当前菱形问题的解决有相当大的帮助。
一般来说,dp 多是顺序 dp ,当你遍历到位置 \((i, j)\) 时,往往只能从前面已处理完的位置获取信息。由此我们可以得到如下结论:在进行 dp 数组的设计时,需要保证转移方程只需要从已经处理完的位置获取信息。
例如,在本题中,假如 dp 数组设计为 dp[i][j] := 以 (i, j) 为中心的菱形最大长度 就会出现状态转移方程需要 \((i + 1, j)\) 的信息。而这个位置却是未处理过的。
因此,本题的 dp 数组含义的设计参考了上述结论, dp[i][j] := 以 (i, j) 作为低格的最大菱形长度
而状态转移方程呢:通过下图可以比较清晰的理解:
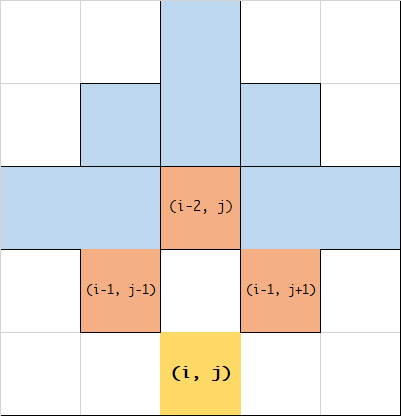
从图示可以发现,一个长为 3 的菱形,对于其底部 \((i, j)\) ,只需要判断 \((i - 1, j - 1), (i - 1, j + 1), (i - 2, j)\) 三个位置的最小值就能实现状态转移。(还需要判断 \((i - 1, j)\) 是否与 \((i, j)\) 为相同字母)
在得到这个结论后,我们便可以快速的写出代码了:
代码
#include <bits/stdc++.h>
using namespace std;
const int maxn = 2e3 + 50;
using LL = long long;
int dp[maxn][maxn];
int main(){
int n, m; cin >> n >> m;
vector<string> mat(2, string(m + 1, '$'));
for (int i = 0; i < n; ++ i){
string ss; cin >> ss;
mat.push_back("$" + ss);
}
// for (auto &e: mat) cout << e << '\n';
int ans = 0;
for (int i = 2; i <= n + 1; ++ i){
for (int j = 1; j <= m; ++ j){
if (mat[i][j] != mat[i - 1][j] || mat[i][j] != mat[i - 1][j - 1] || mat[i][j] != mat[i - 1][j + 1] || mat[i][j] != mat[i - 2][j])
dp[i][j] = 1;
else dp[i][j] = min({dp[i - 2][j], dp[i - 1][j - 1], dp[i - 1][j + 1]}) + 1;
ans += dp[i][j];
}
}
cout << ans << '\n';
return 0;
}
- 在以后进行类似这题的 几何dp 时,首先考虑以当前点作为几何图形的最下最右点,再设计 dp 方程。

