贪心算法总结
简介¶
贪心算法（英文：greedy algorithm），是用计算机来模拟一个“贪心”的人做出决策的过程。这个人十分贪婪，每一步行动总是按某种指标选取最优的操作。而且他目光短浅，总是只看眼前，并不考虑以后可能造成的影响。
可想而知，并不是所有的时候贪心法都能获得最优解，所以一般使用贪心法的时候，都要确保自己能证明其正确性。
本文主要介绍，在解决诸多贪心算法的问题之后的心得。
常用场景¶
最常见的贪心算法分为两种。
- 「我们将 XXX 按照某某顺序排序，然后按某种顺序（例如从小到大）选择。」。
- 「我们每次都取 XXX 中最大/小的东西，并更新 XXX。」（有时「XXX 中最大/小的东西」可以优化，比如用优先队列维护）
第一种是离线的，先处理后选择，第二种是在线的，边处理边选择。
常见的出题背景为:
- 确定某种最优组合（硬币问题）
- 区间问题（合理安排区间）
- 字典序问题
- 最值问题
\(\mathcal{A}\) 最优组合
硬币问题是贪心算法非常经典的题目，关于最优组合问题，我认为主要分为两种类型:
- 简单 -- 直接排序之后按照某种策略选取即可
- 复杂 -- 除了按照贪心策略外，还需要进行某些处理或者模拟
硬币问题
硬币问题 有1元、5元、10元、50元、100元、500元的硬币各\(C_1、C_5、C_{10}、C_{50}、C_{100}、C_{500}\)枚。现在要用这些硬币来支付\(A\)元，最少需要多少枚硬币？假设本题至少存在一种支付方法。
- \(0 \leq C_1、C_5、C_{10}、C_{50}、C_{100}、C_{500} \leq 10^9\)
- \(0 \leq A \leq 10^9\)
本题是上述说的简单类型的题目，简而言之要使得硬币最少，则优先使用大面额的硬币。
因此本题的解法便非常清晰了，只需要从后往前遍历一遍即可（默认为硬币已经按面额大小进行排序）
const int V[6] = {1, 5, 10, 50, 100, 500};
int A, C[6]; // input
void solve(){
int ans(0);
for (int i = 5; i >= 0; -- i){
int t = min(A / V[i], C[i]);
A -= t * V[i];
ans += t;
}
cout << ans << '\n';
}
零花钱问题
POJ3040 Allowance Description
As a reward for record milk production, Farmer John has decided to start paying Bessie the cow a small weekly allowance. FJ has a set of coins in \(N\) (1 <= N <= 20) different denominations, where each denomination of coin evenly divides the next-larger denomination (e.g., 1 cent coins, 5 cent coins, 10 cent coins, and 50 cent coins).Using the given set of coins, he would like to pay Bessie at least some given amount of money \(C\) (1 <= C <= 100,000,000) every week.Please help him ompute the maximum number of weeks he can pay Bessie.
Input
* Line 1: Two space-separated integers: \(N\) and \(C\)
* Lines 2..N+1: Each line corresponds to a denomination of coin and contains two integers: the value \(V\) (1 <= V <= 100,000,000) of the denomination, and the number of coins \(B\) (1 <= B <= 1,000,000) of this denomation in Farmer John's possession.
Output
* Line 1: A single integer that is the number of weeks Farmer John can pay Bessie at least C allowance
Sample Input
3 6 10 1 1 100 5 120Sample Output
111
这题的题目大意是:农场主每天都要给贝西至少为\(C\)的津贴。FJ有\(N\)数量的硬币，且每个硬币都能整除比他大的所有硬币。给定硬币的面额\(V_i\)及其数量\(B_i\)，求问这些钱最多能支付多少天的津贴。
这题和上一题比则更复杂些。因为存在几个难点:
- 策略从简单的取最大的变为支付更多天，需要进行“转义”
- 每找到一种方案，还需要考虑各个硬币数量的问题。
首先，我们明确知道，这个题目就是可以用贪心法去做。我们需要做的就是把目标具体化。需要支付更多天，实际上是要浪费更少的硬币。因此我们的方案应该是当前能浪费最少的方案。(大于目标值的硬币直接算作一天)
实际上，设临界值为\(V_{cur}\)，目标值为\(V_{tar}\),则存在 \(V_{cur} < V_{tar} , V_{cur} + V_i \ge V_{tar}\)。这时这个\(V_i\)必须是可选方案中最小的。
所以，我们可以：
- 先从大到小遍历一遍找到不超过\(V_{tar}\)的临界值。
- 再从小到大找到第一个可以使用的\(V_i\)。
- 统计该方案能实现的天数，更新答案和硬币数量。
int n, c;
vector<PLL> coins;
void solve(){
int res = 0;
for (int i = 0; i < n; ++ i){
LL val, num;
cin >> val >> num;
if (val >= c) res += num; // 大于直接加进去
else coins.push_back(MP(val, num));
}
sort(coins.begin(), coins.end()); // 排序
int sz = coins.size();
while (true){
LL tmp = c;
vector<int> use(sz, 0);
for (int i = sz - 1; i >= 0; -- i){ // 先大后小，在不超过cost的基础上不断逼近
use[i] = min(tmp / coins[i].first, coins[i].second); // 最多分配多少个
tmp -= coins[i].first * use[i]; // update
}
if (tmp){ // 假如没有恰好分配成功
for (int i = 0; i < sz; ++ i){ // 从小到大找到一个（为啥是一个？ 因为假如能加两个的话 之前就已经加上了，所以必定为一个
if (coins[i].second >= use[i] + 1){ // 要是直接 if (coins[i].second) 可能出现已经不够但还是支出的情况！
++ use[i];
tmp -= coins[i].first;
break;
}
}
}
if (tmp > 0) break;
LL mxu = 0x3f3f3f3f;
for (int i = 0; i < sz; ++ i) { // 找到最终该方案能分配多少个
if (use[i] == 0) continue;
mxu = min(mxu, coins[i].second / use[i]);
}
// cout << mxu << endl;
res += mxu;
for (int i = 0; i < sz; ++ i){ // update
coins[i].second -= (mxu * use[i]);
}
}
cout << res << '\n';
}
总结一下，这类最优组合类的贪心问题，大多是离线问题。需要我们首先找到贪心的主要策略，并通过一些小模拟进行处理相对来说，这类问题是比较简单的，只需要注意些模拟时容易出现的细节问题即可。
\(\mathcal{B}\) 区间问题
贪心算法在区间问题（如区间调度，区间安排，区间组合等）上的应用非常广泛。通常是需要对区间按照某种标准（如right endpoint)进行排序或者利用一些数据结构（如 priority_queue)进行
大致上我将贪心类的区间问题分为两类:
- 一维：工作时间、行程、建筑安排等
- 二维： 有关圆，半径等建筑安排等
下面通过分别介绍两个经典的例题进行分析：
一维区间
POJ3190 Stall Reservations Description
Oh those picky \(N\) (1 <= N <= 50,000) cows! They are so picky that each one will only be milked over some precise time interval \(A\cdots B\) (1 <= A <= B <= 1,000,000), which includes both times \(A\) and \(B\). Obviously, FJ must create a reservation system to determine which stall each cow can be assigned for her milking time. Of course, no cow will share such a private moment with other cows.
Help FJ by determining:
- The minimum number of stalls required in the barn so that each cow can have her private milking period
- An assignment of cows to these stalls over time
Many answers are correct for each test dataset; a program will grade your answer.
Input
Line 1: A single integer, \(N\)
Lines 2..N+1: Line i+1 describes cow i's milking interval with two space-separated integers.
Output
Line 1: The minimum number of stalls the barn must have.
Lines 2..N+1: Line i+1 describes the stall to which cow i will be assigned for her milking period.
Sample Input
5 1 10 2 4 3 6 5 8 4 7Sample Output
4 1 2 3 2 4Hint
Explanation of the sample:
Here's a graphical schedule for this output:
Time 1 2 3 4 5 6 7 8 9 10 Stall 1 c1>>>>>>>>>>>>>>>>>>>>>>>>>>> Stall 2 .. c2>>>>>> c4>>>>>>>>> .. .. Stall 3 .. .. c3>>>>>>>>> .. .. .. .. Stall 4 .. .. .. c5>>>>>>>>> .. .. ..Other outputs using the same number of stalls are possible.
题目的大意为：每头牛都有专属自己挤奶的时间间隔\([A, B]\)，且他们不愿意与别人在同一时间在 同一牛棚里挤奶，因此你要用尽可能少的牛棚保证这些奶牛能按时挤奶。
显然这是一个与区间安排有关的问题。这很像\(\mathcal{OS}\)中的串行并行问题，也就是每个CPU在一定时间内只能执行某个任务，请给出一个调度顺序使得使用的CPU个数最少。
首先我们需要考虑的问题为：最少需要多少个牛棚
其实很简单，我们只要知道同一时间段最多有多少头牛需要挤奶便可以知道最少需要多少个牛棚\(k\)。一方面假如牛棚数量小于\(k\)，则至少有一头牛无法安排。另一方面，不论区间具体如何，某一时间段最多有\(k\)头牛，需要同时挤奶则\(k\)个牛棚必定够用。
第二个问题是：如何安排牛棚呢？
实际上，思考一下进程的调度的实现便可以知晓答案。首先对于所有的区间按左端点从小到大进行排序，这样我们模拟了一个进程队列。我们依次将牛尝试添加到牛棚中，假如当前仍有空闲牛棚，则直接加入；否则找到一个已经用完的牛棚使用。（这里可以利用查分数组）
如何找到已经用完的牛棚呢？通过优先级队列便可以很简单的实现，每次分配一头牛时，将牛所属区间的右值（完成时间）压入到小根堆中，因此每次调度时判断堆顶的值是否小于当前区间的左值（最早的完成时间是否大于当前任务开始时间）。
所以这题的主要做法及思路如下：
- 思考如何进行贪心，优先安排开始时间早的牛，安排牛时判断是否有已经完成的牛
- 思考能否利用现有数据结构解决难点：优先级队列
- 进行解题
代码如下：
const int MAXM = 1e5 + 50;
const int MAXN = 1e6 + 50;
int n, diff[MAXN], res[MAXM]; // cow number / diff array / answer array
struct run
{
int flag; // 用了哪个牛棚
pair<PII, int> node; // {{start, end}, name}
run(): flag(-1), node({{-1, -1}, -1}){}
run(int _flag, pair<PII, int> _node): flag(_flag), node(_node) {}
};
bool cmp1(const pair<PII, int> &a, const pair<PII, int> &b){
return a.first < b.first;
}
bool operator< (const run &a, const run &b){
return a.node.first.second > b.node.first.second;
}
void solve(){
memset(diff, 0, sizeof(diff));
memset(res, 0, sizeof(res));
int l, r;
vector< pair<PII, int> > arr; // { {left, right}, name }
for (int i = 0; i < n; ++ i){
cin >> l >> r;
arr.push_back(MP(MP(l, r), i));
++ diff[l];
-- diff[r + 1];
}
// 找到牛棚数量
int k = 0, t = 0;
for (int i = 0; i < MAXN; ++ i){
t += diff[i];
k = max(k, t);
}
sort(arr.begin(), arr.end(), cmp1); // 确保left小的在左边
priority_queue<run, vector<run>> que; // 确保right小的在顶上
while (!que.empty()) que.pop(); // clear
int cnt = 1;
for (int i = 0; i < arr.size(); ++ i){
// que中没有node或者que中所有node在当前都未完成
if (que.empty() || que.top().node.first.second >= arr[i].first.first){
res[arr[i].second] = cnt;
que.push({cnt, arr[i]});
++ cnt;
}else {
run qt = que.top(); que.pop();
res[arr[i].second] = qt.flag;
que.push({qt.flag, arr[i]});
}
}
cout << k << endl;
for (int i = 0; i < n; ++ i){
cout << res[i] << endl;
}
}
实际上观察代码我们可以发现利用差分数组求解得到的\(k\)值，在后续求解中没有用到。实际上经过思考我们发现，可以去掉利用差分数组的求解最大牛棚的过程，可以直接利用贪心算法计算（也就是代码中的cnt)，这里之所以不去掉是因为包含了差分的思想，可能对后续有所帮助。
该题边处理，边更新是一个在线算法。
二维区间
POJ1328 Radar Installation Description
Assume the coasting is an infinite straight line. Land is in one side of coasting, sea in the other. Each small island is a point locating in the sea side. And any radar installation, locating on the coasting, can only cover \(d\) distance, so an island in the sea can be covered by a radius installation, if the distance between them is at most d.
We use Cartesian coordinate system, defining the coasting is the x-axis. The sea side is above x-axis, and the land side below. Given the position of each island in the sea, and given the distance of the coverage of the radar installation, your task is to write a program to find the minimal number of radar installations to cover all the islands. Note that the position of an island is represented by its x-y coordinates.
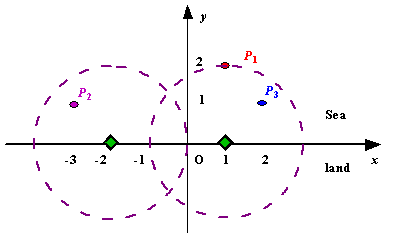
Figure A Sample Input of Radar Installations Input
The input consists of several test cases. The first line of each case contains two integers n (1<=n<=1000) and d, where n is the number of islands in the sea and d is the distance of coverage of the radar installation. This is followed by n lines each containing two integers representing the coordinate of the position of each island. Then a blank line follows to separate the cases.
The input is terminated by a line containing pair of zeros
Output
For each test case output one line consisting of the test case number followed by the minimal number of radar installations needed. "-1" installation means no solution for that case.
Sample Input
3 2 1 2 -3 1 2 1 1 2 0 2 0 0Sample Output
Case 1: 2 Case 2: 1
题目大意为：在陆地（x轴及其以下）上安装雷达，雷达的覆盖半径为\(d\)，要求用最少数量的雷达覆盖所有的岛屿。假如不能实现，则输出\(-1\)。
这题乍一看属于二维层面的（类似计算机集合）。但是他最后问的是最值问题，我们不难想到用贪心法尝试解决。实际上有多重贪心思路，并且很容易使用错误的贪心思路：
我们首先介绍一种错误的贪心思路并举出其反例：先对岛屿进行排序，从最左边开始，对每个岛屿求出能覆盖它且\(x\)值最大的雷达位置，跳过被该雷达覆盖的岛屿，从下一个未被覆盖的岛屿开始。
该想法犯了一个错误为：错把圆形当矩形，如何解释这句话？
设当前点为\(A - (x_a,y_a)\)，雷达位置为\((x_i,0)\)，满足\((x_i - x_a)^2 + y_a^2 = d^2\)。该想法认为雷达可摆放区间\([2x_a - x_i, xi]\)中，最右端一定能满足覆盖岛屿数量最多的条件。但由于覆盖范围是圆形，举极端条件：某个点\(B\)的位置为\((x_b, d)\)，则点必须在其正下方。
eg:
2 5
-5 3
-3 5
按照错误思路为: (-5, 3)可放雷达的最右端为-1，但是(-1, 0)无法覆盖(-3, 5)，因此答案为2
而实际上在(-3, 0)摆放雷达可同时覆盖两个，正确答案为1
可以说，上述思路忽视了二维区间的问题，将他简单的想象为一维区间贪心问题。
实际上，换一个思路问题便简单很多，我们寻找每个岛屿对应的雷达可安装范围（一个区间），转化为：存在多个一维区间，找到一种方案，使得每个区间上都存在一个点，且总点数最小。
解决这个一维区间问题便简单多了，通过排序贪心选取即可。（排序左右端点都可）
解题思路：
- 进行降维，找到每个岛屿的可安装雷达区间，转化为一维区间
- 对右端点排序，贪心选取右端点，重叠区间便跳过（排序左端点亦可，后续代码便排序了左端点）
struct Point{
int x, y;
Point(): x(0), y(0) {}
Point(int _x, int _y): x(_x), y(_y) {}
};
vector<PDD> segment;
// 降维为一维区间
PDD get_segment(Point island, int d){
db dlt = sqrt((d * d) - (island.y * island.y));
return MP(island.x - dlt, island.x + dlt);
}
// 区间贪心， 二维转一维
// 右端点为浮点数，注意类型一致问题！
int n, d;
void solve(){
int cnt = 1;
if (n == 0 && d == 0) break;
segment.clear();
int cx, cy, flag = 0;
for (int i = 0; i < n; ++ i){
cin >> cx >> cy;
if (cy > d || cy < 0) { flag = 1; continue; } // 输入没有结束，不要直接break
PDD seg = get_segment({cx, cy}, d);
segment.push_back(seg);
}
/* 存在不可到达island */
if (flag){
printf("Case %d: -1\n", cnt++);
continue;
}else{
// 对左端点排序
sort(segment.begin(), segment.end());
int res = 0;
db end; // 尾部断点为浮点数！
for (int i = 0; i < segment.size(); ++ i){
if (i == 0) { end = segment[i].second; ++ res; continue; }
if (segment[i].second < end){
end = segment[i].second; // 若区间右端点小于当前区间右端点，则更新
}else {
if (segment[i].first <= end) continue;
else {
end = segment[i].second;
++ res;
}
}
}
printf("Case %d: %d\n", cnt++, res);
}
}
总结：
面对一维区间，首先尝试排序左右端点，或者区间长度，设计合理的贪心策略进行求解，切忌盲目自信
面对二维区间等多维区间，可以先尝试进行降维，转化到熟悉的一维区间进行处理。
\(\mathcal{C}\) 易错杂项
POJ3262 Protecting the Flowers Description
Farmer John went to cut some wood and left \(N\) (2 ≤ \(N\) ≤ 100,000) cows eating the grass, as usual. When he returned, he found to his horror that the cluster of cows was in his garden eating his beautiful flowers. Wanting to minimize the subsequent damage, FJ decided to take immediate action and transport each cow back to its own barn.
Each cow i is at a location that is \(T_i\) minutes (1 ≤ \(T_i\) ≤ 2,000,000) away from its own barn. Furthermore, while waiting for transport, she destroys \(D_i\) (1 ≤ \(D_i\) 100) flowers per minute. No matter how hard he tries, FJ can only transport one cow at a time back to her barn. Moving cow i to its barn requires \(2 × T_i\) minutes (\(Ti\) to get there and \(T_i\) to return). FJ starts at the flower patch, transports the cow to its barn, and then walks back to the flowers, taking no extra time to get to the next cow that needs transport.
Write a program to determine the order in which FJ should pick up the cows so that the total number of flowers destroyed is minimized.
Input
Line 1: A single integer N
Lines 2..N+1: Each line contains two space-separated integers, Ti and Di, that describe a single cow's characteristicsOutput
Line 1: A single integer that is the minimum number of destroyed flowers
Sample Input
6 3 1 2 5 2 3 3 2 4 1 1 6Sample Output
86Hint
FJ returns the cows in the following order: 6, 2, 3, 4, 1, 5. While he is transporting cow 6 to the barn, the others destroy 24 flowers; next he will take cow 2, losing 28 more of his beautiful flora. For the cows 3, 4, 1 he loses 16, 12, and 6 flowers respectively. When he picks cow 5 there are no more cows damaging the flowers, so the loss for that cow is zero. The total flowers lost this way is 24 + 28 + 16 + 12 + 6 = 86.
本题大意是牛距离家\(T_i\)分钟的路程且其每分钟能吃\(D_i\)朵花，每牵一头牛需要\(T_i\)的时间（来回），则如何安排能使得损失最小。
本题有两个关键量，\(T_i\)，\(D_i\)。面对这种问题有多个参数且看起来是贪心法的问题，我们通过比较两个个体之间的优劣进行排序，再进行选择。
考虑有两头牛\(A,B\)，每头牛都有两个属性即：\(t(time),d(damgae)\)。假如选牛\(A\)，则损失为：\(2 * B.d * A.t\)，假如选择牛\(B\)，则损失为\(2*A.d * B.t\)，我们要求损失最小，因此比较\(\frac{A.t}{A.d}\)的大小即可，越小的说明该方案越优（姑且称为效率）
所以我们自定义比较函数，排序后选择最小的即可。
#define LL long long
const int maxn = 1e6 + 50;
struct cow{
LL t, d;
// bool operator< (const cow &b){
// return this->t * b.d < this->d * b.t;
// } C++ 11才允许
}C[maxn];
int sum[maxn];
bool cmp(const cow &a, const cow &b){
return a.t * b.d <= a.d * b.t;
}
int n; // input
void solve(){
memset(sum, 0, sizeof(sum));
for (int i = 0; i < n; ++ i){
scanf("%lld %lld", &C[i].t, &C[i].d);
}
sort(C, C + n, cmp);
for (int i = 0; i < n; ++ i){
if (i == 0) sum[i] = C[i].d;
else sum[i] = sum[i - 1] + C[i].d;
}
LL res = 0;
for (int i = 0; i < n; ++ i){
res += (2 * C[i].t * (sum[n - 1] - sum[i]));
}
printf("%lld\n", res); // res 是LL啊！
}
总结：面对多参数问题，通过比较两个个体的优劣缺点排序优先级，进而
