最小生成树系列问题
最小生成树
给定一张边带权的无向图\(G=(V,E)\),点数为\(n\),边数为\(m\),从\(E\)中选择\(n-1\)条使\(n\)个点全部联通的边组成的一颗树被称为该图的生成树,这一张图中权值最小的生成树叫做最小生成树(MST)。
定理
任何一颗最小生成树一定包含图上边权最短的一条边。
证明:假设最小生成树上不包含图\(G\)中权值最小的一条边\(e\),那么加入边\(e\)会形成一个环,此时一定可以找到另外一条边,删去后形成一颗生成树,此时新树的权值小于旧树。
推论:假设图中有一些点已经联通了,形成了一个联通森林,此时需要在连上一条边形成一颗权值最小的生成树,此生成树一定包括当前权值最小的连接两个不连通节点的边。
基于以上推论,我们有以下两种最小生成树算法。
Kruskal算法
Kruskal是一个贪心算法,它每一次寻找图中边权最小的连接未联通的两个点的一条边,将其加入到生成森林中,其中节点联通情况可以用并查集维护(并查集)。
算法流程:
1.并查集初始化。
2.将所有的边按照边权排序。
3.按边权从小到大扫每一条边,当发现这一条边连接的是两条不连通的边则把这条边加入生成森林中,并且用并查集合并这条边两端节点所在集合,若两点已经联通则忽略。
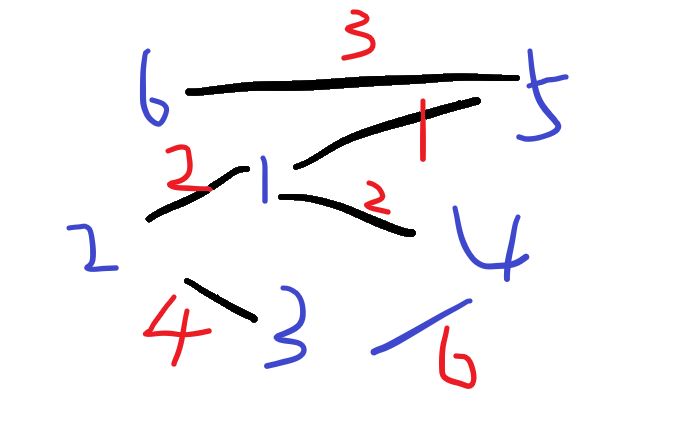
可以看一下下面的图:
这是原图

我们先找到边1-5,发现1和5不在同一个集合内,将这两个集合合并。
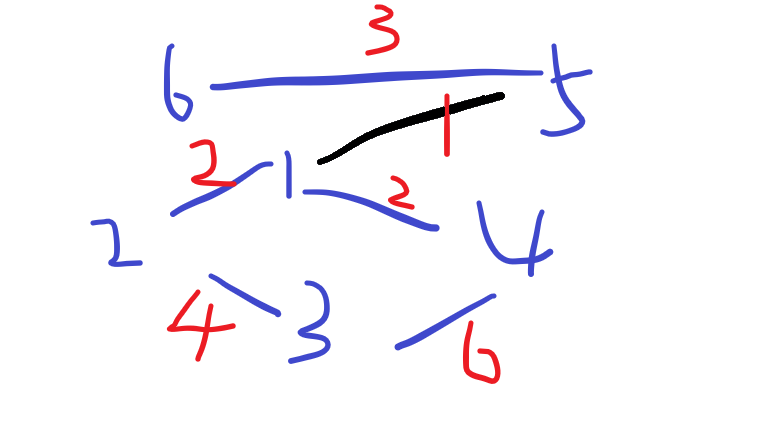
找到边1-2,不在同一个集合内,将两个集合合并
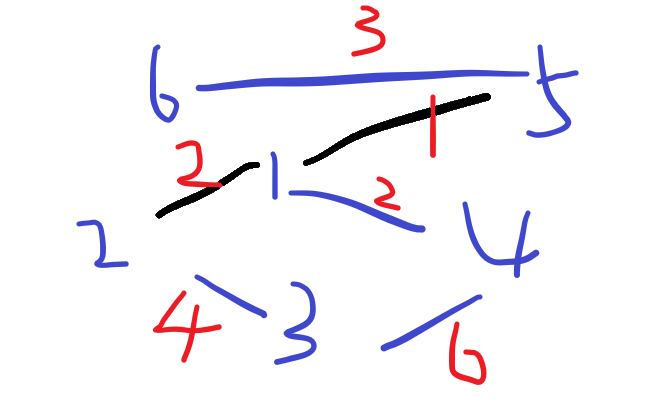
找到边1-4,不在同一个集合内,将两个集合合并
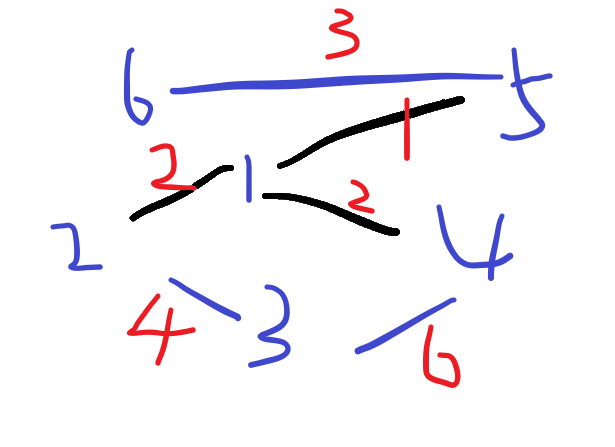
找到边5-6,不在同一个集合内,将两个集合合并
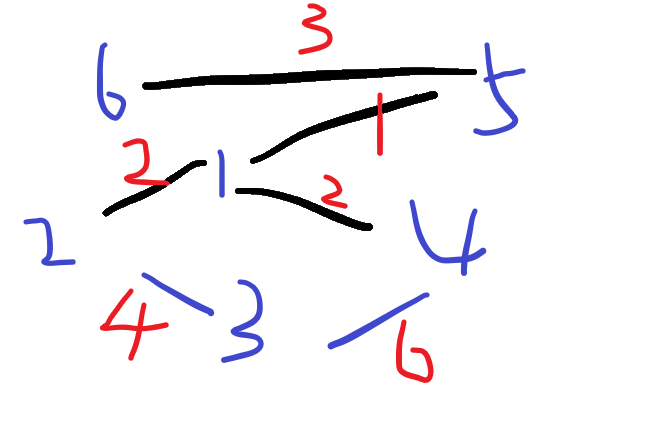
找到边3-2,不在同一个集合内,将两个集合合并
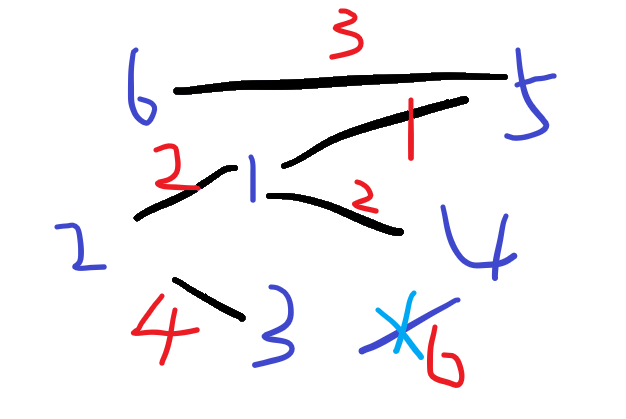
找到边3-4,在同一个集合内,不将两个集合合并
复杂度分析:Kurskal算法的瓶颈就在于排序,时间复杂度为\(O(m \log m)\)
Code:
#include<bits/stdc++.h>
using namespace std;
struct bian
{
int a,b,c;
}ss[600000];
int cmp(bian ss1,bian ss2)
{
return ss1.c<ss2.c;
}
int n,m,ans=0,f[600000];
int find(int x)
{
if(x==f[x])return x;
else return f[x]=find(f[x]);
}
int merge(int x,int y){f[find(x)]=find(y);}
int main()
{
scanf("%d%d",&n,&m);
for(int i=1;i<=m;i++)scanf("%d%d%d",&ss[i].a,&ss[i].b,&ss[i].c);
sort(ss+1,ss+m+1,cmp);
for(int i=1;i<=n;i++)f[i]=i;
for(int i=1;i<=m;i++)
{
int o=find(ss[i].a),p=find(ss[i].b),q=ss[i].c;
if(o!=p)
{
ans+=q;
merge(ss[i].a,ss[i].b);
}
}
printf("%d\n",ans);
return 0;
}
prim算法
prim算法也是基于上述推论的,做法与Kruskal不同,这个算法将图上的点分成两个集合\(S\)和\(T\),\(S\)集合表示已经加入到生成树中的点的集合,\(T\)集合表示暂时还没有加入到是生成树中的点的集合。
假设图\(G=<V,E>\)。
一开始,\(S\)集合仅包含源点\(s\),\(T\)集合包含除了源点以外的\(n-1\)个点。
每一次我们找出一条最小的边\(e\)满足e联通的是\(S\)集合中的点和\(T\)集合中的点。
我们需要一个数组\(d\),表示所有节点距离\(S\)集合的最短距离,其中规定\(\forall x \in S,d[x]=0\)。
算法流程:
1.将d数组初始化为\(\infty\)。
2.将源点\(s\)标记(说明已经在\(S\)集合),并将其他点用它和源点的距离更新(不存在连边的两个点之间距离为\(\infty\))。
3.每次找出一个还未被打上标记的距离和\(S\)集合最近的节点\(x\)。
4.将\(ans+=d[x]\),并将x打上标记。
5.用\(x\)来更新其他节点的\(d\)值。
复杂度分析:我们一共会找到\(n\)个点,每次查找和更新都会找到\(n\)个点,因此prim算法的时间复杂度为\(O(n^2)\)。
优化:其实我们可以用堆优化prim算法,时间复杂度为\(O(m \log n)\),但是堆优化的prim算法还不如直接使用kruskal算法,prim算法适合在稠密图尤其是完全图进行最小生成树的求解。
Code:
#include<bits/stdc++.h>
#define maxn 5100
using namespace std;
int n,m,x,y,z;
int w[maxn][maxn],d[maxn],ans=0;
bool vis[maxn];
void prim()
{
vis[1]=1;
for(int i=1;i<=n;i++)
d[i]=w[1][i];
for(int i=1;i<n;i++)
{
int maxp=1e9,maxq=1e9;
for(int j=1;j<=n;j++)
if(!vis[j]&&d[j]<maxp)
maxp=d[j],maxq=j;
vis[maxq]=1;d[maxq]=0;ans+=maxp;
for(int j=1;j<=n;j++)
if(!vis[j])
d[j]=min(d[j],w[maxq][j]);
}
}
int main()
{
scanf("%d%d",&n,&m);
memset(w,31,sizeof(w));
for(int i=1;i<=m;i++)
{
scanf("%d%d%d",&x,&y,&z);
int d=min(z,w[x][y]);
w[x][y]=d;w[y][x]=d;
}
for(int i=1;i<=n;i++)w[i][i]=0;
prim();
printf("%d\n",ans);
return 0;
}
以下为最小生成树的扩展问题:
次小生成树
次小生成树分为严格次小生成树和非严格次小生成树两种,我们首先来求解严格次小生成树问题。
首先我们有这样一个定理:
次小生成树一定是在最小生成树的基础上修改一条边。
这个定理其实很容易证明,我们如果修改了两条边,一定不会比可以修改一条边优秀。
然后我们就有了一个基本的思路:修改可以看作添加一条边并删除另外的一条边,我们可以先枚举一条没有在最小生成树上的边\(e\),将\(e\)加入最小生成树后肯定会形成一个环,此时我们只要删去环上的一条边(除去刚刚添加上的一条边),就可以形成一颗新的生成树,这棵生成树的边权之和一定大于等于最小生成树的边权和。
那么我们删去拿一条边呢?
根据贪心算法,我们肯定要删除一条边权最大的边,我们可以用倍增求出新加的一条边两个端点的lca,然后统计一下在原来的最小生成树上这两个节点之间最大边权,统计一下答案即可。
算法流程:
1.用kruskal算法求出最小生成树的边权和,并且标记一下在最小生成树上的边。
2.枚举每一条不在最小生成树上的边\(e\),它连接了节点\(a\)和\(b\)。
3.跑倍增算法(前置知识),求出\(a\)和\(b\)的lca,并且求出这两个节点的路径上的边权最大值。
4.统计答案。\(ans\)为最小生成树边权之和,\(sum\)为次小生成树边权之和,\(val\)为\(e\)的权值,\(val_0\)为倍增算法求出的边权最大值,我们写成\(sum=min(sum,ans+val-val0)\)即可。
这样我们就解决了非严格次小生成树问题。
但是我们注意到这题要求的是严格次小生成树,也就是我们次小生成树的权值之和必须小于最小生成树的权值之和。
我们有些时候倍增求出来的最大值\(val0=val\),此时我们就不能使用最大值了,而需要使用次大值\(val'\),仍然使用倍增维护,但是很麻烦(有些大佬可以用高级数据结构维护,例如LCT)。
当我们发现\(val0=val\)时,我们使用次大值更新答案\(sum=min(sum,ans+val-val')\)。
Code:
#include<bits/stdc++.h>
#define int long long
#define maxn 300010
using namespace std;
int n,m,ans=0,f[maxn/2][20],w[maxn/2][20],sum=1e15,fa[maxn],c[maxn/2][20];
int cnt=0,pre[maxn*2],now[maxn*2],son[maxn*2],val[maxn*2];
int dep[maxn];
int cdz=0;
int cp[8];
struct bian
{
int x,y,v;
bool ok;
bool operator < (const bian &xx1)const
{
return v<xx1.v;
}
}q[maxn];
int put(int x,int y,int z)
{
pre[++cnt]=now[x];
now[x]=cnt;
son[cnt]=y;
val[cnt]=z;
}
int find(int x)
{
if(x==fa[x])return x;
else return fa[x]=find(fa[x]);
}
int mst()//kruskal板子
{
ans=0;
sort(q+1,q+m+1);
for(int i=1;i<=n;i++)fa[i]=i;
for(int i=1;i<=m;i++)
{
q[i].ok=0;
int fx=find(q[i].x),fy=find(q[i].y);
if(fx==fy)continue;
q[i].ok=1;
ans+=q[i].v;
fa[fx]=fy;
}
}
int dfs(int x,int ff,int vv,int dd)
{
f[x][0]=ff,w[x][0]=vv,c[x][0]=0;
for(int i=1;i<=17;i++)
{
cp[1]=w[x][i-1],cp[2]=w[f[x][i-1]][i-1],cp[3]=c[x][i-1],cp[4]=c[f[x][i-1]][i-1];//倍增维护次大值,最大值,lca
f[x][i]=f[f[x][i-1]][i-1],w[x][i]=max(w[x][i-1],w[f[x][i-1]][i-1]);
sort(cp+1,cp+5);//把所有可能的次大值排序,然后查找次大值(不一定是cp[3],因为有可能cp[3]=cp[4],我们规定次大值小于最大值)
/*
f[x][i]表示x节点的2^i辈祖宗
w[x][i]表示x节点到f[x][i]路径上的最大边权
c[x][i]表示x节点到f[x][i]路径上的次大边权(c[x][0]=0)
*/
int t=4;
c[x][i]=cp[4];
while(c[x][i]==w[x][i])c[x][i]=cp[--t];
}
dep[x]=dd;
for(int p=now[x];p;p=pre[p])
{
int t=son[p];
if(t==ff)continue;
dfs(t,x,val[p],dd+1);
}
}
int lca(int x,int y)//倍增求lca,顺便求出最大值和次大值
{
if(dep[x]<dep[y])swap(x,y);
int maxx=0;
cdz=0;
for(int i=17;i>=0;i--)
if(dep[f[x][i]]>=dep[y])
{
cp[1]=maxx,cp[2]=w[x][i],cp[3]=cdz,cp[4]=c[x][i];
maxx=max(maxx,w[x][i]),x=f[x][i];
sort(cp+1,cp+5);//排序,方法同上
int t=4;
cdz=cp[4];
while(cdz==maxx)cdz=cp[--t];
}
for(int i=17;i>=0;i--)
if(f[x][i]!=f[y][i])
{
cp[1]=cdz,cp[2]=maxx,cp[3]=c[x][i],cp[4]=c[y][i],cp[5]=w[x][i],cp[6]=w[y][i];
sort(cp+1,cp+7); //方法同上
maxx=max(maxx,max(w[x][i],w[y][i])),x=f[x][i],y=f[y][i];
int t=6;
cdz=cp[6];
while(cdz==maxx)cdz=cp[--t];
}
maxx=max(maxx,max(w[x][0],w[y][0]));//注意这里还有两条边需要更新
cp[1]=cdz,cp[2]=w[x][0],cp[3]=w[y][0];
int t=3;
sort(cp+1,cp+4);
cdz=cp[3];
while(cdz==maxx)cdz=cp[--t];
return maxx;
}
signed main()
{
scanf("%lld%lld",&n,&m);
for(int i=1;i<=m;i++)
scanf("%lld%lld%lld",&q[i].x,&q[i].y,&q[i].v);
mst();
for(int i=1;i<=m;i++)
if(q[i].ok)
put(q[i].x,q[i].y,q[i].v),put(q[i].y,q[i].x,q[i].v);
dfs(1,0,0,1);
for(int i=1;i<=m;i++)//枚举每一条边
{
if(!q[i].ok)
{
int p=lca(q[i].x,q[i].y);
if(q[i].v<=p)p=cdz;//最大值等于边权时,用次大值更新
sum=min(sum,ans+q[i].v-p);
}
}
printf("%lld\n",sum);
return 0;
}
其实这一题也可以用树链剖分和LCT维护。
最小度限制生成树
这一题我们需要用到wqs二分(带权二分)。
wqs二分是一个神奇的东西,经常用来把限制条件转化为二分来降低时间复杂度。
我们这一题有一个新的限制条件:一个节点\(s\)的度数为\(k\)(就是\(s\)连了\(k\)条边)。
我们先跑一遍最小生成树,求出边权和\(ans\)和\(s\)的度数\(num\)。
当\(num=k\)时,直接输出答案。
当\(num>k\)时:
我们二分一个\(mid\),将与节点\(s\)连接的所有边的边权加上\(mid\),再跑最小生成树,这样\(num\)就会变小,当\(num<k\)时\(r=mid-1\),\(num>k\)时\(l=mid+1\),当发现\(num==k\)时输出答案\(ans-mid*k\)。
当\(num<k\)时:
我们二分一个\(mid\),将与节点\(s\)连接的所有边的边权减去\(mid\),再跑最小生成树,这样\(num\)就会变大,当\(num<k\)时\(l=mid+1\),\(num>k\)时\(r=mid-1\),当发现\(num==k\)时输出答案\(ans+mid*k\)。
Code:
#include<bits/stdc++.h>
#define maxn 510000
using namespace std;
struct bian
{
int x,y,v;
bool operator < (const bian &xx1)const
{
return v<xx1.v;
}
}q[maxn];
int n,m,s,k,tmp=0,f[maxn],ans=0,ans0=0;
inline int read()
{
int x=0,y=1;char c=getchar();
while (c<'0'||c>'9') {if (c=='-') y=-1;c=getchar();}
while (c>='0'&&c<='9') x=x*10+c-'0',c=getchar();
return x*y;
}
int find(int x)
{
if(x==f[x])return x;
else return f[x]=find(f[x]);
}
int mst()//kruskal算法模板
{
ans=0,ans0=0;
sort(q+1,q+m+1);
for(int i=1;i<=n;i++)f[i]=i;
for(int i=1;i<=m;i++)
{
int fx=find(q[i].x),fy=find(q[i].y);
if(fx==fy)continue;
if(q[i].x==s||q[i].y==s)ans0++;
ans+=q[i].v;
f[fx]=fy;
}
}
int main()
{
n=read(),m=read(),s=read(),k=read();
for(int i=1;i<=m;i++)
q[i].x=read(),q[i].y=read(),q[i].v=read();
mst();
if(ans0==k)
printf("%d\n",ans);
else if(ans0>k)
{
int l=1,r=4e4;
while(l<=r)
{
int mid=(l+r)/2;
for(int i=1;i<=m;i++)
if(q[i].x==s||q[i].y==s)
q[i].v+=mid;
mst();
if(ans0>k)l=mid+1;
if(ans0==k)
{
printf("%d\n",ans-mid*k);
return 0;
}
if(ans0<k)r=mid-1;
for(int i=1;i<=m;i++)
if(q[i].x==s||q[i].y==s)
q[i].v-=mid;
}
printf("Impossible\n");
return 0;
}
if(ans0<k)
{
int l=1,r=4e4;
while(l<=r)
{
int mid=(l+r)/2;
for(int i=1;i<=m;i++)
if(q[i].x==s||q[i].y==s)
q[i].v-=mid;
mst();
if(ans0>k)r=mid-1;
if(ans0==k)
{
printf("%d\n",ans+mid*k);
return 0;
}
if(ans0<k)l=mid+1;
for(int i=1;i<=m;i++)
if(q[i].x==s||q[i].y==s)
q[i].v+=mid;
}
printf("Impossible\n");
return 0;
}
return 0;
}
最优比例生成树
这是一个0/1分数规划问题,0/1分数规划的经典解法是实数域的二分。
我们二分一个比值mid,然后就有这样一个式子。
\(\frac {\sum a[i]*x[i]} {\sum b[i]*x[i]}=mid\)
\(\sum a[i]*x[i]=mid* \sum b[i]*x[i]\)
\(\sum a[i]*x[i] -mid* \sum b[i]*x[i]=0\)
\(\sum x[i]*(a[i]-mid*b[i])=0\)
然后,我们就要考虑\(mid\)这个答案是否存在。
我们可以将\(a[i]-mid*b[i]\)作为每一条边的边权,跑一边最小生成树,就求出了\(Min_{x[i]*(a[i]-mid*b[i])}\)
若\(Min<0\),则说明\(Min(\frac {\sum a[i]*x[i]} {\sum b[i]*x[i]}) < mid\)
说明我们当前的\(mid\)还比答案要大,应当\(r=mid\)(实数二分不能写成\(r=mid-1\)),此时我们可以用\(mid\)来更新一下答案(此时的\(mid\)值是可以达到的)。
在此处更新答案是防止在一定的精度限制下找不到\(Min=0\)的情况。
若\(Min>0\),则说明\(Min(\frac {\sum a[i]*x[i]} {\sum b[i]*x[i]}) > mid\)
说明我们当前的\(mid\)比答案最小值还要小,应当\(l=mid\),此时的\(mid\)值无法达到,我们不能用它来更新答案。
若\(Min=0\),则说明\(Min(\frac {\sum a[i]*x[i]} {\sum b[i]*x[i]}) = mid\)
直接输出\(mid\)即可。
注意实数域上的二分要有精度限制
注意:这一题要用prim算法,kruskal算法会被卡(完全图)。
Code:
#include<bits/stdc++.h>
#define int long long
using namespace std;
int n;
long double L,xx[10050],yy[10050],zz[10050],ans=1e9;
long double a[1002][1002],b[1002][1002],d[10050];
bool vis[10050];
struct q
{
int x,y,h,l,v;
}q[1005000];
int prim(long double now)//Prim模板
{
L=now;
memset(vis,0,sizeof(vis));
for(int i=1;i<=n;i++)
d[i]=a[1][i]-L*b[1][i];
vis[1]=1;
long double sum=0;
for(int i=1;i<n;i++)
{
long double maxp=1e9;
int maxq=1e9;
for(int j=1;j<=n;j++)
if(!vis[j]&&d[j]<maxp)
maxp=d[j],maxq=j;
sum+=maxp,vis[maxq]=1,d[maxq]=0;
for(int j=1;j<=n;j++)
if(!vis[j]&&d[j]>a[maxq][j]-L*b[maxq][j])
d[j]=a[maxq][j]-L*b[maxq][j];
}
if(sum>0)return 1;
if(sum==0)return 0;
if(sum<0)return -1;
}
signed main()
{
while(true)
{
ans=1e9;
scanf("%lld",&n);
if(n==0)return 0;
for(int i=1;i<=n;i++)
scanf("%Lf%Lf%Lf",&xx[i],&yy[i],&zz[i]);
for(int i=1;i<=n;i++)
{
for(int j=i+1;j<=n;j++)
{
b[i][j]=sqrt((xx[i]-xx[j])*(xx[i]-xx[j])+(yy[i]-yy[j])*(yy[i]-yy[j]));//建边(双边权)
b[j][i]=b[i][j];
a[i][j]=abs(zz[i]-zz[j]);
a[j][i]=a[i][j];
}
}
long double l=0,r=1e5;
while(r-l>=0.0001)//二分,注意精度限制
{
long double mid=(l+r)/2,pp=prim(mid);
if(pp==1)//Min>0
l=mid;
if(pp==0)//Min=0
{
ans=mid;
break;
}
if(pp==-1)//Min<0
{
ans=min(ans,mid);
r=mid;
}
}
printf("%.3Lf\n",ans);
}
return 0;
}
最小乘积生成树
这一题的边上依然是两个边权,要维护两个边权\(a\)和\(b\)各自加和后乘积的最小值。
这个应该怎么做呢?
我们有一个贪心算法,就是按照其中一个权值排序,去做Kruskal算法,但是明显对于这一题来说是不正确的做法。
我们可以把每一棵生成树的两个权值之和看成一个坐标(x,y),我们想要的答案就一定在凸壳上面(如果不在凸壳上的点一定可以被一个横坐标和纵坐标都比自己小的点所替代)。
如图:红色的点为被淘汰的点,蓝色的点为凸壳上的点。
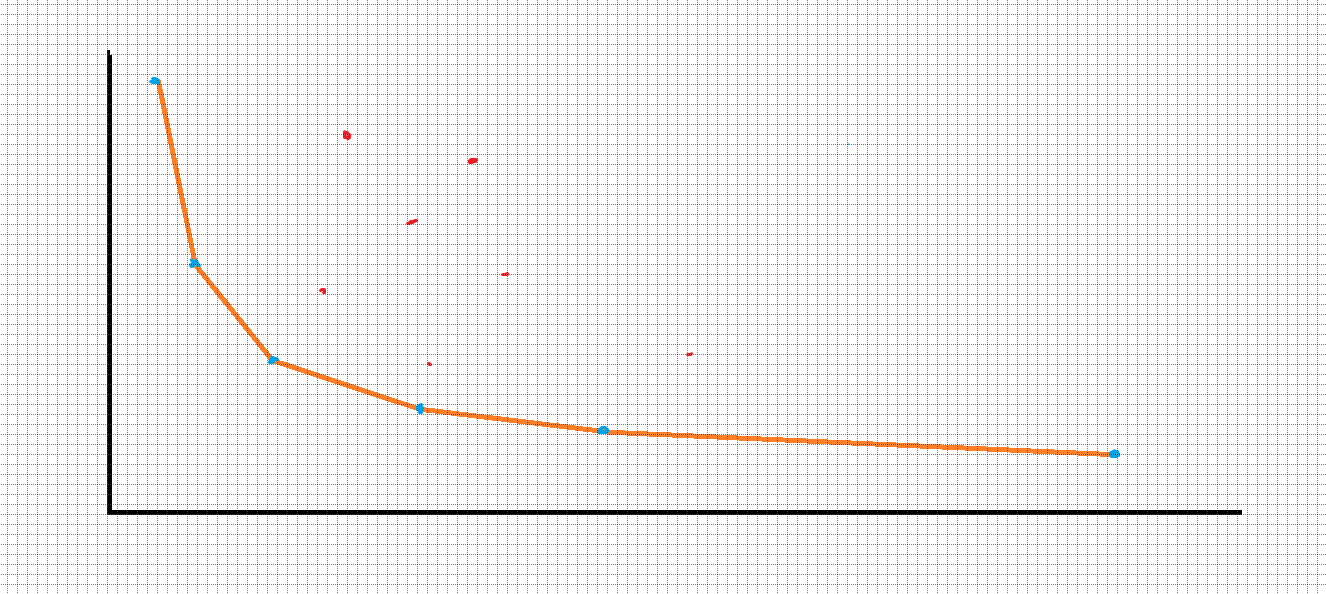
如何找出凸壳上的点呢?
我们可以用一种分治的方式,先分别按权值\(a\)排序,求出凸壳最上端的点\(X_1\),再按照权值\(b\)排序,求出凸壳最下端的点\(X_2\)。
然后找出距离这两个连线距离最远的且在连线下面的点\(X_3\),然后再分治,求出距离\(X_1\)与\(X_3\)连线距离最远的且在连线下面的点\(X_4\)以及距离\(X_2\)与\(X_3\)连线距离最远的且在连线下面的点\(X_5\),不断递归下去做。
如何寻找距离两个点连线最远且在连线下面呢?我们可以把距离转化面积,即求面积最大的点,可以用向量的叉积求解。
数学补习:向量的叉积
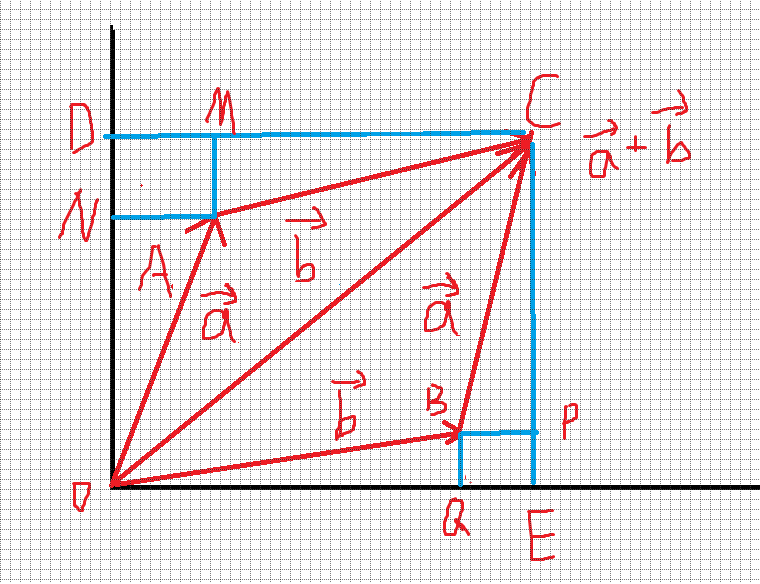
向量的叉积\(\vec{a} \times \vec{b}=S_{▱OACB}\)
我们假设\(\vec{a}=(x1,y1)\),\(\vec{b}=(x2,y2)\),\(\vec{a}+\vec{b}=(x1+x2,y1+y2)\)
\(S_{▱OACB}=S_{▭ODCE}-S_{∆AMC}-S_{∆OBQ}-S_{∆CBP}-S_{∆AON}-S_{▭AMDN}-S_{▭BQEP}\)
\(\vec{a} \times \vec{b}=(x_1+x_2)(y_1+y_2) -\frac {1}{2} x_2 y_2 -\frac {1}{2} x_2 y_2 - \frac {1}{2} x_1 y_1 - \frac {1}{2} x_1 y_1 - x_1 y_2 - x_1 y_2=x_2 y_1- x_1 y_2\)
因此,\(\vec{a} \times \vec{b} =x_2 y_1 - x_1 y_2\)
回到原题。
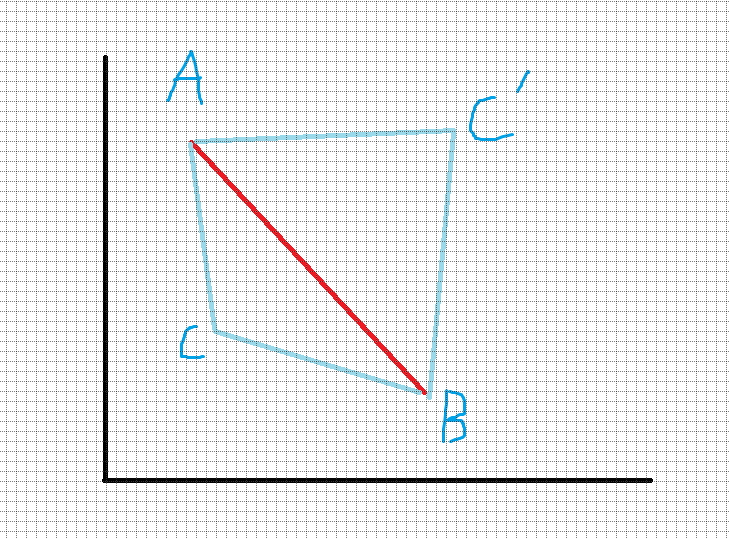
我们注意到我们要求的\(C\)点满足\(\vec{CA} \times \vec{CB}\)最大(图上还有一个\(C'\)点,请注意\(\vec{CA} \times \vec{CB}\)和\(\vec{C'A} \times \vec{C'B}\)的正负是不一样的,可以通过这个排除线段\(AB\)以上的点)
我们一开始是可以找出凸包的两端点,然后要维护一颗生成树使得\(\vec{CA} \times \vec{CB}\)最大,也就是使得\(x_{\vec{CB}} y_{\vec{CA}}-x_{\vec{CA}} y_{\vec{CB}}\)最大,我们设\(x_{\vec{CB}} y_{\vec{CA}}-x_{\vec{CA}} y_{\vec{CB}}=m\)
\(m=(x_B-x_C)(y_A-y_C)-(x_C-x_A)(y_C-y_B)=x_B y_A-x_B y_C -x_C y_A -x_A y_B +x_C y_B +x_A y_C=x_C(y_B-y_A)+(x_A-x_B)y_C+x_B y_A-x_A y_B\)
注意到\(t=x_B y_A-x_A y_B\)是一个常数,不会影响到\(C\)点坐标的求解,我们可以忽略。
因此,\(m=x_C(y_B-y_A)+(x_A-x_B)y_C+t\)
我们要维护\(m\)最大,也就是维护\(-m=x_C(y_A-y_B)+(x_B-x_A)y_C-t\)最小。
我们以\(a[i] \times (y_A-y_B) +b[i] \times (x_B-x_A)\)作为每一条边的权值去跑一遍做小生成树就可以求出\(C\)点的坐标了,记得更新答案。
算法流程:
1.以\(a[i]\)作为边权跑最小生成树,求出凸壳最上端的点,以\(b[i]\)作为边权跑最小生成树,求出凸壳最下端的点。
2.以两个端点\(A\)和\(B\)作为递归起点,每次以\(a[i] \times (y_A-y_B) +b[i] \times (x_B-x_A)\)作为边权跑最小生成树,求出中间点\(C\),然后再分别以\(AC\)和\(BC\)作为端点,重复过程2,直到无法找到中间点。
Code:
#include<bits/stdc++.h>
#define maxn 250000
using namespace std;
struct bian
{
int x,y,a,b,v;
const bool operator <(const bian &xx1)
{
return v<xx1.v;
}
}q[maxn];
int n,m,f[maxn],ans=1e9,ans1=1e9,ans2=1e9;
int find(int x)
{
if(x==f[x])return x;
else return f[x]=find(f[x]);
}
int mst(int &x,int &y)//kruskal板子,注意x,y带了取址符,可以直接返回坐标
{
x=y=0;
sort(q+1,q+m+1);
for(int i=1;i<=n;i++)f[i]=i;
for(int i=1;i<=m;i++)
{
int fx=find(q[i].x),fy=find(q[i].y);
if(fx==fy)continue;
f[fx]=fy;
x+=q[i].a,y+=q[i].b;
}
if(x*y==ans&&x<ans1)ans=x*y,ans1=x,ans2=y;//更新答案
if(x*y<ans)ans=x*y,ans1=x,ans2=y;
}
int dfs(int ax,int ay,int bx,int by)
{
for(int i=1;i<=m;i++)q[i].v=(ay-by)*q[i].a+(bx-ax)*q[i].b;//边权赋值
int rx,ry;
mst(rx,ry);//跑最小生成树,求出中间点的坐标
if((ay-by)*rx+(bx-ax)*ry-bx*ay+ax*by<0)dfs(ax,ay,rx,ry),dfs(rx,ry,bx,by);//如果还能继续递归,则递归下去
}
int main()
{
scanf("%d%d",&n,&m);
for(int i=1;i<=m;i++)
scanf("%d%d%d%d",&q[i].x,&q[i].y,&q[i].a,&q[i].b),q[i].x++,q[i].y++;
for(int i=1;i<=m;i++)q[i].v=q[i].a;
int ax,ay,bx,by;
mst(ax,ay);
for(int i=1;i<=m;i++)q[i].v=q[i].b;
mst(bx,by);
dfs(ax,ay,bx,by);
printf("%d %d\n",ans1,ans2);
return 0;
}
最小差值生成树
前置知识:LCT维护动态最小生成树
差值最小,那么最大值固定时,最小值要最大。
按边权排序,然后从小到大加边。然后用一个指针指向未被删除的最小边。
每次加边查询是否连通,没连通直接加,
否则查询路径上的边,把它删了,打个删除标记,然后加上当前边。
用当前边减去最小边更新答案。
注意:原题有自环!
Code:
#include<bits/stdc++.h>
#define maxn 900000
using namespace std;
int c[maxn][2],fa[maxn],v[maxn],mx[maxn],xm[maxn];
bool rlz[maxn];
bool nroot(int x){return c[fa[x]][0]==x||c[fa[x]][1]==x;}
void pushup(int x)
{
mx[x]=max(max(mx[c[x][0]],mx[c[x][1]]),v[x]);
if(c[x][0]&&mx[x]==mx[c[x][0]])
xm[x]=xm[c[x][0]];
else if(mx[x]==v[x])
xm[x]=x;
else
xm[x]=xm[c[x][1]];
}
void rev(int x)
{
swap(c[x][0],c[x][1]);
rlz[x]^=1;
}
void pushdown(int x)
{
if(!rlz[x])
return ;
if(c[x][0])
rev(c[x][0]);
if(c[x][1])
rev(c[x][1]);
rlz[x]=0;
}
void rotate(int x)
{
int y=fa[x],z=fa[y],k=(c[y][1]==x),w=c[x][!k];
if(nroot(y))
c[z][c[z][1]==y]=x;
c[x][!k]=y,c[y][k]=w;
if(w)
fa[w]=y;
fa[y]=x;fa[x]=z;
pushup(y);
}
void pushtag(int x)
{
if(nroot(x))
pushtag(fa[x]);
pushdown(x);
}
void splay(int x)
{
pushtag(x);
while(nroot(x))
{
int y=fa[x],z=fa[y];
if(nroot(y))
rotate((c[y][0]==x)^(c[z][0]==y)?x:y);
rotate(x);
}
pushup(x);
}
int Pre(int x)
{
splay(x);
x=c[x][0];
while(c[x][1])
x=c[x][1];
return x;
}
int Nxt(int x)
{
splay(x);
x=c[x][1];
while(c[x][0])
x=c[x][0];
return x;
}
void access(int x)
{
for(int y=0;x;x=fa[y=x])
splay(x),c[x][1]=y,pushup(x);
}
void makeroot(int x){access(x);splay(x);rev(x);}
int findroot(int x)
{
access(x);splay(x);
while(c[x][0])
x=c[x][0];
splay(x);
return x;
}
void split(int x,int y){makeroot(x);access(y);splay(y);}
int Max(int x,int y)
{
split(x,y);
return mx[y];
}
int Xam(int x,int y)
{
split(x,y);
return xm[y];
}
void cut(int x,int y)
{
makeroot(x);
if(findroot(y)==x&&fa[y]==x&&!c[x][0])
fa[y]=c[x][1]=0;
}
void lk(int x,int y)
{
makeroot(x);
fa[x]=y;
}
int link(int x,int y,int nw)
{
makeroot(x);
if(findroot(y)!=x)
return lk(x,nw),lk(nw,y),0;
else
{
if(v[nw]>=Max(x,y))
return -1;
int ct=Xam(x,y),pr=Pre(ct),nx=Nxt(ct);
cut(ct,pr);cut(ct,nx);
lk(x,nw);lk(y,nw);
return ct;
}
}
struct ljq
{
int u,v,w;
}e[maxn];
int val[maxn],ans=1e9;
bool cmp(ljq xx1,ljq xx2){return xx1.w>xx2.w;}
int n,m;
int main()
{
scanf("%d%d",&n,&m);
for(int i=1;i<=m;i++)
scanf("%d%d%d",&e[i].u,&e[i].v,&e[i].w);
sort(e+1,e+m+1,cmp);
for(int i=1;i<=m;i++)
v[n+i]=mx[n+i]=e[i].w;
for(int i=1;i<=n+m;i++)
xm[i]=i;
int p=0,last=1;
for(int i=1;i<=m;i++)
{
if(e[i].u==e[i].v)
{
val[i]=1;
continue;
}
int t=link(e[i].u,e[i].v,n+i);
if(t==0)
p++;
if(t==-1)
val[i]=1;
if(t>0)
{
t-=n;
val[t]=1;
if(last==t)
while(val[last])
last++;
}
if(p==n-1)
ans=min(ans,e[last].w-e[i].w);
}
printf("%d\n",ans);
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号