[BZOJ4558/LOJ2025/Luogu3271][GZOI2016/JLOI2016/SHOI2016]方
题目链接:
一个简单的容斥题(然后自己卡住一直没出来)
首先不考虑“坏点”,那么如何计算正方形个数呢?
换一种思路,枚举正好包住正方形的正方形大小(有点拗口),再统计里面有多少个正好在此正方形上的正方形。
如图,此时枚举的正方形为\(EFGH\),边长为\(i\),统计有多少正方形顶点“贴”在此正方形上。
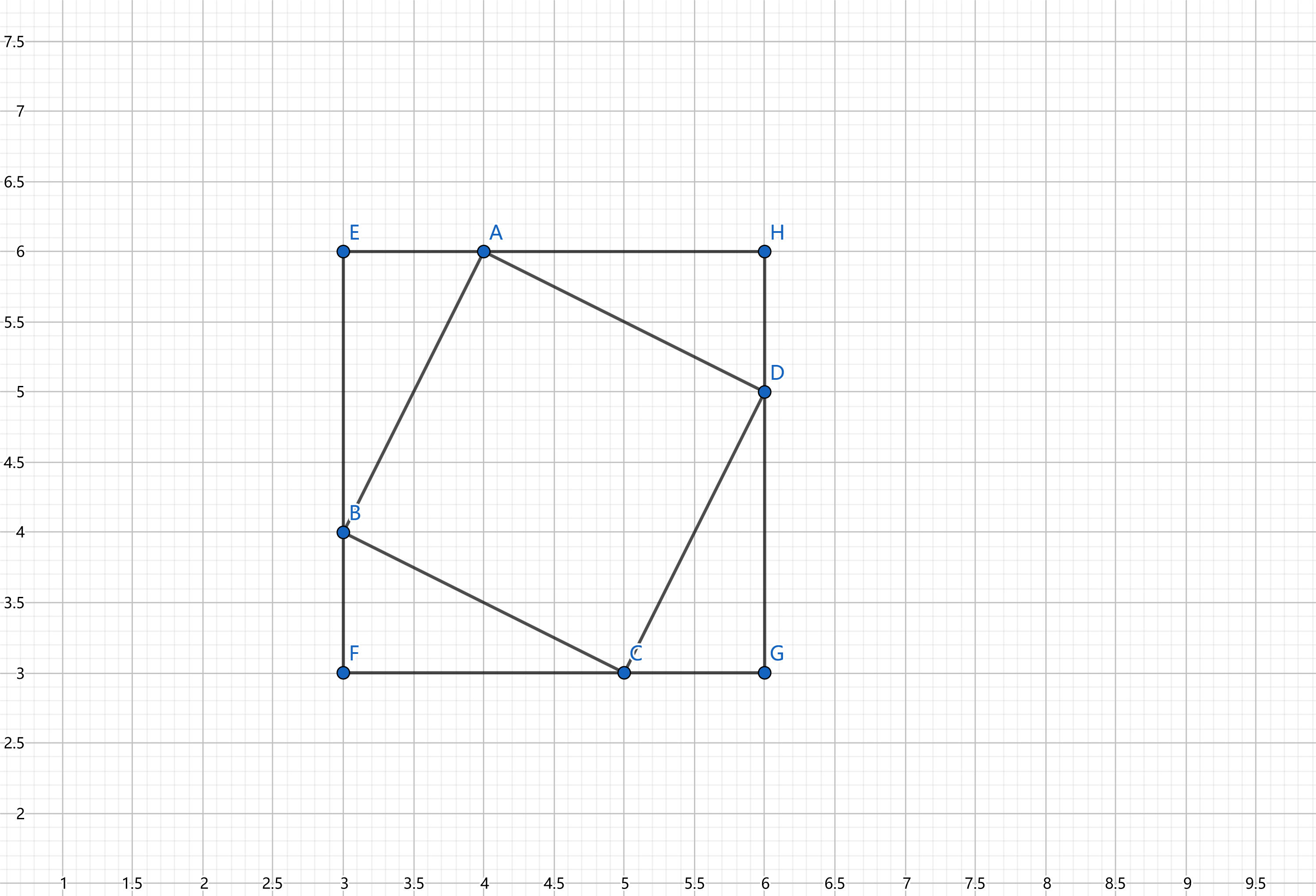
那么对于一个点\(A\),可以和一条边上的\(i\)个点对应,那么就有\(i\)种正方形。
边长为\(i\)的\(EFGH\)有多少个?当然是\((n-i+1)*(m-i+1)\)个了~。
于是初始答案即为\(\sum_{i=1}^{\min(n,m)}i*(n-i+1)*(m-i+1)\)
对此可以\(O(n)\)地计算(其实还有\(O(log)\)的方法)
接着对于坏点,首先统计有多少正方形至少在一个“坏点”上。
那么对于一个点\(A(x,y)\),只需分别统计其对于正上方,正下方,左方和右方的贡献,最后减去重叠的部分即可。
若点\(A(x,y)\)在正方形\(ABCD\)上,那么就会有一个正方形\(EFGH\)正好包含\(ABCD\)。
若现在统计对于正上方的贡献,那么\(A\)就在\(EFGH\)的底边上。

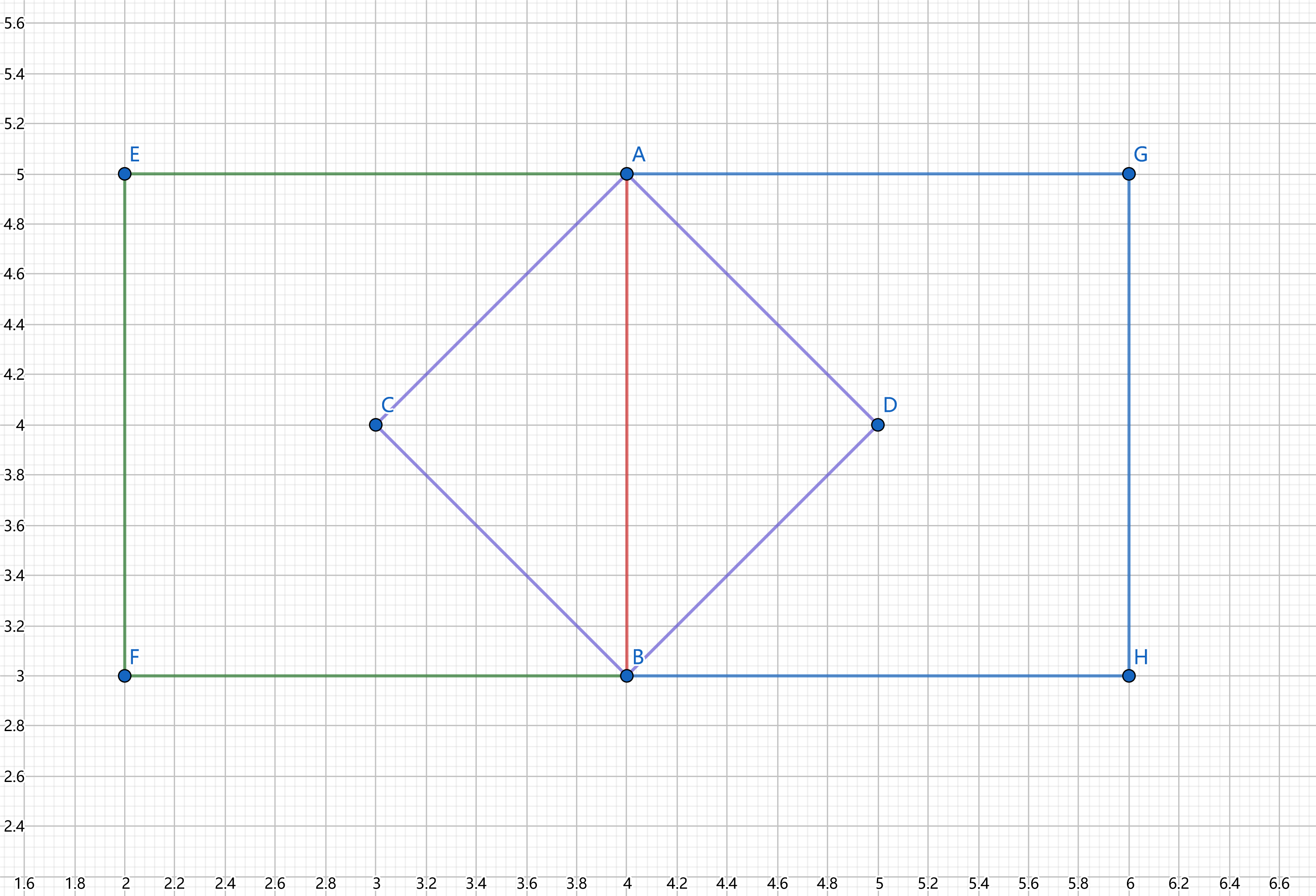
如图,\(P1\sim P4\)为整个网格图。
若\(EFGH\)的边长为\(i\),则\(i\)的取值范围就是\([1,t=\min(AB,AC+AD)]\),此时\(EFGH\)有\(i+1\)种选法(\(A\)与底边\(i+1\)个点一一对应)。
若\(t\le AC\)且\(t\le AD\),那么方案数就是\(\sum_{i=1}^t (i+1)=\frac{t(t+3)}2\)。
若\(t>AC\),那么就要把超出去的给剪掉。
若\(t-AC=a\),那么就要减去\(\frac{a(a+1)}2\)。
\(t>AD\)同理。
对于其他三个方向同理。
最后要减去四个方向的重叠部分(也就是一个点是\(A\)的\(EFGH\))
那么对于正上方和左方,重复的个数就是\(\min(AB,AC)\)(\(EFGH\)以\(A\)为右下角,向左上延伸)。
其他的重叠同理。
接着你会发现统计完\(1\)个"坏点"之后,这样会重复统计\(2\)个坏点的正方形,那么继续容斥,加上\(2\)个的,再减\(3\)个的,最后加上\(4\)个点全是坏点的正方形个数。
至于如何统计这些,可以枚举正方形的两个点,分\(3\)种情况求出正方形,如下图。
求出另外两个点判断是否存在即可。
注意这样会重复统计,最后\(3\)个的要除以\(C_3^2\),\(4\)个的除以\(C_4^2\)(有多少种方案统计此正方形)。
如何判断存在?你可以用\(set\)或者二分,我这里用了\(Hash\)表,乐观情况下是\(O(1)\)的。
于是上面的步骤时间复杂度为\(O(k^2)/O(k^2log_2k)\)
那么这题就愉快地做完了。
代码:
#include <cstdio>
typedef long long ll;
inline int Abs(const int x){return x>=0?x:-x;}
inline int Min(const int a,const int b){return a<b?a:b;}
inline int Max(const int a,const int b){return a>b?a:b;}
int n,m,k,xs[2005],ys[2005];
const int Mod=100000007;
struct Hash_Table//哈希表
{
int Head[1000005],Next[2005],Vx[2005],Vy[2005],En;
inline void Insert(const int x,const int y)
{
int Hv=x*1LL*y%1000003;
Next[++En]=Head[Hv];
Head[Hv]=En;
Vx[En]=x,Vy[En]=y;
}
bool Find(const int x,const int y)
{
int Hv=x*1LL*y%1000003;
for(int i=Head[Hv];i;i=Next[i])
if(Vx[i]==x&&Vy[i]==y)
return true;
return false;
}
}Map;
int Get(int l,int r,int h)
//求一个坏点一个方向的贡献
//AB=h,AC=l,AD=r
{
int t=Min(h,l+r);
int Res=t*(t+3LL)/2%Mod;
if(t>l)Res=(Res-(t-l)*(t-l+1LL)/2)%Mod;
if(t>r)Res=(Res-(t-r)*(t-r+1LL)/2)%Mod;
return (Res+Mod)%Mod;
}
int C2,C3,C4;
//坏点数为2,3,4的正方形数量
inline void Check(int ax,int ay,int bx,int by)
//正方形另外两点为(ax,ay),(bx,by),进行统计
{
if(ax<0||ax>n||ay<0||ay>m)return;
if(bx<0||bx>n||by<0||by>m)return;
//不合法情况
int Cnt=0;
if(Map.Find(ax,ay))++Cnt;
if(Map.Find(bx,by))++Cnt;
++C2;
if(Cnt>=1)++C3;
if(Cnt>=2)++C3,++C4;
//分别累积
}
int main()
{
scanf("%d%d%d",&n,&m,&k);
int Ans=0;
for(int i=1;i<=Min(n,m);++i)
Ans=(Ans+(n-i+1LL)*(m-i+1)%Mod*i)%Mod;//初始的方案数
for(int i=1;i<=k;++i)
{
scanf("%d%d",&xs[i],&ys[i]);
Map.Insert(xs[i],ys[i]);
int a=xs[i],b=ys[i],c=n-a,d=m-b;
int Cnt=((ll)Get(a,c,b)+Get(a,c,d)+Get(b,d,a)+Get(b,d,c))%Mod;
//四个方向的贡献
Cnt=(Cnt-Min(a,b)-Min(b,c)-Min(c,d)-Min(a,d))%Mod;
//容斥掉重复部分
Ans=(Ans-Cnt)%Mod;
}
for(int i=1;i<k;++i)
for(int j=i+1;j<=k;++j)
{
int dx=xs[i]-xs[j],dy=ys[i]-ys[j];
Check(xs[i]+dy,ys[i]-dx,xs[j]+dy,ys[j]-dx);
Check(xs[i]-dy,ys[i]+dx,xs[j]-dy,ys[j]+dx);
//(i,j)两点为正方形一边。
if((Abs(dx)+Abs(dy))&1)continue;
//不能当对角线
int nx=(dx-dy)>>1,ny=(dx+dy)>>1;
Check(xs[i]-nx,ys[i]-ny,xs[j]+nx,ys[j]+ny);
//这里的式子很简单就不说了
}
printf("%lld\n",(((ll)Ans+C2-C3/3+C4/6)%Mod+Mod)%Mod);
//Final容斥
return 0;
}

