2012Noip提高组Day1 T3 开车旅行
小 A 和小 B 决定利用假期外出旅行,他们将想去的城市从 1 到 N 编号,且编号较小的
城市在编号较大的城市的西边,已知各个城市的海拔高度互不相同,记城市 i 的海拔高度为
Hi,城市 i 和城市 j 之间的距离 d[i,j]恰好是这两个城市海拔高度之差的绝对值,即
d[i,j] = |Hi− Hj|。
旅行过程中,小 A 和小 B 轮流开车,第一天小 A 开车,之后每天轮换一次。他们计划
选择一个城市 S 作为起点,一直向东行驶,并且最多行驶 X 公里就结束旅行。小 A 和小 B
的驾驶风格不同,小 B 总是沿着前进方向选择一个最近的城市作为目的地,而小 A 总是沿
着前进方向选择第二近的城市作为目的地(注意:本题中如果当前城市到两个城市的距离
相同,则认为离海拔低的那个城市更近)。如果其中任何一人无法按照自己的原则选择目的
城市,或者到达目的地会使行驶的总距离超出 X 公里,他们就会结束旅行。
在启程之前,小 A 想知道两个问题:
1.对于一个给定的 X=X0,从哪一个城市出发,小 A 开车行驶的路程总数与小 B 行驶
的路程总数的比值最小(如果小 B 的行驶路程为 0,此时的比值可视为无穷大,且两个无穷大视为相等)。如果从多个城市出发,小 A 开车行驶的路程总数与小 B 行驶的路程总数的比
值都最小,则输出海拔最高的那个城市。
- 对任意给定的 X=Xi和出发城市 Si,小 A 开车行驶的路程总数以及小 B 行驶的路程
总数。
输入输出格式
输入格式: 
第一行包含一个整数 N,表示城市的数目。
第二行有 N 个整数,每两个整数之间用一个空格隔开,依次表示城市 1 到城市 N 的海
拔高度,即 H1,H2,……,Hn,且每个 Hi都是不同的。
第三行包含一个整数 X0。
第四行为一个整数 M,表示给定 M 组 Si和 Xi。
接下来的 M 行,每行包含 2 个整数 Si和 Xi,表示从城市 Si出发,最多行驶 Xi公里。
输出格式:
输出共 M+1 行。
第一行包含一个整数 S0,表示对于给定的 X0,从编号为 S0的城市出发,小 A 开车行驶
的路程总数与小 B 行驶的路程总数的比值最小。
接下来的 M 行,每行包含 2 个整数,之间用一个空格隔开,依次表示在给定的 Si和
Xi下小 A 行驶的里程总数和小 B 行驶的里程总数。
输入输出样例
drive1 4 2 3 1 4 3 4 1 3 2 3 3 3 4 3 drive2 10 4 5 6 1 2 3 7 8 9 10 7 10 1 7 2 7 3 7 4 7 5 7 6 7 7 7 8 7 9 7 10 7
drive1 1 1 1 2 0 0 0 0 0 drive2 2 3 2 2 4 2 1 2 4 5 1 5 1 2 1 2 0 0 0 0 0
说明
【输入输出样例 1 说明】
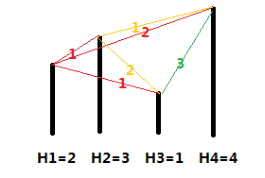
各个城市的海拔高度以及两个城市间的距离如上图所示。
如果从城市 1 出发,可以到达的城市为 2,3,4,这几个城市与城市 1 的距离分别为 1,1,2,
但是由于城市 3 的海拔高度低于城市 2,所以我们认为城市 3 离城市 1 最近,城市 2 离城市
1 第二近,所以小 A 会走到城市 2。到达城市 2 后,前面可以到达的城市为 3,4,这两个城
市与城市 2 的距离分别为 2,1,所以城市 4 离城市 2 最近,因此小 B 会走到城市 4。到达城
市 4 后,前面已没有可到达的城市,所以旅行结束。
如果从城市 2 出发,可以到达的城市为 3,4,这两个城市与城市 2 的距离分别为 2,1,由
于城市 3 离城市 2 第二近,所以小 A 会走到城市 3。到达城市 3 后,前面尚未旅行的城市为
4,所以城市 4 离城市 3 最近,但是如果要到达城市 4,则总路程为 2+3=5>3,所以小 B 会
直接在城市 3 结束旅行。
如果从城市 3 出发,可以到达的城市为 4,由于没有离城市 3 第二近的城市,因此旅行
还未开始就结束了。
如果从城市 4 出发,没有可以到达的城市,因此旅行还未开始就结束了。
【输入输出样例 2 说明】
当 X=7 时,
如果从城市 1 出发,则路线为 1 -> 2 -> 3 -> 8 -> 9,小 A 走的距离为 1+2=3,小 B 走的
距离为 1+1=2。(在城市 1 时,距离小 A 最近的城市是 2 和 6,但是城市 2 的海拔更高,视
为与城市 1 第二近的城市,所以小 A 最终选择城市 2;走到 9 后,小 A 只有城市 10 可以走,
没有第 2 选择可以选,所以没法做出选择,结束旅行)
如果从城市 2 出发,则路线为 2 -> 6 -> 7 ,小 A 和小 B 走的距离分别为 2,4。
如果从城市 3 出发,则路线为 3 -> 8 -> 9,小 A 和小 B 走的距离分别为 2,1。
如果从城市 4 出发,则路线为 4 -> 6 -> 7,小 A 和小 B 走的距离分别为 2,4。
如果从城市 5 出发,则路线为 5 -> 7 -> 8 ,小 A 和小 B 走的距离分别为 5,1。
如果从城市 6 出发,则路线为 6 -> 8 -> 9,小 A 和小 B 走的距离分别为 5,1。
如果从城市 7 出发,则路线为 7 -> 9 -> 10,小 A 和小 B 走的距离分别为 2,1。
如果从城市 8 出发,则路线为 8 -> 10,小 A 和小 B 走的距离分别为 2,0。
如果从城市 9 出发,则路线为 9,小 A 和小 B 走的距离分别为 0,0(旅行一开始就结
束了)。
如果从城市 10 出发,则路线为 10,小 A 和小 B 走的距离分别为 0,0。
从城市 2 或者城市 4 出发小 A 行驶的路程总数与小 B 行驶的路程总数的比值都最小,
但是城市 2 的海拔更高,所以输出第一行为 2。
【数据范围】
对于 30%的数据,有 1≤N≤20,1≤M≤20;
对于 40%的数据,有 1≤N≤100,1≤M≤100;
对于 50%的数据,有 1≤N≤100,1≤M≤1,000;
对于 70%的数据,有 1≤N≤1,000,1≤M≤10,000;
对于100%的数据,有1≤N≤100,000,1≤M≤10,000,-1,000,000,000≤Hi≤1,000,000,000,
0≤X0≤1,000,000,000,1≤Si≤N,0≤Xi≤1,000,000,000,数据保证 Hi互不相同。
很显然我们需要一个比n^2暴力找最近第二近城市的更优的算法。
我们可以用链表,把城市按高度从低到高排序,然后相邻的城市连起来,然后我们从原来城市编号里,从第一个城市开始寻找,很明显对于原来标号为i的城市,在排序后里面,它的最近和第二近的城市就是它排序后所在位置向左两个(i-1,i-2)到向右两个(i+1,i+2)这四个城市中的两个,找完之后这个城市i就可以删掉了(因为开车要一路向东,编号是递增的,所以可以删掉已经找完的),然后再把i-1和i+1连起来就可以了。
之后我们还可以发现其实对于一个起点来说,它怎么走是已经确定了的,相比我们一步一步模拟地走,我们可以采取倍增的方法,多步多步地走就可以更优了。
我们可以把A,B各行动一次作为一次行动,然后最后再判一次A能不能再走一次就可以了。

1 #include <cstring> 2 #include <cstdio> 3 #include <iostream> 4 #include <algorithm> 5 #define N 100005 6 using namespace std; 7 struct data{ 8 int hi,sign; 9 }city[N]; 10 int n,m,x,y,num,x0,f[N][20],pre[N],next[N],fir[N],sec[N],head[N]; 11 double qwq,ans; 12 long long a[N][20],b[N][20]; 13 bool cmp(const struct data a,const struct data b){ 14 return (a.hi<b.hi); 15 } 16 void solve(int x){ 17 fir[x]=(pre[x]&&(city[x].hi-city[pre[x]].hi<=city[next[x]].hi-city[x].hi||!next[x]))?pre[x]:next[x]; 18 if (fir[x]==pre[x]) 19 sec[x]=(pre[pre[x]]&&(city[x].hi-city[pre[pre[x]]].hi<=city[next[x]].hi-city[x].hi||!next[x]))?pre[pre[x]]:next[x]; 20 else sec[x]=(pre[x]&&(city[x].hi-city[pre[x]].hi<=city[next[next[x]]].hi-city[x].hi||!next[next[x]]))?pre[x]:next[next[x]]; 21 pre[next[x]]=pre[x]; 22 next[pre[x]]=next[x]; 23 } 24 void work(int u,int x0){ 25 for (int i=19;i>=0;i--) 26 if ((f[u][i])&&(x0-a[u][i]-b[u][i]>=0)){ 27 x+=a[u][i]; 28 y+=b[u][i]; 29 x0=x0-a[u][i]-b[u][i]; 30 u=f[u][i]; 31 } 32 if ((x0-a[u][0]>=0)&&(sec[u])){ 33 x+=a[u][0]; 34 u=sec[u]; 35 } 36 } 37 int main(){ 38 scanf("%d",&n); 39 for (int i=1;i<=n;++i){ 40 scanf("%d",&city[i].hi); 41 city[i].sign=i; 42 } 43 sort(city+1,city+1+n,cmp); 44 for (int i=1;i<=n;++i){ 45 head[city[i].sign]=i; 46 pre[i]=i-1; 47 next[i]=i+1; 48 if (i==n) next[i]=0; 49 } 50 for (int i=1;i<=n;i++) 51 solve(head[i]); 52 for (int i=1;i<=n;++i){ 53 f[i][0]=fir[sec[i]]; 54 a[i][0]=abs(city[i].hi-city[sec[i]].hi); 55 b[i][0]=abs(city[sec[i]].hi-city[fir[sec[i]]].hi); 56 } 57 for (int j=1;j<=19;++j) 58 for (int i=1;i<=n;++i){ 59 f[i][j]=f[f[i][j-1]][j-1]; 60 a[i][j]=a[i][j-1]+a[f[i][j-1]][j-1]; 61 b[i][j]=b[i][j-1]+b[f[i][j-1]][j-1]; 62 } 63 scanf("%d",&x0); 64 ans=1<<30;num=0; 65 for (int i=1;i<=n;++i){ 66 x=y=qwq=0; 67 work(head[i],x0); 68 if (y==0) qwq=1<<31-1; 69 else qwq=(double)x/(double)y; 70 if ((ans>qwq)||(ans==qwq&&city[head[num]].hi<city[i].hi)){ 71 ans=qwq; 72 num=i; 73 } 74 } 75 printf("%d\n",num); 76 scanf("%d",&m); 77 int qaq; 78 while (m--){ 79 x=y=0; 80 scanf("%d%d",&qaq,&x0); 81 work(head[qaq],x0); 82 printf("%d %d\n",x,y); 83 } 84 return 0; 85 }
n^2暴力预处理最近第二近的然后暴力跑跑什么的也有50、70分也好良心啊.......



 浙公网安备 33010602011771号
浙公网安备 33010602011771号