树链剖分小结
一直认为树链剖分是个很玄学的东西,发现实质后原来是如此的简单。
顾名思义,树链剖分就是将树剖成一条条链,然后用数据结构维护。
我们常用的自然就是线段树。
我们可以知道dfs序是能够反映树上的点连续的信息的。
所以链就是dfs序。
但这个dfs序又不普通。
我们知道,在dfs序里,被许多点分成了好多段。
比如这里有一棵树:
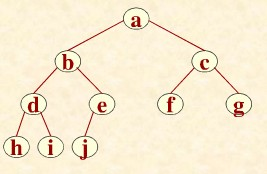
我们假设它的dfs序为:abdhiejcfg
那么对于一条路径a-h,它的dfs序是连续的,如果我们要更改他们的信息,我们就很好的利用了线段树区间修改的优点。
但如果我们要更改i-g的信息,我们发现这条路径 i-d-b-a-c-g 在dfs序中并不连续,甚至在这里我们必须单点修改!完全没有发挥线段树区间维护的优势。
在这里我们得到了一个启示,我们尽量要让尽可能多的点在dfs序中连续,这样我们修改时才会尽可能地发挥线段树区间维护的优势,很幸运,我们可以做到——启发式划分!
这个就是重儿子轻儿子的概念。
重儿子:以该儿子为根的子树所含节点数是其他儿子中最多的。
轻儿子:除重儿子之外就是轻儿子啦。
所以我们在DFS中,优先搜索重儿子,这样,我们就能让更多的节点在dfs序中连续。
自然而然,连接重儿子的链就是重链。
连接轻儿子的链就是轻链。
搜索完后,我们需要对dfs序进行划分区域。
我们运用top[i]表示i所在重链链的深度最浅的节点编号。
对于轻链上的点i的top[i]就是它本身i
同时用id[i]表示i节点在dfs序中的位置。
这样,id[top[i]]~id[i]的区间就是一条链上的点了。
区域就成功划分了,那我们如何进行修改呢??
假设这里又有一棵树:
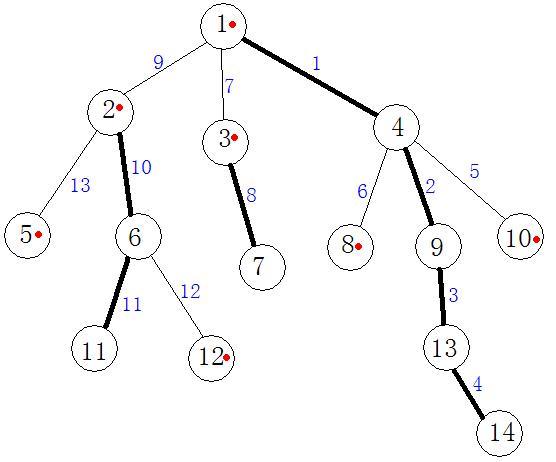
其中粗边就是重链,细边就是轻链。
它的dfs序为:1 4 9 13 14 8 10 3 7 2 6 11 5 12
假设我们需要对11-10路径上的点的权值都加1。
我们定位到id[11]=12,id[10]=7;
同时top[11]=2,top[10]=10
我们优先修改top点深度深的的信息。
我们发现它就是11号点那里。
它是在重链上,我们可以知道top[11]-11点在dfs序上是连续的,于是我们可以直接修改这一段区间的信息,都让它们加1.
为方便叙述,a=11,b=10。
修改完后,a=fa[top[a]]=1,其中fa[i]表示i的父亲
此时top[a]=1,再次比较top[a]和top[b]的深度,我们决定要修改b
于是我们更改了id[top[b]]-id[b]的信息,实际上就是b这个点的信息。
然后b=fa[top[b]]=4,此时top[b]=1;
我们发现此时top[a]=top[b],那么我们就更改id[a]-id[b]区间的信息即可。
求和的操作类似于上。
到现在我们发现,树链剖分实际上也不是什么玄学玩意,它就是一棵线段树加上一个从树转成序列的操作罢了。
而这个操作,我们就运用了top数组 id数组进行区域划分,fa数组进行转移,deep数组进行判断优先更改谁。
如果我们需要更改以某一节点为根的所有子树的信息,那么我们再加上一个数组size,表示以某节点i为根节点的子树的节点个数(包括它自己),那么在dfs序中,这棵子树所在的区间就是 id[i]~id[i]+size[i]-1
具体实现方法如下:
我们分两次DFS
第一次DFS统计出节点i的重儿子son[i],节点的深度deep[i],以该节点为根的子树的节点个数size[i]
第二次DFS划分出重轻链,重儿子优先记录dfs序该节点的top[i]和id[i]。
然后,我们根据dfs序建立一棵线段树。
然后对于修改x-y的路径上的节点权值。
我们令f1=top[x],f2=top[y];
当f1不等于f2时我们开始循环
同时我们要保证deep[f1]>deep[f2]
若大于则交换,然后我们就更改id[f1]~id[x]的信息
然后x=fa[f1],f1=top[x];
若f1仍不等于f2,重复上面步骤,直到f1=f2为止
如果x=y,那么我们就直接更改id[x]
否则就更改id[y]~id[x]的区间(此时deep[x]>deep[y])
查询类似上述操作,可自己想想以加深对树链剖分的理解。
剖分后的树有如下性质:
性质1:如果(v,u)为轻边,则siz[u] * 2 < siz[v];
性质2:从根到某一点的路径上轻链、重链的个数都不大于logn。

1 #include <iostream> 2 #include <cstdio> 3 #include <cstring> 4 #include <algorithm> 5 #include <cmath> 6 #define N 500005 7 #define M 100005 8 using namespace std; 9 struct data1{ 10 int min,max,mark; 11 long long sum; 12 }tree[N]; 13 struct data2{ 14 int next,to,power; 15 }line[M*2]; 16 int num,head[M],deep[M],f[M],son[M],top[M],size[M],val[M],dfn[M],id[M],n,m,r,p,ans,t,a,b,c,d; 17 void add(int u,int v){ 18 num++; 19 line[num].next=head[u]; 20 line[num].to=v; 21 head[u]=num; 22 num++; 23 line[num].next=head[v]; 24 line[num].to=u; 25 head[v]=num; 26 } 27 void dfs1(int x,int fa){ 28 f[x]=fa; 29 deep[x]=deep[fa]+1; 30 size[x]=1; 31 for (int v,i=head[x];i;i=line[i].next){ 32 v=line[i].to; 33 if (v!=fa){ 34 dfs1(v,x); 35 size[x]+=size[v]; 36 if ((son[x]==-1)||(size[v]>size[son[x]])) 37 son[x]=v; 38 } 39 } 40 } 41 void dfs2(int x,int fa){ //这里的fa指的是top[x] 42 dfn[++t]=x; 43 id[x]=t; 44 top[x]=fa; 45 if (son[x]==-1) return; 46 dfs2(son[x],fa); 47 for (int v,i=head[x];i;i=line[i].next){ 48 v=line[i].to; 49 if ((v!=f[x])&&(v!=son[x])) 50 dfs2(v,v); //轻儿子的top值为它本身 51 } 52 } 53 void pushdown(int root,int len){ 54 if (tree[root].mark){ 55 tree[root<<1].mark+=tree[root].mark; 56 tree[root<<1|1].mark+=tree[root].mark; 57 tree[root<<1].min+=tree[root].mark; 58 tree[root<<1|1].min+=tree[root].mark; 59 tree[root<<1].max+=tree[root].mark; 60 tree[root<<1|1].max+=tree[root].mark; 61 tree[root<<1].sum+=(long long)tree[root].mark*(long long)(len-(len>>1)); 62 tree[root<<1|1].sum+=(long long)tree[root].mark*(long long)(len>>1); 63 tree[root].mark=0; 64 } 65 } 66 void build(int root,int l,int r){ 67 tree[root].mark=0; 68 if (l==r){ 69 tree[root].min=val[dfn[l]]; 70 tree[root].max=val[dfn[l]]; 71 tree[root].sum=(long long)val[dfn[l]]; 72 return; 73 } 74 int mid=(l+r)>>1; 75 build(root<<1,l,mid); 76 build(root<<1|1,mid+1,r); 77 tree[root].min=min(tree[root<<1].min,tree[root<<1|1].min); 78 tree[root].max=max(tree[root<<1].max,tree[root<<1|1].max); 79 tree[root].sum=tree[root<<1].sum+tree[root<<1|1].sum; 80 } 81 long long get(int root,int l,int r,int x,int y){ 82 if ((x<=l)&&(y>=r)) return tree[root].sum; 83 long long ans=0; 84 pushdown(root,r-l+1); 85 int mid=(l+r)>>1; 86 if (x<=mid) ans=(get(root<<1,l,mid,x,y)+ans)%p; 87 if (y>mid) ans=(get(root<<1|1,mid+1,r,x,y)+ans)%p; 88 return ans; 89 } 90 void updata(int root,int l,int r,int x,int y,int z){ 91 if ((x<=l)&&(y>=r)){ 92 tree[root].min+=z; 93 tree[root].max+=z; 94 tree[root].sum+=(long long)z*(long long)(r-l+1); 95 tree[root].mark+=z; 96 return; 97 } 98 pushdown(root,r-l+1); 99 int mid=(l+r)>>1; 100 if (x<=mid) updata(root<<1,l,mid,x,y,z); 101 if (y>mid) updata(root<<1|1,mid+1,r,x,y,z); 102 tree[root].min=min(tree[root<<1].min,tree[root<<1|1].min); 103 tree[root].max=max(tree[root<<1].max,tree[root<<1|1].max); 104 tree[root].sum=tree[root<<1].sum+tree[root<<1|1].sum; 105 } 106 void change(int x,int y,int z){ 107 int f1=top[x],f2=top[y]; 108 while (f1!=f2){ 109 if (deep[f1]<deep[f2]){ 110 swap(f1,f2); 111 swap(x,y); 112 } 113 updata(1,1,t,id[f1],id[x],z); 114 x=f[f1]; 115 f1=top[x]; 116 } 117 if (x==y) {updata(1,1,t,id[y],id[x],z);return;} 118 if (deep[x]<deep[y]) swap(x,y); 119 updata(1,1,t,id[y],id[x],z); 120 } 121 long long sum(int x,int y){ 122 long long ans=0; 123 int f1=top[x],f2=top[y]; 124 while (f1!=f2){ 125 if (deep[f1]<deep[f2]){ 126 swap(f1,f2); 127 swap(x,y); 128 } 129 ans=(get(1,1,t,id[f1],id[x])+ans)%p; 130 x=f[f1]; 131 f1=top[x]; 132 } 133 if (x==y) return (ans+get(1,1,t,id[x],id[y])%p); 134 if (deep[x]<deep[y]) swap(x,y); 135 ans=(get(1,1,t,id[y],id[x])+ans)%p; 136 return ans; 137 } 138 int main(){ 139 scanf("%d%d%d%d",&n,&m,&r,&p); //r为根节点,p为取模 140 for (int i=1;i<=n;i++){ 141 scanf("%d",&val[i]); 142 deep[i]=0; 143 son[i]=-1; 144 } 145 for (int i=1,u,v;i<n;i++){ 146 scanf("%d%d",&u,&v); 147 add(u,v); 148 } 149 dfs1(r,r); 150 dfs2(r,r); 151 build(1,1,t); 152 while(m--){ //1为令b-c路径上的点权值+d,2为求b-c路径上点的权值和,3为令以b为根的子树的所有节点(包括自己)都+d,4为求以b为根节点的所有节点(包括自己)的权值和 153 scanf("%d",&a); 154 if (a==1){ 155 scanf("%d%d%d",&b,&c,&d); 156 change(b,c,d); 157 } 158 else if (a==2){ 159 scanf("%d%d",&b,&c); 160 printf("%lld\n",sum(b,c)%p); 161 } 162 else if (a==3){ 163 scanf("%d%d",&b,&c); 164 updata(1,1,t,id[b],id[b]+size[b]-1,c); 165 } 166 else if (a==4){ 167 scanf("%d",&b); 168 printf("%lld\n",get(1,1,t,id[b],id[b]+size[b]-1)%p); 169 } 170 } 171 return 0; 172 }
这里有个模板题可以去刷刷:https://www.luogu.org/problem/show?pid=3384
至于有边权值的树,我们可以将边权值存到该边所连的深度深的点上,这样在具体修改和询问操作中区间的定位id会有所不同,其他的都大同小异。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号