JZOJ.5279【NOIP2017模拟8.15】香港记者

Description

 

Input

Output

 

Sample Input

8 9
1 2 3 4 5 6 7 8
1 2 2
2 3 3
3 8 3
1 4 3
4 5 2
5 8 1
1 6 1
6 7 2
7 8 3

Sample Output

6
1 4 5 8）
 

Data Constraint

第一问就是最短路，可以考虑SPFA。

第二问问最短路中字典序（黑框眼镜数）最小的路径，我们可以考虑从终点搜向起点，用pre数组记录前驱，然后要更新距离的时候该点前驱必然要更新，距离相等时判断两条路径哪个字典序小就可以了。

（或者正向跑一边SPFA再反向跑一遍SPFA，那么就建出了关于起点和终点的最短路图，在这幅图上走既能保证一定是最短路，又能保证能走到终点，所以可以放心大胆地每步都走标号最小的）

 1 #include<iostream>
 2 #include<cstdio>
 3 #include<cstring>
 4 #include<cstdlib>
 5 #include<algorithm>
 6 #include<cmath>
 7 #include<ctime>
 8 #define N 200002
 9 using namespace std;
10 struct data{
11     int next,to;
12     long long power;
13 }line[N*2];
14 int team[N*2],head[N*2],visit[N],n,m,num,sign[N],pre[N],qwq[N],qaq,cnt;
15 long long dis[N];
16 void add(int v,int u,int w){
17     num++;
18     line[num].next=head[u];
19     line[num].to=v;
20     line[num].power=(long long)w;
21     head[u]=num;
22 }
23 bool QAQ(int p,int n){
24     int x=p,y=n;
25     while (sign[x]==sign[y]&&x!=0&&y!=0){
26         x=pre[x];
27         y=pre[y];
28     }
29     if (sign[x]<sign[y]) return false;
30     return true;
31 }
32 void SPFA(){
33     pre[n]=0;
34     int l=0,r=1,v=0,u=0;
35     memset(visit,false,sizeof(visit));
36     memset(dis,127,sizeof(dis));
37     team[r]=n;
38     dis[n]=0;
39     visit[n]=true;
40     while (l<r){
41         u=team[++l];
42         for (int i=head[u];i;i=line[i].next){
43             v=line[i].to;
44             if (dis[u]+line[i].power<dis[v]){
45                 if (!visit[v]){
46                     visit[v]=true;
47                     team[++r]=v;
48                 }
49                 pre[v]=u;
50                 dis[v]=dis[u]+line[i].power;
51             }
52             else if (dis[u]+line[i].power==dis[v])
53              if (QAQ(pre[v],u)) pre[v]=u;
54         }
55         visit[u]=false;
56     }
57 }
58 int main(){
59     scanf("%d%d",&n,&m);
60     for (int i=1;i<=n;i++)
61      scanf("%d",&sign[i]);
62     num=0;
63     for (int i=1,u,v,w;i<=m;i++){
64         scanf("%d%d%d",&u,&v,&w);
65         add(u,v,w);
66     }
67     SPFA();
68     qaq=1;
69     cnt=0;
70     while(qaq!=0){
71      qwq[++cnt]=sign[qaq];
72      qaq=pre[qaq];
73     }
74     printf("%lld\n",dis[1]);
75     for (int i=1;i<=cnt;i++)
76      printf("%d ",qwq[i]);
77     return 0;
78 }
神奇的代码

其实我们倒着搜遇到距离相等时可以直接比较前驱点的黑框数和当前点的黑框数，直接改，虽然存在反例（如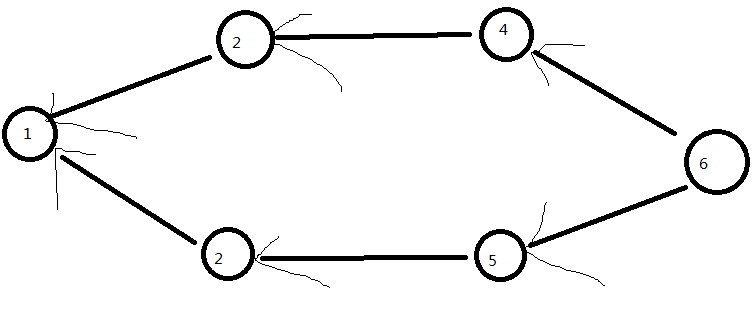这个已经反向建边，且点内为黑框眼镜个数，两条路的长度假设相等，这样程序就可能会得出1 2 5 6，这要看读入边的顺序233，不过数据太水没有这情况）

前60%的数据随机这告诉我们最短路很有可能只有一条

posted @ 2017-08-15 22:40  ~Lanly~  阅读(235)  评论(0)  编辑  收藏  举报