JZOJ.5236【NOIP2017模拟8.7】利普希茨

Description

 

Input

输入文件名为lipschitz.in。
第一行一个整数n。
接下来一行n个整数，描述序列A。
第三行一个数q 。
接下来q行，每行三个整数。其中第一个整数type表示操作的类型。 type=0对应修改操作， type=1对应查询操作。

Output

输出文件名为lipschitz.out。
对于每个查询，给出f(A[l..r]) 。
 

Sample Input

输入1：
6
90 50 78 0 96 20
6
0 1 35
1 1 4
0 1 67
0 4 11
0 3 96
1 3 5

输入2：
50
544 944 200 704 400 150 8 964 666 596 850 608 452 103 988 760 370 723 350 862 856 0 724 544 668 891 575 448 16 613 952 745 990 459 740 960 752 194 335 575 525 12 618 80 618 224 240 600 562 283
10
1 6 6
1 1 3
0 11 78279
0 33 42738
0 45 67270
1 1 26
1 19 24
1 37 39
1 8 13
0 7 64428

Sample Output

输出1：
78
85

输出2：
0
744
77683
856
558
77683
 

Data Constraint

对于30%的数据，n,q<=500
对于60%的数据，n,q<=5000
对于100%的数据，n,q<=100000,0<=ai,val<=10^9

 这里有一个结论：f(A)的最大值是相邻的两点的差值。

我们可以设想一下，一个区间被里面min和max分成了三段，其中i=min,j=max，那么设对应的f(A)的值为a,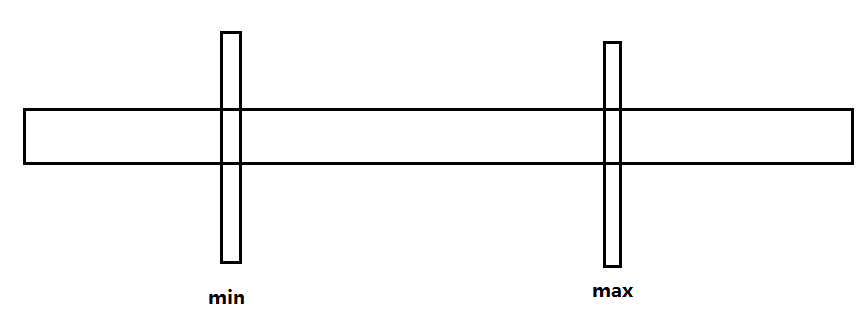

那么我们可以枚举里面的左端点i右端点j来计算f(A)的值与a比较

首先很肯定的一点 区间[i,j]不能跨过min和max，那么我们会对这三段区间不断细分，到最后也就只剩下相邻的两个点了，此时就是最大值和最小值（这个似乎不能证明）

 

还有个几何证明：f(A)可以看成一个斜率的绝对值，那么对于坐标上的三个点a,b,c来说，它们三点确定的直线中，很显然横坐标越靠近的两个点斜率会越大

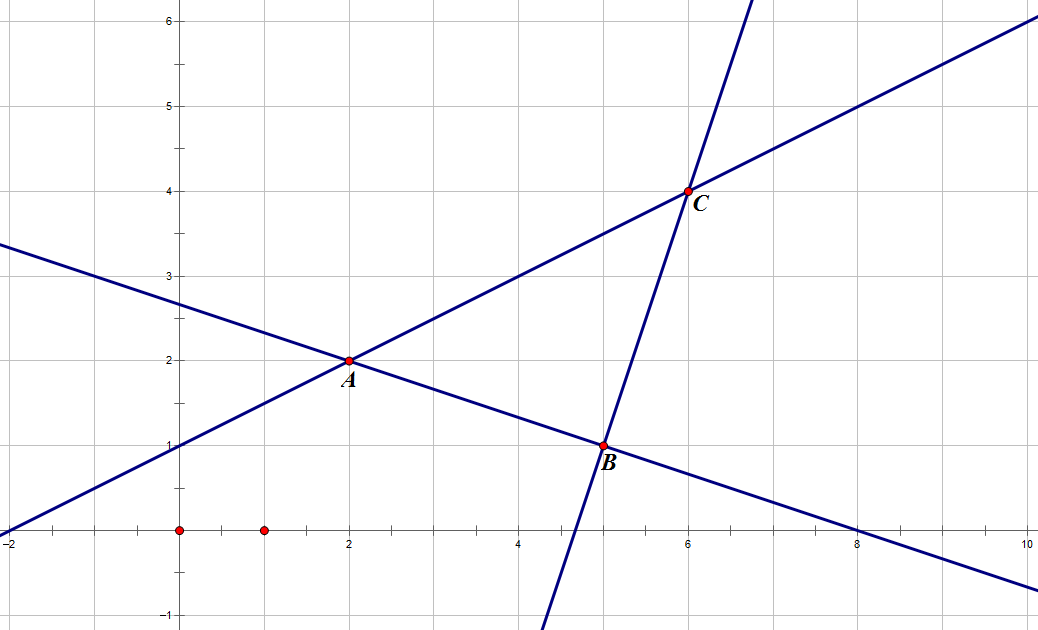
（转自mcw的证明）令$\Delta_i=A_{i+1}-A_i$,则$\left\lceil\frac{|A_j-A_i|}{j-i}\right\rceil=\left\lceil\frac{|\sum_{k=i}^{j-1}\Delta_k|}{j-i}\right\rceil=\overline{\Delta_{i\,..\,j-1}}$，显然会有$\Delta_i\,..\,\Delta_{j-1}$中的一项大于等于$\overline{\Delta_{i\,..\,j-1}}$

所以这题就变成了维护差值的修改和最值了，线段树就可以了。

 1 #include<iostream>
 2 #include<cstdio>
 3 #include<cstring>
 4 #include<algorithm>
 5 #include<cstdlib>
 6 #include<cmath>
 7 using namespace std;
 8 int maxx[4000000],n,q,a[1000002],x,l,r,d[1000002];
 9 void buildtree(int root,int l,int r){
10     if (l==r) {maxx[root]=d[l]; return;}
11     int mid=(l+r)>>1;
12     buildtree(root<<1,l,mid);
13     buildtree(root<<1|1,mid+1,r);
14     maxx[root]=max(abs(maxx[root<<1]),abs(maxx[root<<1|1]));
15 }
16 void change(int root,int l,int r,int x,int c){
17     if (l==r){
18         maxx[root]+=c;
19         return;
20     }
21     int mid=(l+r)>>1;
22     if (x<=mid) change(root<<1,l,mid,x,c);
23     if (x>mid) change(root<<1|1,mid+1,r,x,c);
24     maxx[root]=max(abs(maxx[root<<1]),abs(maxx[root<<1|1]));    
25 }
26 int get(int root,int l,int r,int x,int y){
27     if ((x<=l)&&(y>=r)) return abs(maxx[root]);
28     int ans=0;
29     int mid=(l+r)>>1;
30     if (x<=mid) ans=max(ans,get(root<<1,l,mid,x,y));
31     if (y>mid) ans=max(ans,get(root<<1|1,mid+1,r,x,y));
32     return ans;
33 }
34 int main(){
35     freopen("lipschitz.in","r",stdin);
36     freopen("lipschitz.out","w",stdout);
37     scanf("%d",&n);
38     for (int i=1;i<=n;i++){
39      scanf("%d",&a[i]);
40      d[i]=a[i]-a[i-1];
41     }
42     buildtree(1,1,n);
43     scanf("%d",&q);
44     while (q--){
45      scanf("%d%d%d",&x,&l,&r);
46      if (x==0)  {change(1,1,n,l,r-a[l]);change(1,1,n,l+1,-r+a[l]); a[l]=r;}
47      if (x==1)  printf("%d\n",get(1,1,n,l+1,r));
48  }
49     return 0;
50 }
神奇的代码

数学很重要

posted @ 2017-08-07 22:04  ~Lanly~  阅读(219)  评论(0)  编辑  收藏  举报