二分图匹配之最大匹配——匈牙利算法
今天也开始学习了下二分图匹配
二分图匹配是网络流最大流的一种特殊情况。
二分图形式类似于下图
点分为了左右两部分，两部分之间的点有若干条线段相连，但在左部分或右部分之间的点没有线段相连。
好比左边三位男员工，右边三位女员工，连线代表着他们之间互有好感233但现在我们需要一男一女一起搭配干活（不累嘛~）于是乎问题来了，最大能搭配几对互有好感的男女一起去干活。
解决此类 二分图匹配 的问题，用到的是叫匈牙利算法。
在介绍着算法之前，我们知道二分图匹配是特殊的最大流问题，也就是说套最大流的模板也能解出来，只要将原图改成如下即可：
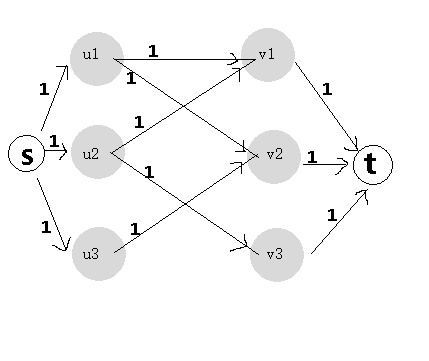
将原图中的所有无向边 e 改为有向边，方向从U到V，容量为1，增加源点 s 和汇点 t ，从s向所有的顶点u∈U连一条容量为1的边，从所有的顶点v∈V 向 t 连一条容量为1的边。
Dinic算法是不断地寻找增广路然后不断增广，直到不存在增广路停止。
在这个算法里面，我们人为地规定了反向弧，能够隐蔽地让计算机对之前错误的选择更改，再加上这里的容量是1，在此，匈牙利算法便是明显地遇错就改。
它的思路是：
1.从第一个元素开始进行匹配。
2.遇到左边某个元素u所要匹配的右边另一个元素v，但v先前已经被匹配了，于是就尝试地更改先前和m匹配的左边元素x，如果能够改变，就让u与v元素匹配，而之前的x就和右边另一个能匹配元素（有连线的）匹配了233（这里可以运用递归）
3.如果不能更改，便放弃该元素。
4.重复步骤2，直到最后一个元素。此时的匹配数即为最大。
换句话就是说 有机会就匹配，没机会创造机会去匹配。
时间复杂度：
左边的点的个数n*总边数m；
O(nm)。
1 bool find(int u){ //u为当前正在匹配的左边元素 2 for (int v=1;v<=m;v++){ //扫描右边每个元素v 3 if (line[u][v]==true && used[v]==false) 4 // line[u][v]==true表示元素u和v之间有连线，used[v]表示这个元素的曾是否有过要更改匹配的，这样可以省下一些时间 5 { 6 used[v]=1; 7 if (f[v]==0 || find(f[v])) { //f[v]表示v元素所匹配的元素 8 //f[v]==0表示该元素仍未匹配 find(f[v])是去尝试能否改变匹配j元素的元素的匹配（就是先前匹配j的元素x能否匹配另一个元素） 9 f[v]=u; 10 return true; 11 } 12 } 13 } 14 return false; 15 } 16 17 匈牙利算法
主程序里
1 for (i=1;i<=n;i++) //依次对左边每个元素进行匹配 2 { 3 memset(used,0,sizeof(used)); //每一步中清空 4 if find(i) ans+=1; 5 }
