📂Codeforces

🔖DP 博弈论构造期望DP 思维

2023-04-29 13:39阅读: 168评论: 0推荐: 2

Codeforces Round 868 Div 2

A. A-characteristic (CF 1823 A)

题目大意

要求构造一个仅包含 $1$ 和 $-1$ 的长度为 $n$ 的数组 $a$ ，使得存在 $k$ 个下标对 $(i, j), i < j$ 满足 $a_i \times a_j = 1$ 。

解题思路

当有 $x$ 个 $1$ ， $y$ 个 $-1$ 时，其满足条件的下标对数量为 $\frac{x (x - 1)}{2} + \frac{y (y - 1)}{2}$ 。

由于 $n$ 只有 $100$ ，直接枚举 $x$ 即可。

神奇的代码

 #include <bits/stdc++.h>
using namespace std;
using LL = long long;
 
int main(void) {
    ios::sync_with_stdio(false); 
    cin.tie(0); cout.tie(0);
    int t;
    cin >> t;
    while(t--){
        int n, k;
        cin >> n >> k;
        int one = 0;
        for(; one <= n; ++ one){
            int neg = n - one;
            if (neg * (neg - 1) + one * (one - 1) == 2 * k)
                break;
        }
        if (one > n)
            cout << "No" << '\n';
        else{
            cout << "Yes" << '\n';
            for(int i = 0; i < one; ++ i)
                cout << 1 << ' ';
            for(int i = 0; i < n - one; ++ i)
                cout << -1 << ' ';
            cout << '\n';
        }
    }
 
    return 0;
}

B. Sort with Step (CF 1823 B)

题目大意

给定一个排序，问能否仅通过交换相隔 $k$ 的俩元素，使得有序。不能的话问能否事先通过一次任意交换操作后，再通过之前的操作交换得到有序。

解题思路

考虑每个元素的原始位置和最后所在的位置，它们对 $k$ 的取模应该相同。否则就不能有序。

而如果恰好有两个元素其对 $k$ 的取模不同，且交换之后是相同的，则可以。

神奇的代码

 #include <bits/stdc++.h>
using namespace std;
using LL = long long;
 
int main(void) {
    ios::sync_with_stdio(false); 
    cin.tie(0); cout.tie(0);
    int t;
    cin >> t;
    while(t--){
        int n, k;
        cin >> n >> k;
        vector<int> a(n);
        for(auto &i : a){
            cin >> i;
            i --;
        }
        bool ok1 = true;
        map<pair<int, int>, int> cnt;
        for(int i = 0; i < n; ++ i){
            if (i % k != a[i] % k){
                ok1 = false;
                cnt[{min(i % k, a[i] % k), max(i % k, a[i] % k)}] ++;
            }
        }
        if (ok1)
            cout << 0 << '\n';
        else if (cnt.size() == 1 && cnt.begin()->second == 2)
            cout << 1 << '\n';
        else 
            cout << -1 << '\n';
    }
 
    return 0;
}

C. Strongly Composite (CF 1823 C)

题目大意

给定一个数组 $a$ ，构造数组 $b$ ，要求最大化数组的元素数量，使得俩数组的所有元素的乘积相同，且数组 $b$ 的每个数都是强合数。

强合数的定义为，合数因子数量 $\geq$ 质数因子数量。

解题思路

乘积相同，相当于将数组 $a$ 里的质数重新组合；数量最大，相当于尽可能少用质数来组成一个新的数。

可以发现，两个相同的质数组成一个强合数，或者三个不同的质数可以组成一个强合数。

由此我们统计数组 $a$ 中的每个质数的数量，同个质数俩俩组合，不同质数三三组合，就能最大化答案了。

神奇的代码

 #include <bits/stdc++.h>
using namespace std;
using LL = long long;
 
int main(void) {
    ios::sync_with_stdio(false); 
    cin.tie(0); cout.tie(0);
    int t;
    cin >> t;
    while(t--){
        int n;
        cin >> n;
        map<int, int> cnt;
        auto fac = [&](int a){
            for(int i = 2; i * i <= a; ++ i){
                while (a % i == 0){
                    cnt[i] ++;
                    a /= i;
                }
            }
            if (a != 1)
                cnt[a] ++;
        };
        for(int i = 0; i < n; ++ i){
            int a;
            cin >> a;
            fac(a);
        }
        LL ans = 0;
        int left = 0;
        for(auto &[_, value] : cnt){
            ans += value / 2;
            left += (value & 1);
        }
        ans += left / 3;
        cout << ans << '\n';
 
    }
 
    return 0;
}

D. Unique Palindromes (CF 1823 D)

题目大意

要求构造一个仅包含小些字母的字符串 $s$ ，长度为 $n$ ，且满足 $k$ 个限制。

每个限制表述为 $(x_i, c_i)$ ，字符串 $s$ 的长度为 $x_i$ 的前缀满足有 $c_i$ 个本质不同的回文串）

解题思路

通过打表发现本质不同的回文串数量不会超过字符串长度。

注意到 $k$ 最大只有 $20$ ，这启示我们每个限制可以用一个字符去满足。

思考朴素的构造方法，对于一个长度为 $n$ 的字符串，我们可以 $aaaaaaaabcabcabc$ 这样去构造，一开始连续的 $a$ 的数量就能控制这个字符串的本质不同的回文串的数量。这样的构造方法满足其数量在 $[3, n]$ 之内，这刚好符合题意里 $c_i \geq 3$ 的限制。

因此我们可以先根据第一个限制构造出如上的字符串，对于之后的限制进行增量构造，增加的回文数量用 $dddd$ ， $eeeee$ 这样构造，剩下的长度用 $abc$ 这样不会增加回文串数量的形式去填充。

注意用于填充的字符串，在每次填充时应该继续前面的，而不是从头（从 $abc$ ）开始（如代码的fill_cur），不然可能会新增回文串。

神奇的代码

 #include <bits/stdc++.h>
using namespace std;
using LL = long long;
 
int main(void) {
    ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);
    int t;
    cin >> t;
    while(t--){
        int n, k;
        cin >> n >> k;
        vector<int> x(k), c(k);
        for(auto &i : x)
            cin >> i;
        for(auto &i : c)
            cin >> i;
        string ans;
        int fill_cur = 0;
        auto fill = [&](int x){
            while(x--){
                ans.push_back('a' + fill_cur);
                fill_cur = (fill_cur + 1) % 3;
            }
        };
        auto ok = [&](){
            int cur = 0;
            for(int i = 0; i < k; ++ i){
                int dis = x[i] - c[i];
                if (dis < 0)
                    return false;
                if (cur > dis)
                    return false;
                cur = dis;
            }
 
            ans += string(c[0] - 3, 'a');
            fill(x[0] - ans.size());
            for(int i = 1; i < k; ++ i){
                ans += string(c[i] - c[i - 1], 'c' + i);
                fill(x[i] - ans.size());
            }
            return true;
        };
        if (ok()){
            cout << "YES" << '\n';
            cout << ans << '\n';
        }else {
            cout << "NO" << '\n';
        }
    }
 
    return 0;
}

E. Removing Graph (CF 1823 E)

题目大意

两人博弈。

给定 $n$ 个环，每个人可以从 $[l, r]$ 中选一个数 $x$ ，然后选择由 $x$ 个点组成的连通子图，将点及其边去掉。不能操作者输。

在绝顶聪明的情况下，问先后手谁必赢。

解题思路

每个环都是一个独立局面，因此我们求出每个环的 $sg$ 值，异或起来，非零就先手赢，否则后手赢。

对于一个环来说，取了一次之后就变成一条链了。因此一个环的 $sg$ 值就是所有可能的链的长度对应的 $sg$ 值的 $mex$ 。

对于一个链来说，取了一次之后就变成两条链，这两条链分别都是一个独立局面，因此一个链的 $sg$ 值，就是一些操作值的 $mex$ ，而操作值就是取了之后（有取的长度和取的位置两个因素）的两个链的 $sg$ 值的异或。

abc287g和abc297g就是要求一个链的 $sg$ 值。

注意到题目保证了 $l \neq r$ ，对于一条链来说，如果它能取（即长度 $\geq l$ ），则必定能分成两条长度一样的链，之后先手就模仿后手的操作，就能必赢了。

也就是说，对于一个环来说，如果其长度 $len \geq l + r$ ，那么先手取了一次后，变成的链因为后手必定可以再取（ $len - r \geq l$ )，所以对于后手来说必定是个必胜态，所以这样的环对于先手来说必定是个必败态，其 $sg$ 值为 $0$ 。

而长度小于 $l$ ，不能取，那肯定是必败态，其 $sg$ 值为 $0$ 。

考虑环长度在 $[l, l+r)$ 之间的 $sg$ 值，其对应的链长度有 $len - l, len - l - 1, len - l - 2, ..., len - r$ 。其 $sg$ 值就是这些可能的链长度的 $sg$ 值取 $mex$ 。

考虑链长度，小于 $l$ ，是必败态，其 $sg$ 值为 $0$ 。而 $sg(l) = sg(l + 1) = sg(l + 2) ... = sg(l + l - 1) = 1$ ，

$sg(2l) = mex(sg(l), sg(l - 1), sg(l - 2), ..., sg(1), sg(0)) = mex(1, 0, 0, 0, ..., 0) = 2 = sg(2l + 1) = sg(2l + 2)$

$sg(3l) = mex(sg(2l), sg(2l - 1), ..., sg(l), sg(l - 1), ..., sg(0)) = mex(2, 1, ..., 1, 0, ..., 0) = 3 = sg(3l + 1) = sg(3l + 2)$

上述的 $mex$ 里的每一项都是取最边边的结果（即取了之后还有一个链），至于有两条链的结果，是长度更小的两个链的 $sg$ 的异或值，其不会超过上面的最大值。

由此（或打表）可以发现长度为 $sg(len) = \lfloor \frac{len}{l} \rfloor(l \leq len < l + r)$

进而环的 $sg_c(len) = mex(sg(len - l), sg(len - l - 1), ..., sg(len - r)) = \lfloor \frac{len}{l} \rfloor(l \leq len < l + r)$

环的 $sg$ 值求出来了，异或一下就知道谁赢了。

至于环大小，用并查集或 $BFS$ 一下就知道了。

神奇的代码

 #include <bits/stdc++.h>
using namespace std;
using LL = long long;
 
class dsu {
    public:
    vector<int> p;
    vector<int> sz;
    int n;
 
    dsu(int _n) : n(_n) {
        p.resize(n);
        sz.resize(n);
        iota(p.begin(), p.end(), 0);
        fill(sz.begin(), sz.end(), 1);
    }
 
    inline int get(int x) {
        return (x == p[x] ? x : (p[x] = get(p[x])));
    }
 
    inline bool unite(int x, int y) {
        x = get(x);
        y = get(y);
        if (x != y) {
            p[x] = y;
            sz[y] += sz[x];
            return true;
        }
        return false;
    }
};
 
int main(void) {
    ios::sync_with_stdio(false); 
    cin.tie(0); cout.tie(0);
    int n, l, r;
    cin >> n >> l >> r;
    dsu d(n);
    for(int i = 0; i < n; ++ i){
        int u, v;
        cin >> u >> v;
        -- u;
        -- v;
        d.unite(u, v);
    }
    int ans = 0;
    for(int i = 0; i < n; ++ i){
        if (d.get(i) == i){
            if (d.sz[i] >= l && d.sz[i] < l + r)
                ans ^= d.sz[i] / l;
        }
    }
    if (ans)
        cout << "Alice" << '\n';
    else 
        cout << "Bob" << '\n';
 
    
 
    return 0;
}

F. Random Walk (CF 1823 F)

题目大意

树上随机游走，从点 $s$ 到点 $t$ ，问每个点访问次数的期望值。

解题思路

每次的期望题感觉都比较神仙。

注意到这是棵树，点 $s$ 到点 $t$ 的路径是唯一的，设路径为 $s, u_0, u_1, ..., u_k, t$ 。

一开始设状态 $dp[s][v][t]$ 表示从 $s$ 点到 $t$ 点，期望访问到 $v$ 号点的次数，然后枚举到相邻点的状态，即 $dp[s][v][t] = \sum_{(s, u) \in E}dp[u][v][t]$ ，但感觉怎么都算不出来。

然后想着从点 $s$ 出发，它可以往很多个相邻点走，只有一个点 $u_0$ 是更接近点 $t$ 的，且最终到点 $t$ 时立刻停下来，这意味着点 $t$ 之后的点的访问次数的期望值一定是 $0$ 。

考虑到一旦走到点 $u_0$ 时，发现问题貌似变成了一个子问题了，可以认为是从点 $u_0$ 出发，到点 $t$ 的情况。换句话说，我们可以将点 $s$ 到点 $t$ 的步骤分成若干步，分别是点 $s$ 到点 $u_0$ ，点 $u_0$ 到点 $u_1$ ... 点 $u_t$ 到点 $t$ ，由于期望的线性可加性，每个点的期望访问次数，可以由这些的每个步骤的影响依次累计。

设 $dp[s][w]$ 表示从 $s$ 点往更接近点 $t$ 的方向走（即走到 $u_0$ 点），对 $w$ 点的期望访问次数。

设点 $s$ 的度数为 $du_s$ ，其余字母定义看图，根据期望定义，可以得到：

tree

d p [s] [w] = \frac{1}{d u_{s}} \times 0 + \frac{1}{d u_{s}} (d p [x] [w] + d p [s] [w]) + \frac{d u_{s} - 2}{d u_{s}} (d p [y] [w] + d p [s] [w])

$dp[s][w] = \frac{1}{du_s} \times 0 + \frac{1}{du_s} (dp[x][w] + dp[s][w]) + \frac{du_s - 2}{du_s}(dp[y][w] + dp[s][w])$

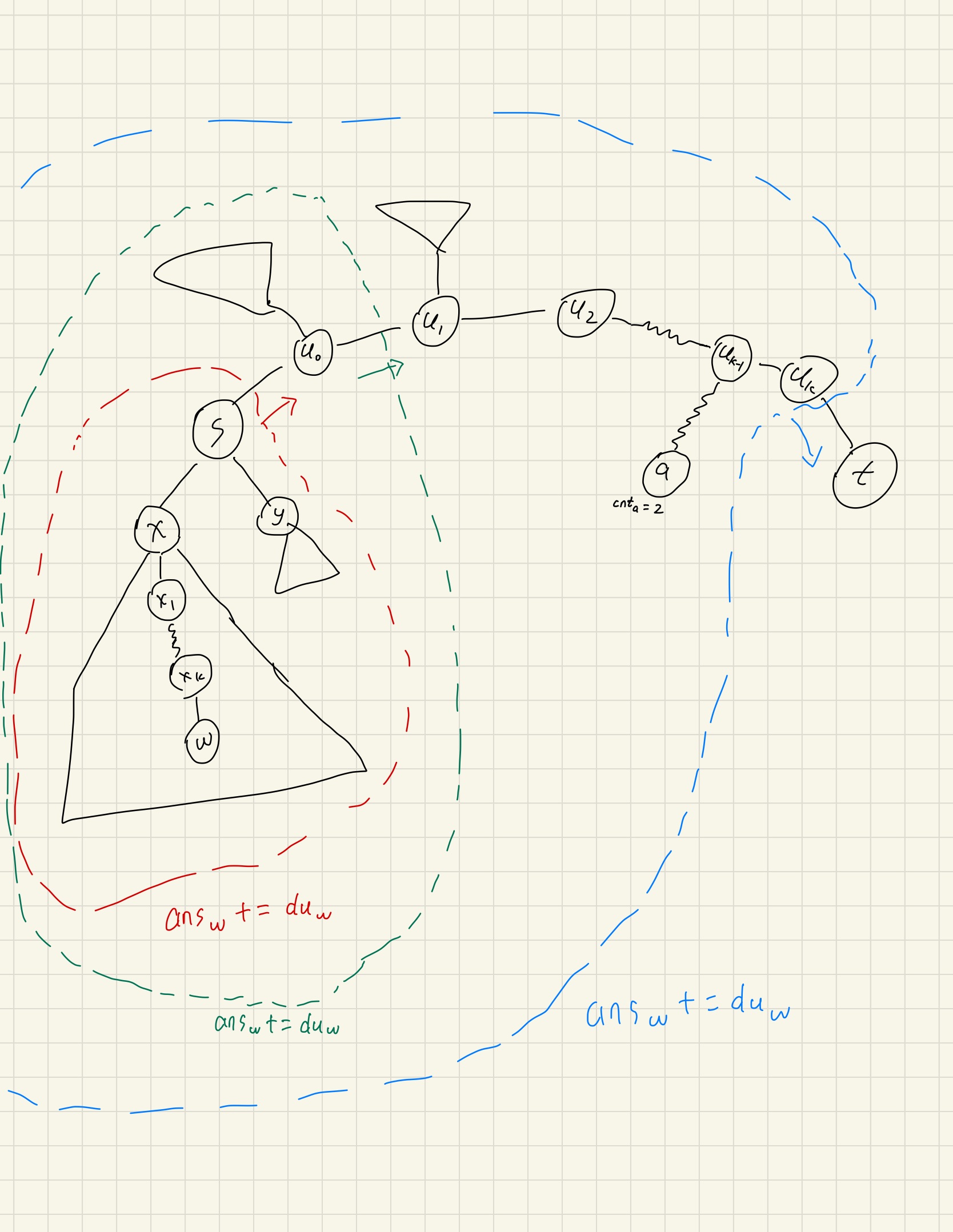
这里有三个部分：

有 $\frac{1}{du_s}$ 的概率选择走到 $u_0$ ，然后就停下来了，此时对 $v$ 的访问贡献是 $0$ 。
有 $\frac{1}{du_s}$ 的概率往 $w$ 所在的子树走（即点 $x$ ），此时对 $w$ 的访问贡献是由 $x \to s$ 和 $s \to u_0$ 组成，即 $dp[x][w] + dp[s][w]$ 。
有 $\frac{du_s - 2}{du_s}$ 的概率往其他子树走（即点 $y$ 表示的其他所有点），此时对 $w$ 的访问贡献是由 $y \to s$ 和 $s \to u_0$ 组成，即 $dp[y][w] + dp[s][w]$ 。但由于从点 $y$ 到点 $w$ 必须经过点 $s$ ，而一旦到点 $s$ 就会停下来（ $dp[y][w]$ 即表示从点 $y$ 到更接近点 $t$ 的方向走（即往点 $s$ ），对点 $w$ 的访问贡献），因此 $dp[y][w] = 0$ 。

这样上述式子移一下项，就得到

d p [s] [w] = d p [x] [w]

$dp[s][w] = dp[x][w]$

即点 $s$ 往点 $u_0$ 走时的对点 $w$ 访问次数的贡献是等价于点 $x$ 往点 $s$ 走时，对点 $w$ 的贡献。由此就可以得到

d p [s] [w] = d p [x] [w] = d p [x_{1}] [w] = . . . = d p [x_{k}] [w] = d p [w] [w]

$dp[s][w] = dp[x][w] = dp[x_1][w] = ... = dp[x_k][w] = dp[w][w]$

剩下的就是求 $dp[w][w]$ 。根据期望定义，可以得到

d p [s] [s] = \frac{1}{d u_{s}} \times 1 + \frac{d u_{s} - 1}{d u_{s}} (d p [o] [s] + d p [s] [s])

$dp[s][s] = \frac{1}{du_s} \times 1 + \frac{du_s - 1}{du_s}(dp[o][s] + dp[s][s])$

这里有两部分：

有 $\frac{1}{du_s}$ 的概率选择走到 $u_0$ ，此时就停下来了，因此对 $s$ 的访问贡献是 $1$ （一开始在 $s$ 时的贡献）。
有 $\frac{du_s - 1}{du_s}$ 的概率选择走到除点 $u_0$ 之外的其他点(设点 $o$ ，即 $x$ 或 $y$ )，因此对 $s$ 的访问贡献是 $o \to s$ 和 $s \to s$ ，即 $dp[o][s] + dp[s][s]$ ，而因为点 $o$ 到点 $s$ 就会停下来（点 $s$ 是更接近点 $t$ 的点），因此 $dp[o][s] = 1$ （一开始在 $s$ 时的贡献包含在 $dp[s][s]$ 里）。

这样上述式子移一下项，就得到

d p [s] [s] = d u_{s}

$dp[s][s] = du_s$

综合上述的两个式子 $dp[s][w] = dp[w][w] = du_w$ ，可以得出，每当进行一次 $s \to u_0, u_0 \to u_1,\cdots, u_k \to t$ 时，其他点 $w$ 的期望访问次数都会增加 $du_w$ ，其中点 $w$ 是点 $s$ 除了 $u_0$ 方向的其他方向的点（见上图的虚线包括起来，就是对应颜色的箭头的影响）。

也就是说一个点 $a$ 的期望访问次数就是 $du_a \times cnt_a$ ，其中 $cnt_a$ 等于该点与路径 $s \to t$ 的交点（以上图为例，就为 $u_{k-1}$ ）到 $t$ 的点数（见上图的点 $a$ ）。

剩下的就是如何求 $cnt_w$ ，我们可以以点 $s$ 为根，然后我们从点 $t$ 开始，一路沿着父亲节点上去，就回到点 $s$ ，其中每往父亲跳一次时， $cnt_w$ 就会加一，比如从 $t \to u_k$ 时， $cnt = 0 + 1 = 1$ ，此时再遍历一下除了 $t$ 和 $u_{k - 1}$ 方向的所有点 $w$ ，它们的答案就是 $du_w \times cnt$ 。

最终的时间复杂度是 $O(n)$ 。

虽然答案不会超过 $n^2$ ，但记得对 $998244353$ 取模。

神奇的代码

 #include <bits/stdc++.h>
using namespace std;
using LL = long long;
 
const int mod = 998244353;
 
int main(void) {
    ios::sync_with_stdio(false); 
    cin.tie(0); cout.tie(0);
    int n, s, t;
    cin >> n >> s >> t;
    -- s, -- t;
    vector<vector<int>> edge(n);
    vector<int> du(n);
    for(int i = 1; i < n; ++ i){
        int u, v;
        cin >> u >> v;
        -- u, -- v;
        edge[u].push_back(v);
        edge[v].push_back(u);
        ++ du[u];
        ++ du[v];
    }
    vector<int> fa(n);
    function<void(int, int)> dfs = [&](int u, int f){
        fa[u] = f;
        for(auto &v : edge[u]){
            if (v == f)
                continue;
            dfs(v, u);
        }
    };
    dfs(s, s);
    vector<int> ans(n);
    int cnt = 1;
    ans[t] = 1;
    function<void(int, int, int)> dfs2 = [&](int u, int f, int cnt){
        ans[u] = 1ll * du[u] * cnt % mod;
        for(auto &v : edge[u]){
            if (v == f)
                continue;
            dfs2(v, u, cnt);
        }
    };
    do{
        int cur = fa[t];
        ans[cur] = 1ll * cnt * du[cur] % mod;
        for(auto &u : edge[cur]){
            if (u != fa[cur] && u != t)
                dfs2(u, cur, cnt);
        }
        t = cur;
        ++ cnt;
    }while(s != t);
    for(auto &i : ans)
        cout << i << ' ';
    cout << '\n';
 
    return 0;
}

本文作者：~Lanly~

本文链接：https://www.cnblogs.com/Lanly/p/17363927.html

posted @ 2023-04-29 13:39 ~Lanly~ 阅读(168) 评论(0) 编辑收藏举报

刷新页面返回顶部

登录后才能查看或发表评论，立即登录或者逛逛博客园首页

公告

昵称：~Lanly~ 园龄：8年3个月粉丝：301 关注：55

昵称： ~Lanly~
园龄： 8年3个月
粉丝： 301
关注： 55

+加关注

指尖跃动的换行符，是我此生不变的信仰。|

2025年3月

日

一

二

三

四

五

六

~Lanly~

指尖跃动的换行符，是我此生不变的信仰。

Codeforces Round 868 Div 2

A. A-characteristic (CF 1823 A)

题目大意

解题思路

B. Sort with Step (CF 1823 B)

题目大意

解题思路

C. Strongly Composite (CF 1823 C)

题目大意

解题思路

D. Unique Palindromes (CF 1823 D)

题目大意

解题思路

E. Removing Graph (CF 1823 E)

题目大意

解题思路

F. Random Walk (CF 1823 F)

题目大意

解题思路

公告

我的标签

随笔分类

随笔档案

友情链接

阅读排行榜

评论排行榜

推荐排行榜

最新评论

	#include <bits/stdc++.h>
	using namespace std;
	using LL = long long;

	int main(void) {
	ios::sync_with_stdio(false);
	cin.tie(0); cout.tie(0);
	int t;
	cin >> t;
	while(t--){
	int n, k;
	cin >> n >> k;
	int one = 0;
	for(; one <= n; ++ one){
	int neg = n - one;
	if (neg * (neg - 1) + one * (one - 1) == 2 * k)
	break;
	}
	if (one > n)
	cout << "No" << '\n';
	else{
	cout << "Yes" << '\n';
	for(int i = 0; i < one; ++ i)
	cout << 1 << ' ';
	for(int i = 0; i < n - one; ++ i)
	cout << -1 << ' ';
	cout << '\n';
	}
	}

	return 0;
	}