单向链表

线性表的链式存储结构

线性表中每个节点有唯一的前趋节点和后趋节点

设计链式存储结构时，不要求逻辑上相邻的两个元素在物理上也相邻，数据元素之间的逻辑关系通过指针建立。这样的数据结构我们称之为链表。

分类	特点
单向链表	每个物理节点增加一个指向后继节点的指针
双向链表	在单链表的基础上再给每一个节点增加一个指向前趋节点的指针

本文重点介绍单链表

C语言课程中曾简要地介绍过链表这种数据结构，当时并没有强调这个头节点的重要性。现在我们来分析一下带头节点链表的优点

1. 第一个节点的操作和表中其他节点的操作相一致，无需特殊处理。
2. 无论链表是否为空，都有一个头节点，统一了空表和非空表的处理。

如果不设置头节点，需要特殊处理第一个节点
<\n>
建表：第一个元素写入到表头指针指向的位置，设置计数器cnt记录结点数，当cnt = 0的写入表头，cnt > 0时写入到其他位置。
<\n>
删除节点：删除第一个元素时需另外设置一个指针变量存储第二个结点的地址，完成操作之后让表头指针指向第二个结点。

链表的存储密度

存储密度是指节点数据本身所占的存储量和整个节点结构中所占的存储之比，即
$$存储密度=\frac{节点数据本身占用的空间}{节点占用的空间总量}$$

例如：

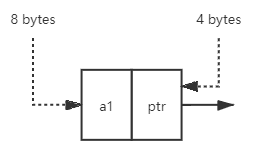
$$存储密度=\frac{8}{8+4}=0.67$$

需要特别指出的是：结构体的大小不是成员变量大小的简单加和
具体原理涉及到计算机组成原理中的边界对齐问题，在数据结构部分不详细展开，有兴趣的小伙伴可以在文末拓展阅读部分进一步学习

一般地，存储密度越大，存储空间的利用率就越高。
顺序表的存储密度为1，因为顺序表是连续的，不需要指针连接；
而链表的存储密度就小于1。

节点

用Elemtype泛指数据元素的类型

typedef struct _node{
	Elemtype data;
	struct _node *next;
}linkList;

typedef后面的_node是必要的，目的是让节点内的指针知道，自己应该指向_node这种类型的东西。

成员	介绍
data	数据域，用于存储线性表的一个数据元素
next	指针域，用于存放一个指针，该指针指向本结点的后继结点

当next为NULL，它不指向任何结点，起标志链表结尾的作用

建立单向链表的两种方法

头插法

1. 从一个空表开始，创建一个头节点
2. 依次读取数组a中的元素，生成新节点
3. 将新节点插入到当前链表的表头上，直到结束为止

void
createList1( linkList **l, int a[], int n )
{
	linkList *s;
	int i;
	( *l ) = ( linkList* )malloc( sizeof( linkList ) );
	( *l )->next = NULL;
	for( i = 0; i < n; i++ ){
		s = ( linkList* )malloc( sizeof( linkList ) );
		s->data = a[i];
		s->next = ( *l )->next;
		( *l )->next = s;
	}
}

尾插法

1. 从一个空表开始，创建一个头节点
2. 依次读取数组a中的元素，生成新节点
3. 将新节点插入到当前链表的表尾上，直到结束为止

增加一个尾指针tail，使其始终指向当前链表的尾节点，采用尾插法建表，链表的节点顺序与逻辑次序相同

void
createList2( linkList **l, int a[], int n )
{
	int i;
	linkList *cur, *tail;
	( *l ) = ( linkList* )malloc( sizeof( linkList ) );
	tail = *l;		//tail始终指向尾节点, 开始时指向头节点
	for( i = 0;; i < n; i++ ){
		cur = ( linkList* )malloc( sizeof( linkList ) );
		cur->next = a[i];
		tail->next = cur;
		tali = cur;
	}
	tail->next = NULL;
}

线性表基本运算在单链表上的实现

1. 初始化线性表

void
initList( linkList **l )
{
	( *l ) = ( linkList* )malloc( sizeof( linkList ) );
	( *l )->next = NULL;
}

2. 销毁线性表

void
destroyList( linkList *l )
{
	linkList *pre = l, *p = l->next;
	while( p != NULL ){
		free( pre );
		pre = p;
		p = pre->next;
	}
	free( pre );
}

时间复杂度为O(n)

3. 判断线性表是否为空表

int
listEmpty( linkList *l )
{
	return ( l->next == NULL );
}

4. 求线性表的长度

单链表没有像顺序表那样有单独存放长度的空间，求链表长度时需要遍历链表。

int
listLength( linkList *l )
{
	int cnt = 0;
	while( l->next != NULL ){
		cnt++;
		l = l->next;
	}

	return cnt;
}

时间复杂度为O(n)

5. 输出线性表

void
dispList( linkList *l )
{
	for( l = l->next; l ！= NULL; l = l->next ){
		printf("%d", l->data );
	}
}

6. 求线性表L中位置i的数据元素

存在返回1，否则返回0

#define TRUE  1
#define FALSE 0

int
getElem( linkList *l, int i, int *e )
{
	int j;
	while( j < i && l != NULL ){
		j++;
		l = l->next;
	}
	if( l == NULL ){
		return FALSE;
	}else{
		*e = l->data;
		return TRUE;
	}
}

时间复杂度为O(n)，链表不具有随机存取特性

7. 按元素值查找

int
locateElem( linkList *l, int key )
{
	int i = 1;
	for( l = l->next; l != NULL && l->data != key; l = l->next, i++ ){
		;
	}
	if( l != NULL ){
		return 0;
	}else{
		return i;
	}
}

8. 插入数据元素

将值为x的新节点*s，插入到 *p节点之后
特点：只需要修改相关指针，不需要移动节点

#define TRUE  1
#define FALSE 0

int
listInsert( linkList *l, int i, int e )
{
	int j = 0;
	linkList *n;
	while( j < i - 1 && l != NULL ){
		j++;
		l = l->next;
	}
	if( l == NULL ){
		return FALSE;
	}else{
		n = ( linkList* )malooc( sizeof( linkList ) );
		n->data = e;
		n->next = p->next;
		p->next = n;
		return TRUE;
	}
}

9. 删除数据元素

删除*p节点之后的一个节点
特点：只需修改相关节点的指针，不需要移动节点

#define TRUE  1
#define FALSE 0

int
listDelete( linkList *l, int i )
{
	int j = 0;
	linkList *tl;
	while( j < i - 1 && l != NULL ){
		j++;
		l = l->next;
	}
	if( l == NULL ){
		return FALSE;
	}else{
		tl = l->next;
		if( tl == NULL ){
			return FALSE;
		}
		l->next = tl->next;
		free( tl );
		return TRUE;
	}
}

链表的优劣

优点	缺点
由于采用动态内存分配的方式，具有良好的适应性	存储密度小
插入和删除只需修改相关指针域，不需要移动元素	不具有随机存取特性

线性表的顺序存储结构和链式存储结构有何差异？

1. 线性表顺序存储结构是地址空间是连续的，链式结构不一定连续

2. 顺序结构可以实现随机存取，但是删除插入不方便，需要移动大量元素，链式结构无法随机存取（必须从头开始找），但是删除、插入比较方便

3. 顺序结构存储密度高，链式存储密度低

拓展阅读

https://blog.csdn.net/WWIandMC/article/details/105215361

单链表的特点

当访问过一个节点后，只能接着访问它的后继节点，无法访问它的前趋节点。一条路走到黑。在设计算法时要时刻牢记单链表的这条特性