顺序队

队列

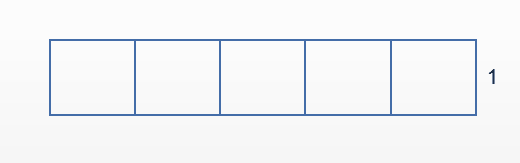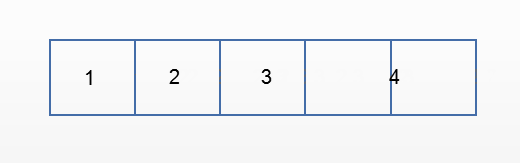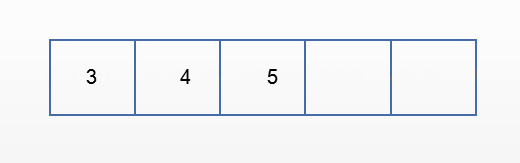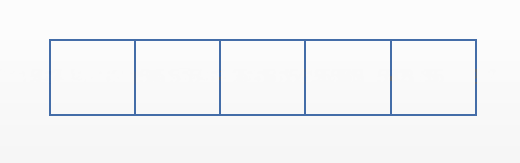
和栈一样，队列也是一种运算受限的线性表。队列只能选取一个端点进行插入操作，另一个端点进行删除操作。

• 进行插入操作的一端称为队尾
• 进行删除操作的一端称为队头
• 向队列中插入新元素的操作称为进队，新元素进队后成为新的队尾元素
• 从队列中删除元素的操作称为出队，元素出队后，其后继元素成为队首元素

队列的特点是先进先出 ( First In First Out ) ，因此又把队列称为先进先出表。

队列的顺序存储结构

typedef struct _sqQueue{
	ElemType data[SIZE];
	int front;
	int rear;
}sqQueue;

• rear指向队尾元素，front指向队头元素的前一个位置
• 进队rear++，出队front++
• 当front == rear为true时，队空
• 当rear == SIZE - 1为true时，队满

顺序队的基本运算

初始化队

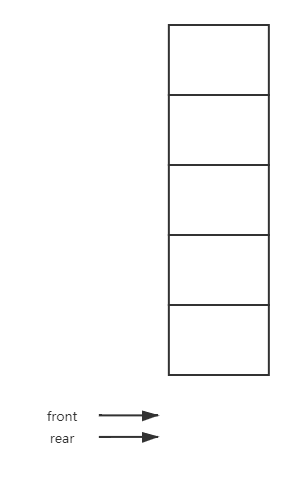
在堆中申请一块连续的内存空间用于存放数据，front和rear初始化为-1

void
initQueue( sqQueue **q )
{
	*q = ( sqQueue* )malloc( sizeof( sqQueue ) );
	(*q)->front = (*q)->rear = -1;
}

销毁队

调用free函数释放申请的内存空间

#define destroyQueue(q) free(q)

判断队是否为空

当front和rear指向同一个位置时，队列为空

#define queueEmpty(q) ( q->front == q->rear )

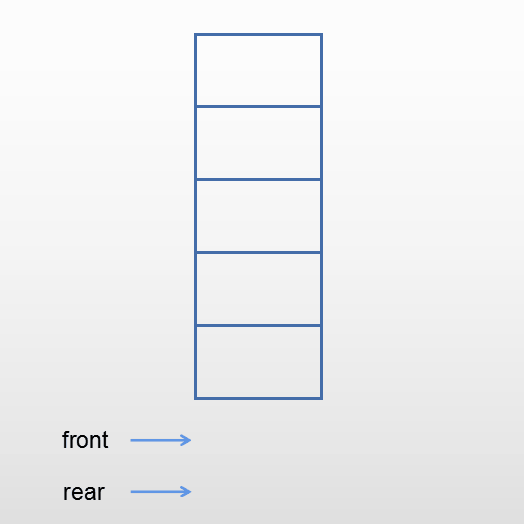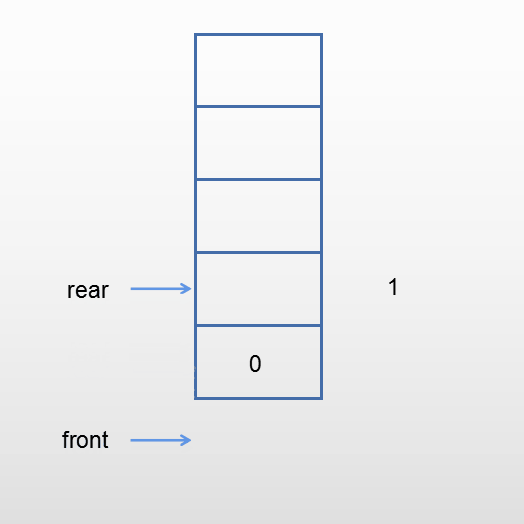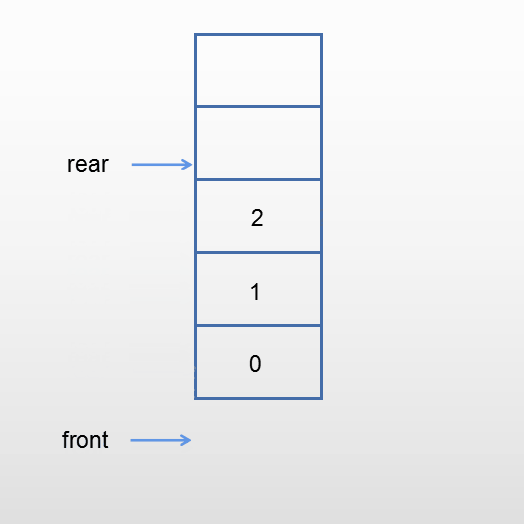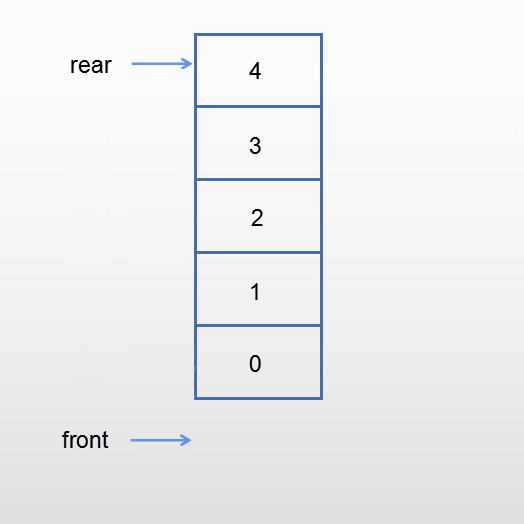
进队

当队列未满时，新元素从队尾进入队列。rear加1指向下一个位置，新元素写入rear指向的位置

int
enQueue( sqQueue *q, int e )
{
	if( q->rear == SIZE - 1 ){
		return FALSE;
	}
	q->data[ ++q->rear ] = e;
	return TRUE;
}

出队

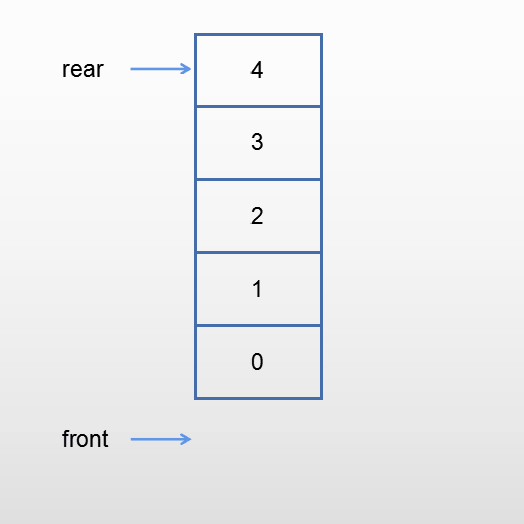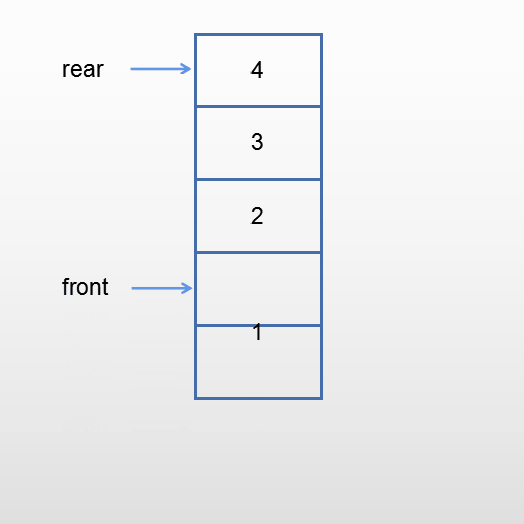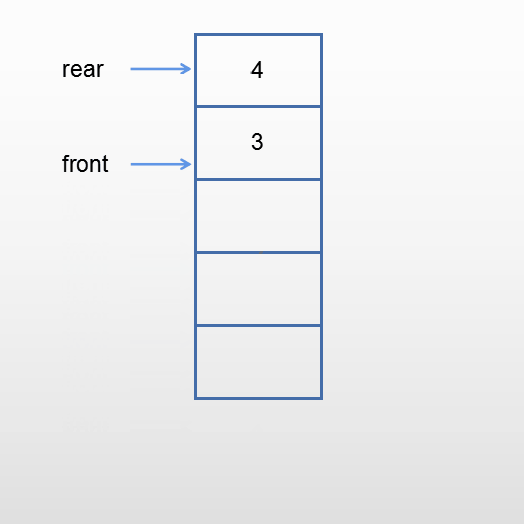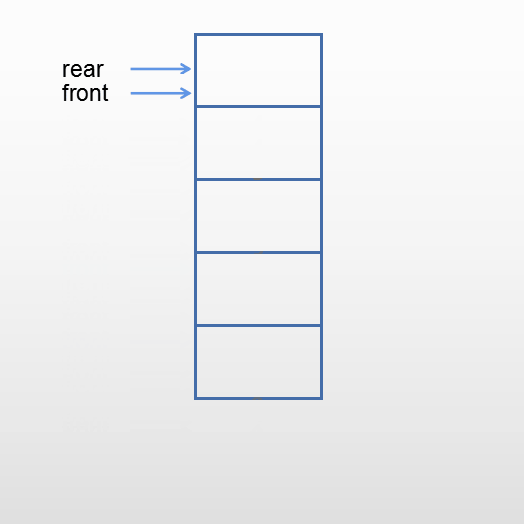
当队不为空时，元素从队头离开。front指向后继元素的前一个位置。

int
deQueue( sqQueue *q, int *e )
{
	if( q->front == q->rear ){
		return FALSE;
	}
	*e = q->data[ ++q->front ];
	return TRUE;
}

循环队列

在上面的示例中，当rear指向了数组最后一个位置，则判断队列为满。此时即使执行出队操作腾出空间，也没有破坏队满的条件，新的元素无法进队。

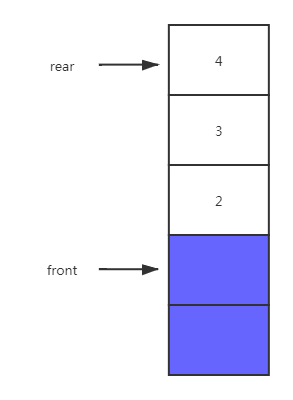
这种情况称之为假溢出。要把蓝色部分的空间利用起来，需要改进算法。

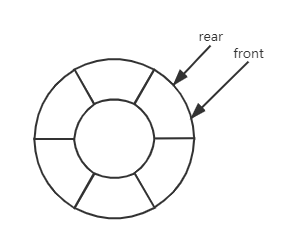
解决方案是：在逻辑上把队列看成是首尾相接的（在物理上并不相连），元素进队和出队看成是在一个环形结构中进行。

在循环队列中，用rear和front的相对距离来判断队空和队满
如图所示，front和rear的距离有6种情况：
$$0,1,2,3,4,5$$
即大小为n的队列，front和rear的距离有n种可能

队列元素个数有7种情况：
$$0,1,2,3,4,5,6$$
即大小为n的队列，元素个数有n+1种可能。

front和rear距离的n种可能不能完全表示队列n+1种状态。
解决这个问题有两种方案：

1. 仅使用n-1个数组空间，让队列的元素个数只有n种可能，数组仅有一个空闲单元即为满。
2. 使用额外标记cnt来记录当前队列的元素个数，cnt == SIZE为满。

解决方案一

• 进队操作
  rear = ( rear + 1 ) % SIZE
• 出队操作
  front = ( front + 1 ) % SIZE
• 队空条件
  front == rear为true
• 队满条件
  ( rear + 1 ) % SIZE == front为true

初始化队

front和rear初始化为0

void
initQueue( cyQueue **q )
{
	*q = ( cyQueue* )malloc( sizeof( cyQueue ) );
	(*q)->front = (*q)->rear = 0;
}

进队

int
enQueue( cyQueue *q, int e )
{
	if( ( q->rear + 1 ) % SIZE == q->front ){
		return FALSE;
	}
	q->rear = ( q->rear + 1 ) % SIZE;
	q->data[ q->rear ] = e;
	return TRUE;
}

出队

int
deQueue( cyQueue *q, int *e )
{
	if( q->rear == q->front ){
		return FALSE;
	}
	q->front = ( q->front + 1 ) % SIZE;
	*e = q->data[ q->front ];

	return TRUE;
}

解决方案二

对于循环队列来说，如果知道队头指针和队列中元素的个数，则可以计算出队尾指针。也就是说可以用队列中元素个数代替队尾指针。

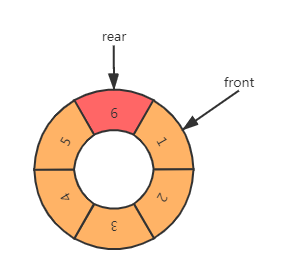
当rear > front时，元素个数等于rear - front
当rear < front时，元素个数分布在两处，SIZE - front和0 + rear
两种统一起来便是

• cnt = ( rear - front + SIZE ) % SIZE
• rear = ( front + cnt ) % SIZE
• front = ( rear - cnt + SIZE ) % SIZE

初始化队

void
initQueue( cyQueue **q )
{
	*q = ( cyQueue* )malloc( sizeof( cyQueue ) );
	(*q)->front = (*q)->cnt = 0;
}

进队

int
enQueue( cyQueue *q, int e )
{
	int rear;
	if( q->cnt == SIZE ){
		return FALSE;
	}else{
		rear = ( q->front + q->cnt ) % SIZE;
		rear = ( rear + 1 ) % SIZE;
		q->data[ rear ] = e;
		q->cnt++;
		return TRUE;
	}
}

出队

int
deQueue( cyQueue *q, int *e )
{
	if( q->cnt == 0 ){
		return FALSE;
	}else{
		q->front = ( q->front + 1 ) % SIZE;
		*e = q->data[ q->front ];
		q->cnt--;
		return TRUE;
	}
}

判断是否为空

#define queueEmpty(q) ( q->cnt == 0 )

Notice

• 环形队列比非循环队列的空间利用率更高，不会出现假溢出
• 并不是任何时候都要使用循环队列，进队的元素可能会被覆盖。如果算法需要使用所有进队的元素来进一步求解，应该使用非循环队列