哈夫曼树
定义
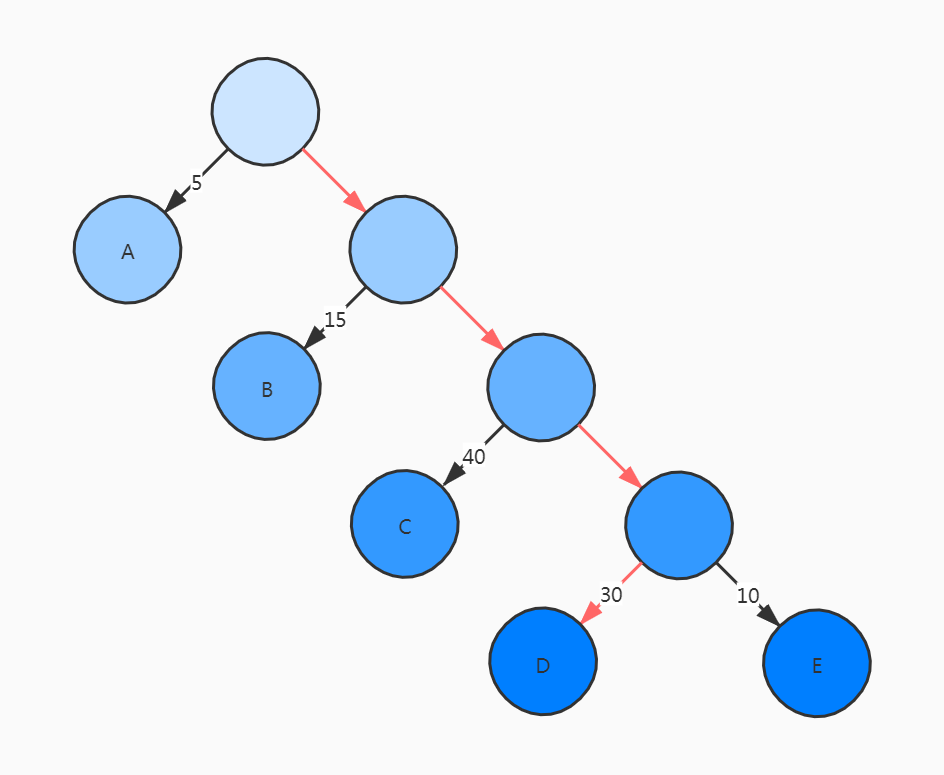
从树中一个节点到另一个节点之间的分支构成两个节点之间的路径
路径上的分支数目称为路径长度。如图所示,根节点到节点D的路径长度为4。
树的路径长度就是从树根到每一个节点的路径长度之和
a
树
的
路
径
长
度
=
1
+
1
+
2
+
2
+
3
+
3
+
4
+
4
=
20
\begin{aligned} a树的路径长度 &= 1+1+2+2+3+3+4+4\\ &=20 \end{aligned}
a树的路径长度=1+1+2+2+3+3+4+4=20
设二叉树具有n个带权值的叶子节点,那么从根节点到各个叶子节点的路径长度l与相应节点权值的w乘积的和,叫做二叉树的带权路径长度
W
P
L
=
∑
i
=
1
n
w
i
l
i
WPL = \displaystyle\sum^n_{i=1}w_il_i
WPL=i=1∑nwili
其中,将具有最小带权路径长度的二叉树称为哈夫曼树,也称最优树
a
的
W
P
L
=
5
×
1
+
15
×
2
+
40
×
3
+
30
×
4
+
10
×
4
=
315
\begin{aligned} a的WPL&=5 \times 1 + 15 \times 2 + 40 \times 3 + 30 \times 4 + 10 \times 4\\ &=315 \end{aligned}
a的WPL=5×1+15×2+40×3+30×4+10×4=315
构造哈夫曼树
- 权值越大的叶子节点越要靠近根节点
- 权值越小的叶子节点越要远离根节点
序列{A5,B15,C40,D30,E10},字母后的数字为权重
-
以权值递增顺序重新排列
A5,E10,B15,D30,C40 -
取序列中前两个权值最小的节点作为新节点
N1的两个孩子节点,权值小的是左孩子,权值大的是右孩子
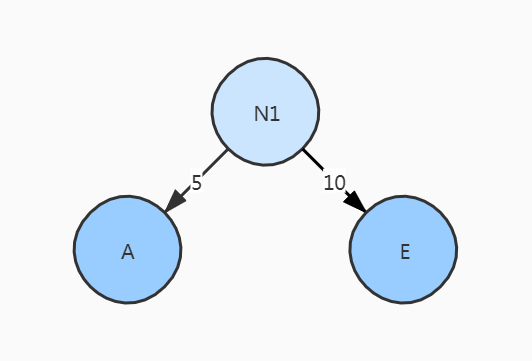
-
新节点
N1的权值是两个孩子节点的权值之和,即5+10=15。用(N1)15替换A5和E10,插入到有序序列中,保持从小到大排列
(N1)15,B15,D30,C40 -
取前两个权值最小的节点
(N1)15,B15
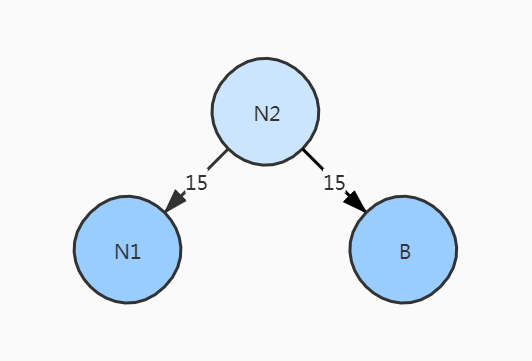
用(N2)30替换(N1)15和B15,插入到有序序列中
(N2)30,D30,C40 -
取前两个权值最小的节点
(N2)30,D30
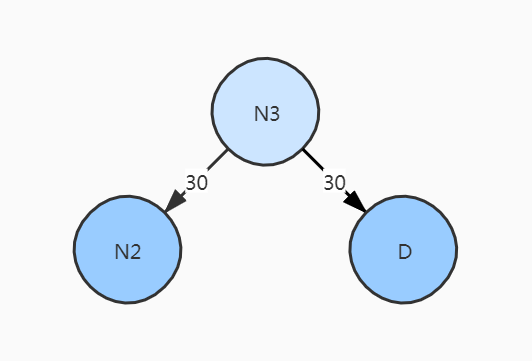
用(N3)60替换(N2)30和D30,插入到有序序列中,注意保持从小到大的排列
C40,(N3)60
- 取前两个权值最小的节点
C40,(N3)60
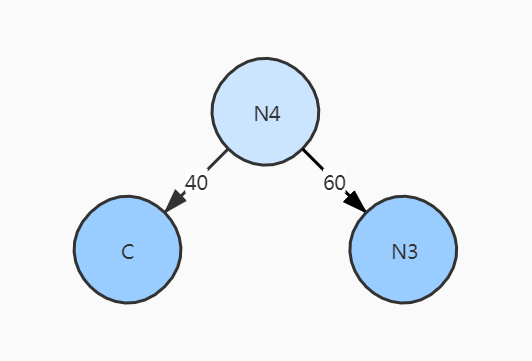
替换完成后序列只有N4一个节点,哈夫曼树构造完成
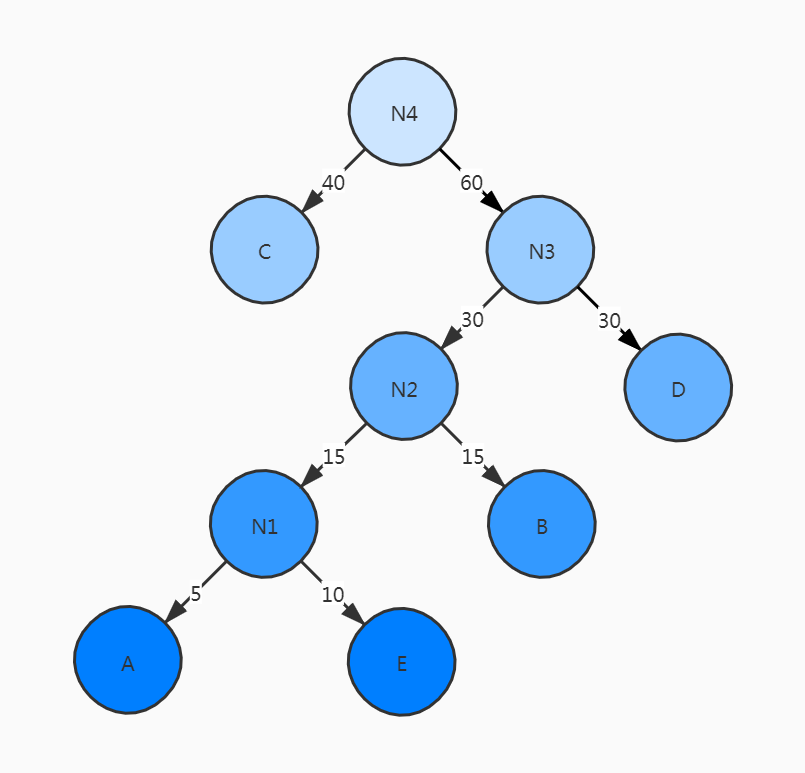
此 时 的 W P L = 40 × 1 + 30 × 2 + 15 × 3 + 10 × 4 + 5 × 4 = 205 \begin{aligned} 此时的WPL&=40 \times 1 + 30 \times 2 + 15 \times 3 + 10 \times 4 + 5 \times 4\\ &=205 \end{aligned} 此时的WPL=40×1+30×2+15×3+10×4+5×4=205
哈夫曼树的特点
哈夫曼树没有单分支节点,即度为1的节点n1的数目等于0
所以
n
=
n
0
+
n
1
+
n
2
=
n
0
+
n
2
=
2
n
0
−
1
n = n_0 + n_1 + n_2\\ = n_0 + n_2\\ =2n_0 - 1
n=n0+n1+n2=n0+n2=2n0−1
哈夫曼编码
现有序列 DBACADFEED
采用二进制来传输信息
| A | 000 |
| B | 001 |
| C | 010 |
| D | 011 |
| E | 100 |
| F | 101 |
011001000010000011101100100011
采用哈夫曼编码的方法,先分析字符在字符串中的权重
| 占比 | 放大100倍的权值 | |
|---|---|---|
| A | 0.20 | 20 |
| B | 0.10 | 10 |
| C | 0.10 | 10 |
| D | 0.30 | 30 |
| E | 0.20 | 20 |
| F | 0.10 | 10 |
构造哈夫曼树
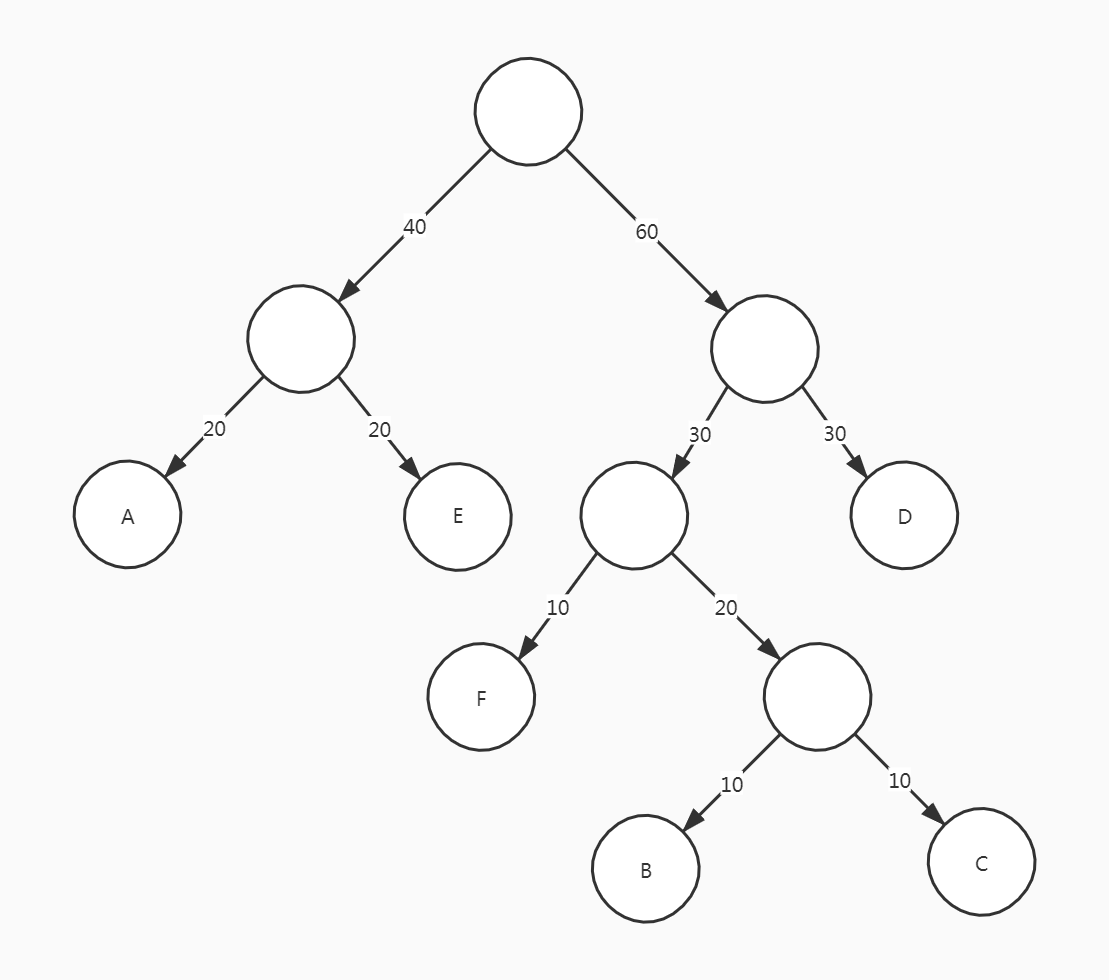
规定哈夫曼树中的左分支为0,右分支为1
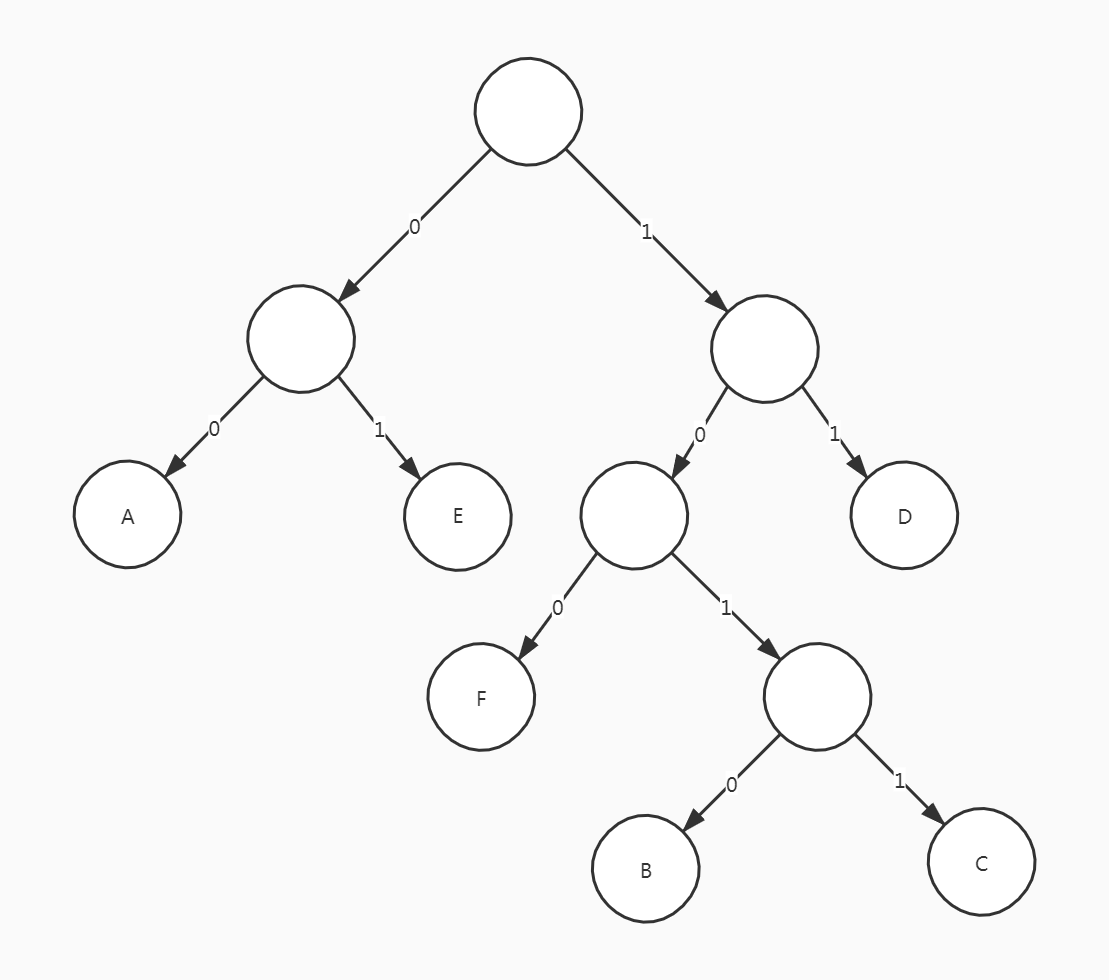
从根节点到每个叶子节点所经过的分支对应的0和1组成的序列便为该节点对应字符的编码。这样的编码称为哈夫曼编码。
| A | 00 |
| B | 1010 |
| C | 1011 |
| D | 11 |
| E | 01 |
| F | 100 |
得到哈夫曼编码
1110100010110011100010111
比原来少了5个字符。
前缀编码
在一组字符的哈夫曼编码中,不可能出现一个字符的哈夫曼编码是另一个字符哈夫曼编码的前缀。上面的表格就不存在容易与1010混淆的101
- 没有两个字符的编码相同
- 没有两个字符编码的前缀相同
例1
5个字符有如下4种编码方法,其中不是前缀编码的是
A. 01,0000,0001,001,1
B. 011,000,001,010,1
C. 000,001,010,011,100
D. 0,100,110,1110,1100
D选项中110和1100前缀重复,不是前缀编码
例2
对n( n ≥ 2 )个权值均不同的字符构成哈夫曼树,关于该树的叙述中,错误的是
A. 该树一定是一棵完全二叉树
B. 该树中一定没有度为1的节点
C. 树中两个权值最小的节点一定是兄弟节点
D. 树中任一非叶子节点的权值一定不小于下一层任一节点的权值
选A
例3
如果一棵哈夫曼树T中共有255个节点,那么该树用于对几个字符进行哈夫曼编码
解:
没有度为1的节点
n = 2n0 - 1推出n0 = 128
按照哈夫曼树的定义,叶子节点即为字符,所以该树用于对128个字符进行哈夫曼编码


 浙公网安备 33010602011771号
浙公网安备 33010602011771号