最小生成树 Kruskal

Kruskal算法比起Prim算法还要更贪心一些

Prim算法以某个顶点为起点，在这个顶点附近找权重最小的边；而Kruskal算法只要当前图中权重最小的边

Kruskal算法

Kruskal算法的思路是：把森林合并成树

最开始时，我们把所有的顶点看做是一棵树的根节点，总共有n棵树

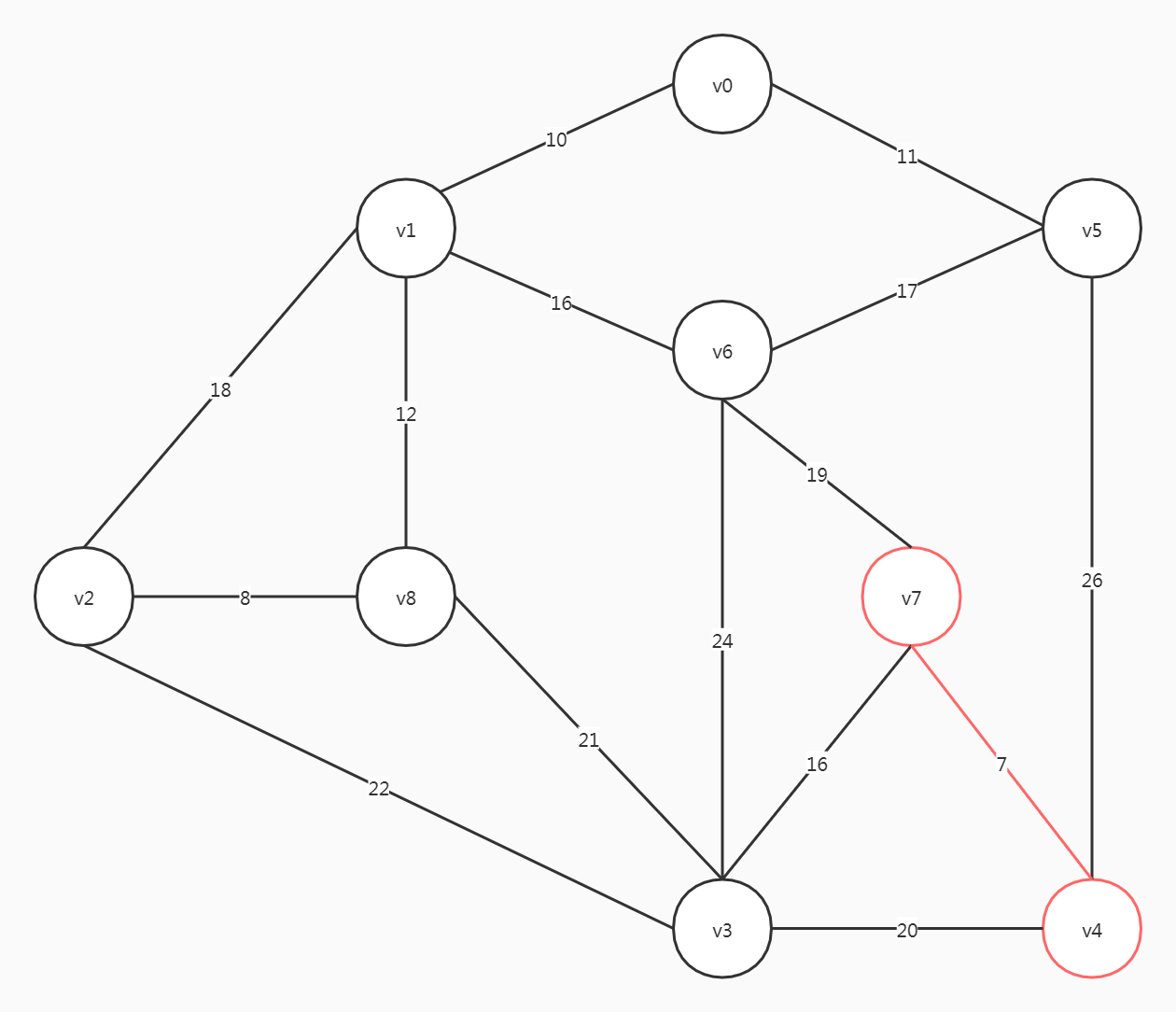
整个图中，(v4, v7)的权重是最小的，从这里开始

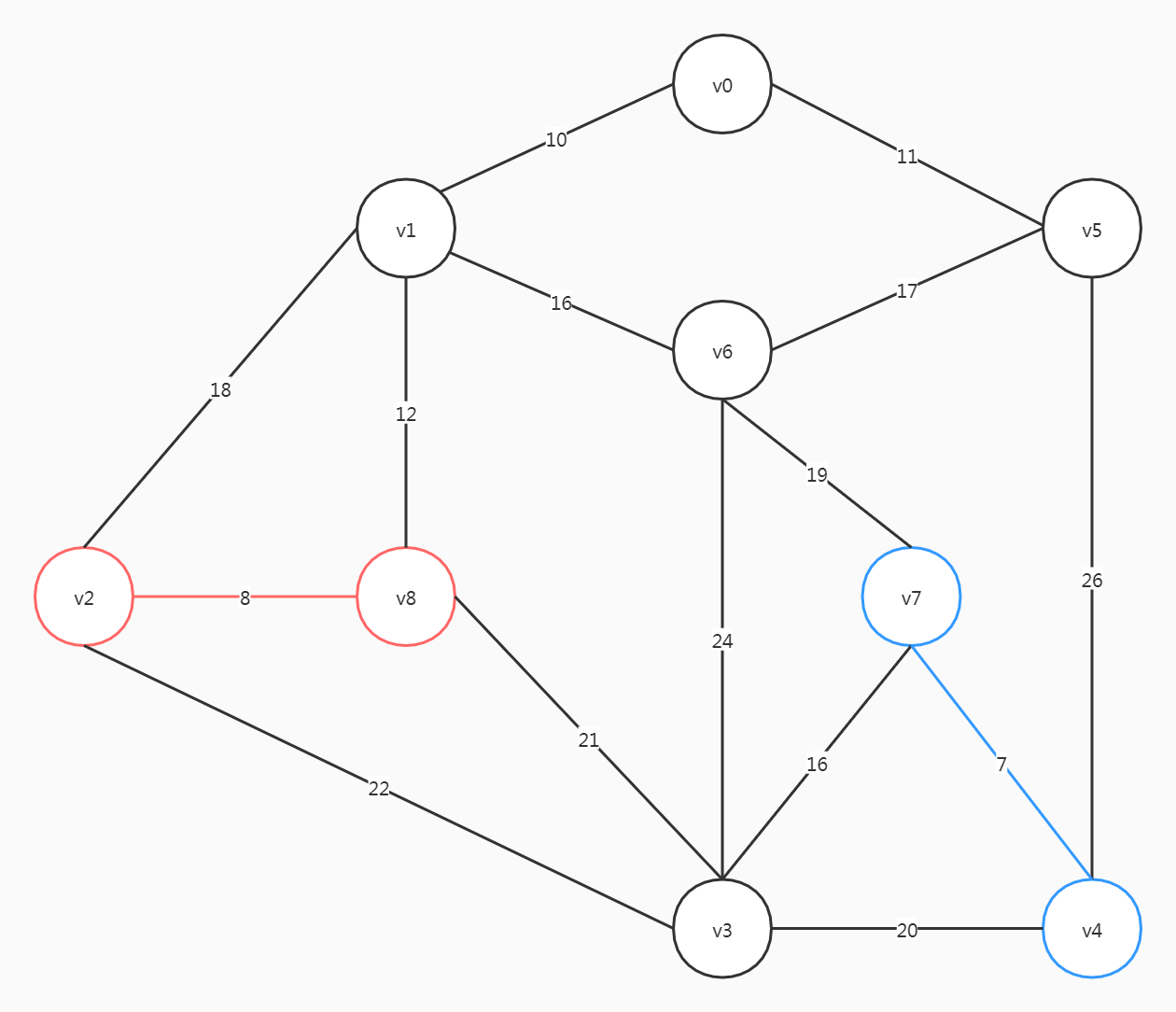
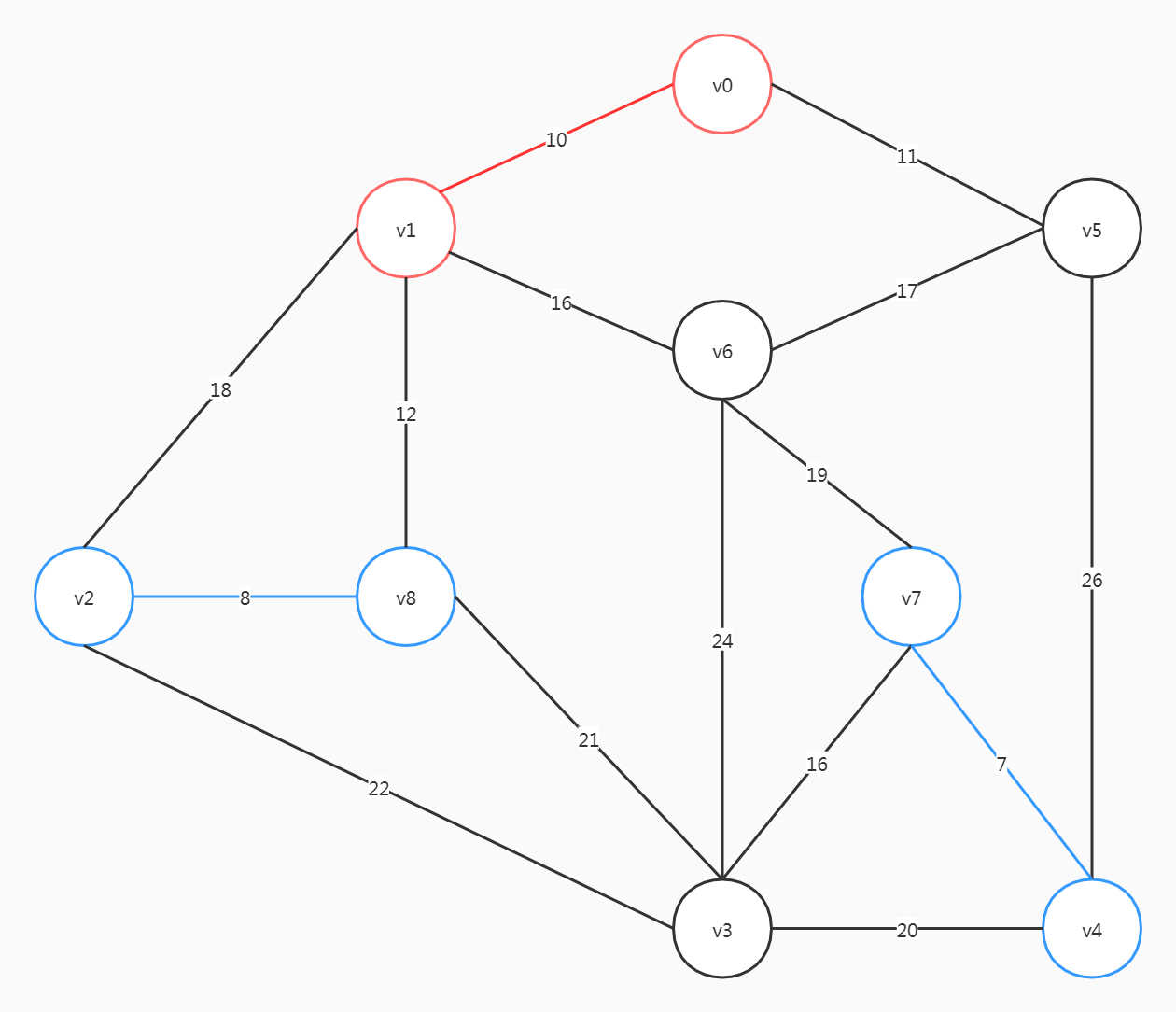
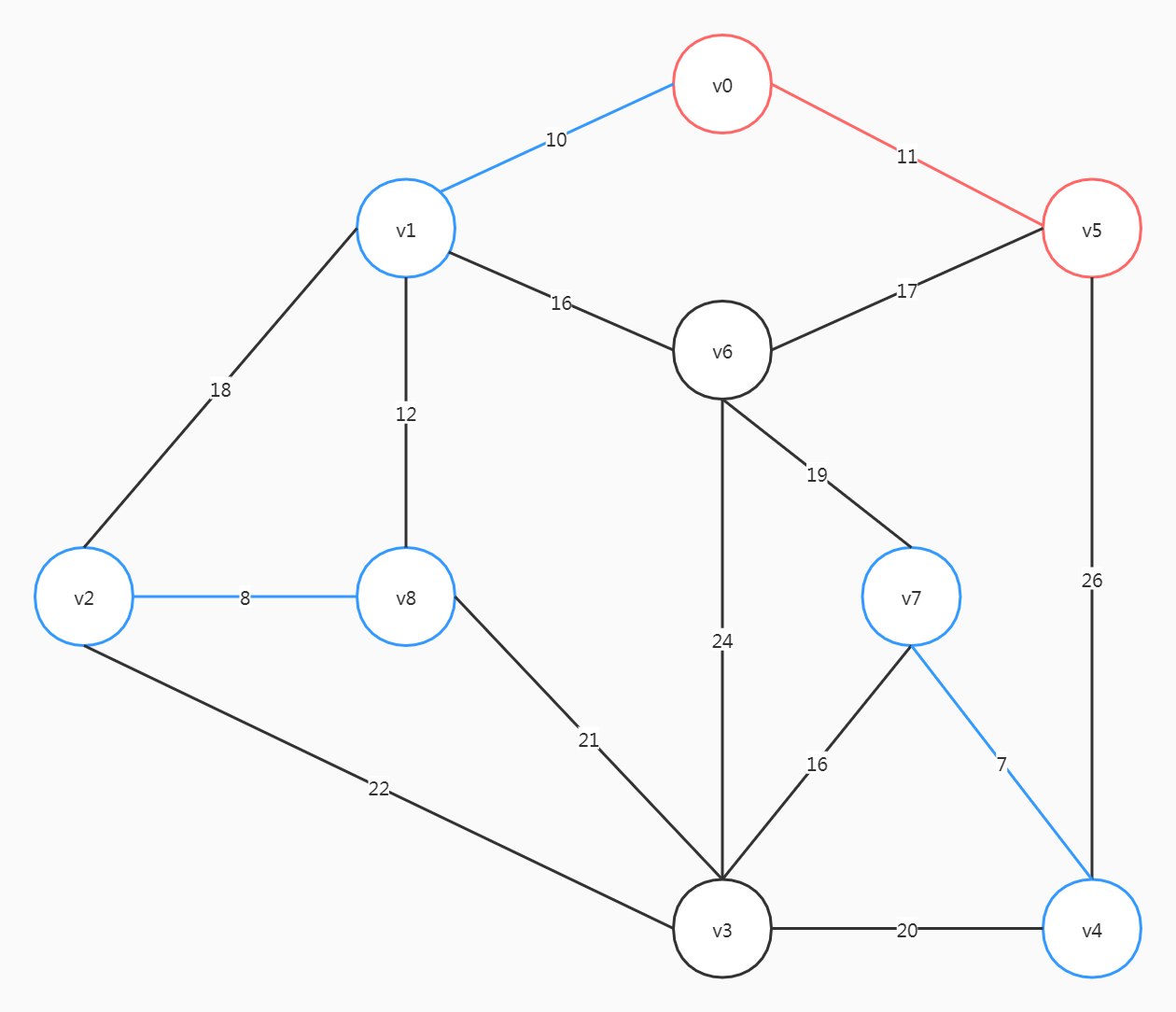
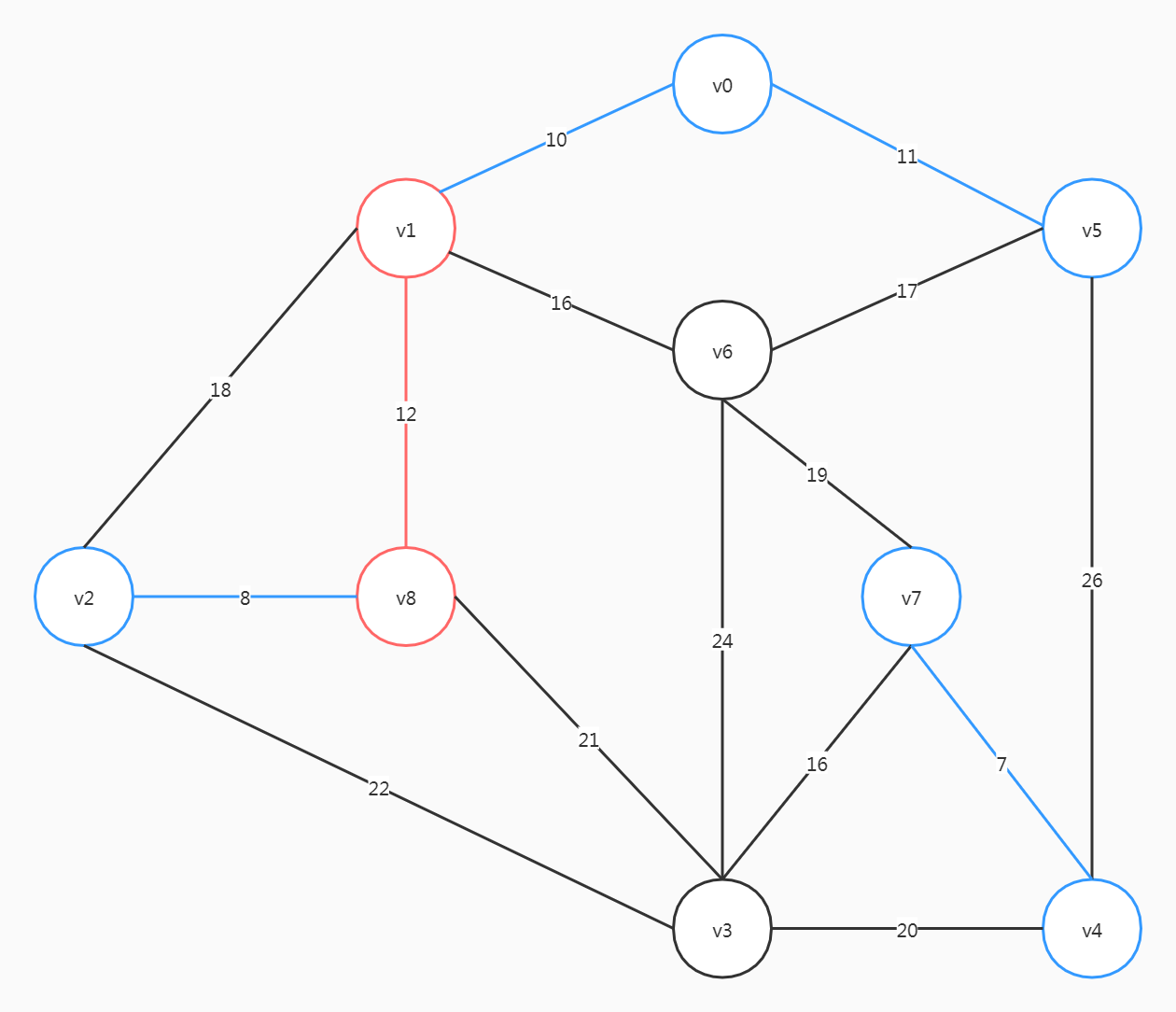
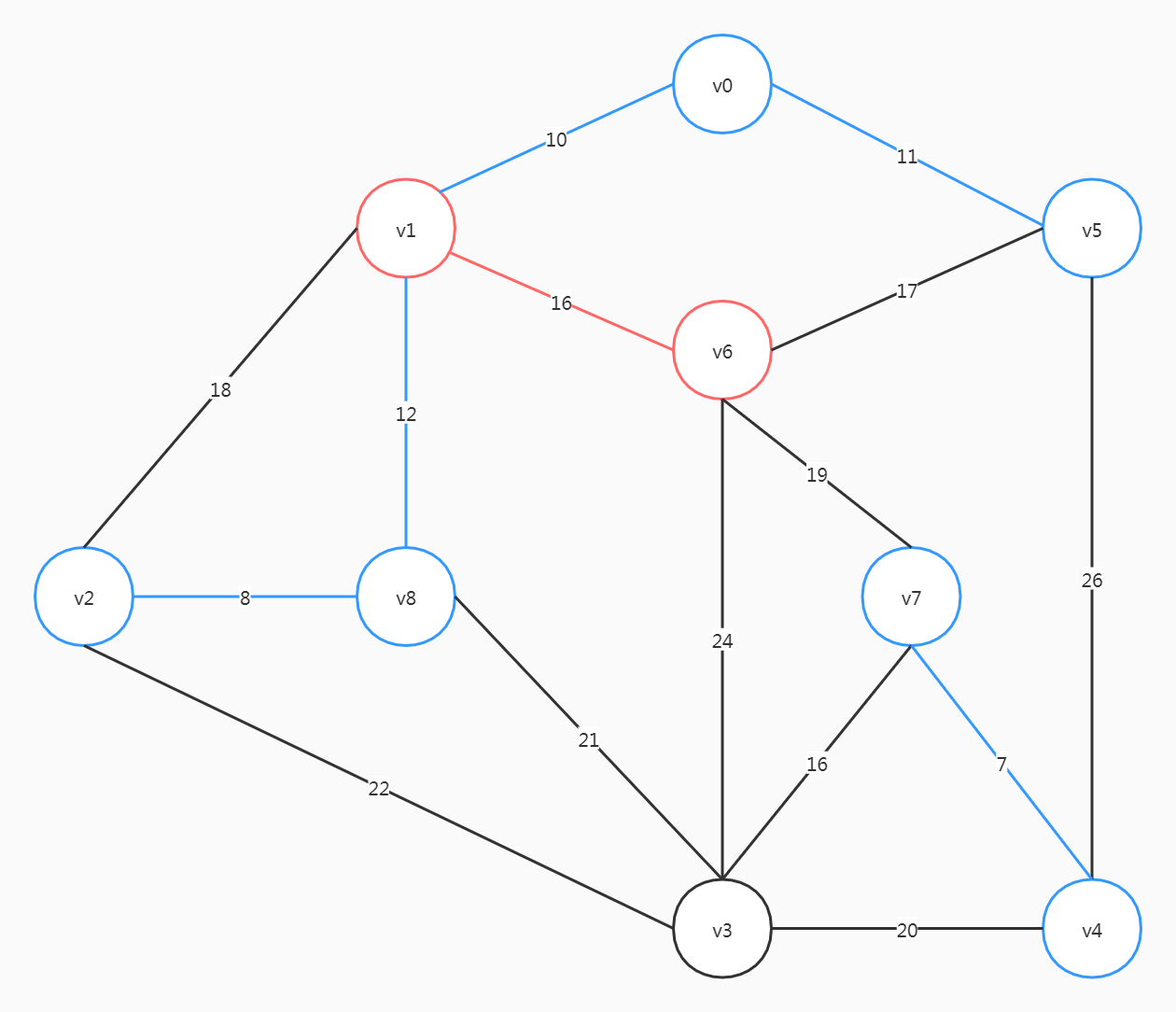
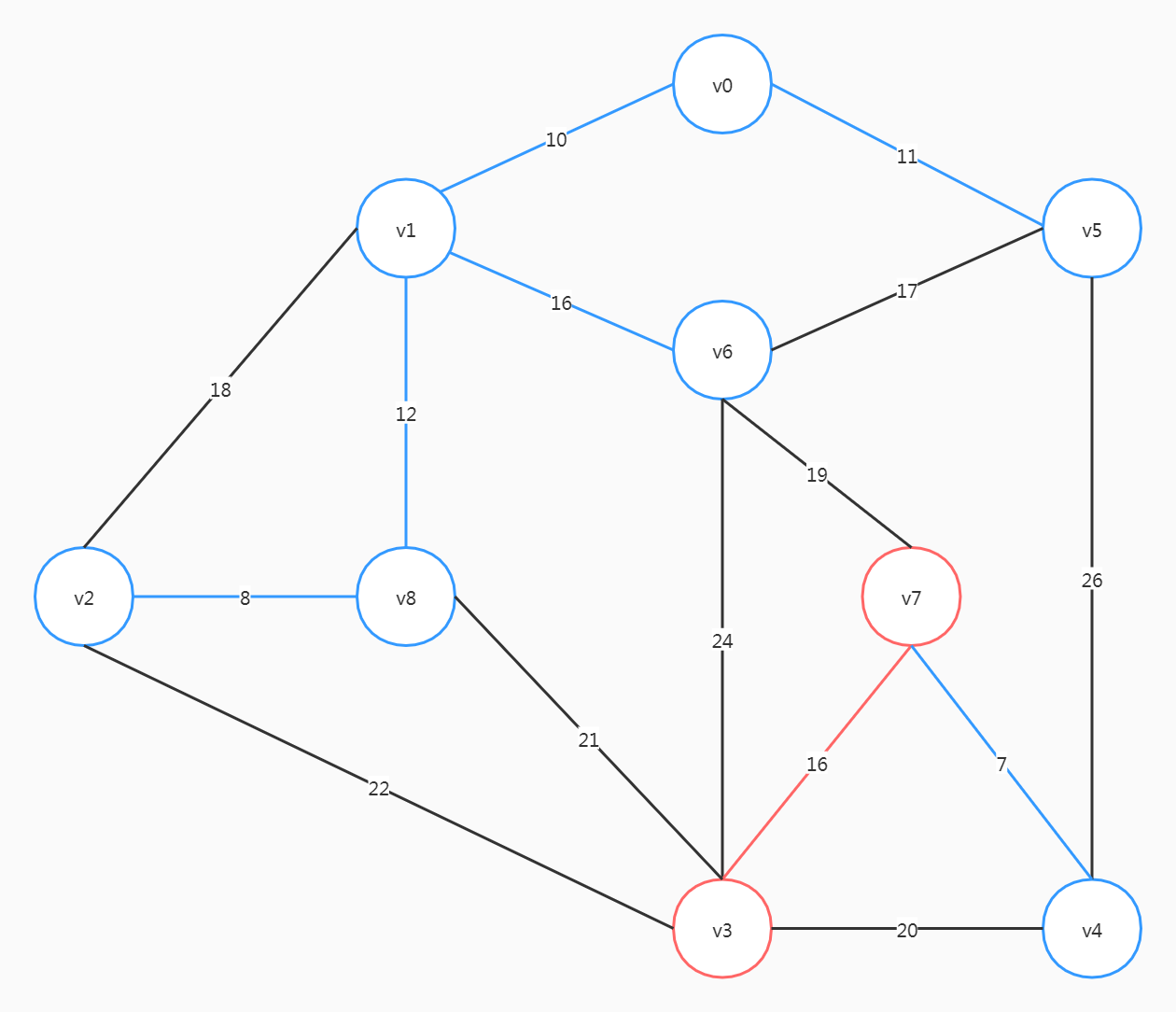
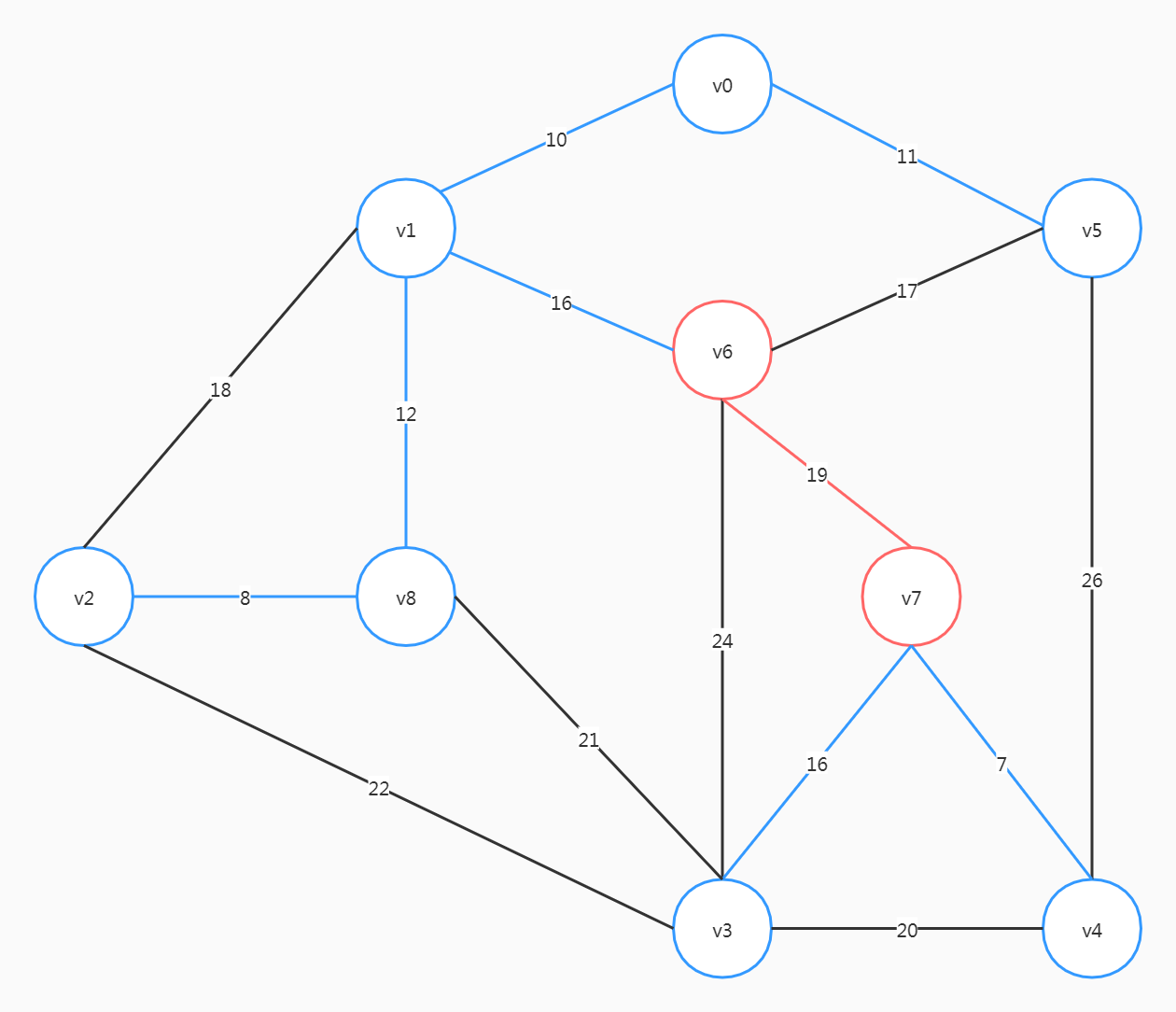
这里要注意，尽管(v6, v5)、(v2, v1)的权重比(v6, v7)小，但选了前两个会形成回路

至此，最小生成树构建完成

存储结构

在Kruskal算法中，使用边集数组，提高对边处理的效率

typedef struct _edge {
    int begin;
    int end;
    int weight;
}edge;

边集合按照边集数组形式存储，每条边按照权重从小到大顺序排列

edge	begin	end	weight
0	0	1	10
1	0	5	11
2	1	2	18
3	1	6	16
4	1	8	12
5	2	3	22
6	2	8	8
7	3	4	20
8	3	6	24
9	3	7	16
10	3	8	21
11	4	5	26
12	4	7	7
13	5	6	17
14	6	7	19

加上顶点集合就是一张完整的图

typedef int VexType;
typedef struct _egraph {
    VexType* vex;
    edge* Arc;
    int num_vexs;
    int num_edge;
}egraph;

输入

• 第一行给出顶点个数和边的条数
• 第二行给出顶点元素的值
• 之后给出边集数组，数据按照下面的格式给出

起点	终点	权重

9 14
0 1 2 3 4 5 6 7 8
4 7	7
2 8	8
0 1 10
0 5	11
1 8	12
1 6	16
3 7	16
5 6	17
1 2	18
6 7	19
3 4	20
3 8	21
2 3	22
3 6	24
4 5	26

图的转化和排序是Kruskal算法的一部分，为了偷懒 简化把这部分工作扔给输入了

void MST_Kruskal(egraph* e) {
    int* parent;  // 用来判断边与边是否会形成回路
    parent = new int[e->num_vexs]();   //加上圆括号调用构造函数, 初始化数组全为0
    int m, n;
    for (int i = 0; i < e->num_edge; i++) {
        n = find(parent, e->Arc[i].begin);
        m = find(parent, e->Arc[i].end);
        if (n != m) {   //不相等说明没有形成回路, 将这条边并入MST
            parent[n] = m;
            cout << e->Arc[i].begin << ' ' << e->Arc[i].end << ' ' << e->Arc[i].weight << endl;
        }
    }
    delete[] parent;
}

int find(int* parent, int f) {  //从给定的节点向其根节点回溯, 找到连线的尾巴
    while (parent[f] > 0) {
        f = parent[f];
    }
    return f;
}

假设有总共有n条边
find()的时间复杂度
$$O(lo{g}_{2}n)$$
find()嵌套在一个时间复杂度为O(n)的for循环内

所以MST_Kruskal()的时间复杂度为
$$O(nlo{g}_{2}n)$$

输出

4 7 7
2 8 8
0 1 10
0 5 11
1 8 12
1 6 16
3 7 16
6 7 19

Prim和Kruskal的总结

• Prim适合处理稠密图
• Kruskal适合处理稀疏图