算法入门-求最大公约数、欧几里得游戏、带锁的门

参考教材：The design and Analysis on Algorithms

 

小学数学复习：最大公约数

def.两个不全为0的非负整数m和n的最大公约数gcd（m, n）是能整除m和n的最大正整数。 注：gcd = greatest common divasor

 

---

 

求最大公约数通用算法：

辗转相除法（欧几里得算法）

用较大数m除以较小数n，再用出现的余数r1去除除数n，再用出现的余数r2去除之前的余数r1……反复进行直到最后余数是0为止。

此时，最大公约数为最后的被除数。

即 gcd（m, n）→ gcd（n，m mod n）

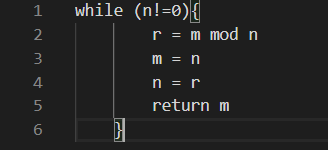
这个方法的的原理如下：

　　　　　　　　gcd(x,y)=z, 则mx+ny也可以被z整除（m、n为任意整数）

　　　　　　　若x/y=n……c（x除以y等于n余c）

 　　　　　　 则x=ny＋c

　　　　　　　　x-ny=c →此时x-ny为mx＋ny的特殊形式（m=1，n=-1）

　　　　　　　故x-ny可被z整除

　　　　　　　c可被z整除

 

---

 

辗转相减法（更相减损术）

用较大数m减较小数n，再用差m-n和n比较，用较大数减较小数……以此类推，直到差等于0为止。

此时这两个相等的数即为最大公约数。

这个方法的原理如下（本质上与除法相同）：

　　　　　　gcd(x,y)=z, 则x=az，y=bz

　　　　　　x-y=z(a-b)

　　　　　　故x-y也是z的倍数，(x-y)与x和y的最大公约数相同。

 

---

 

欧几里得游戏

Q：一开始，板子上写有两个不相等正整数。两个玩家交替写数字，每次都必须写出任意两个板上数字的差，且必须是新的数字。当玩家再也写不出数字时就输掉了游戏。请问此游戏应该先行动还是后行动？

 

A：由上述更相减损术原理可知，板上的数字必为初始数字的最大公约数的倍数。进一步可知能写的数字个数为初始数字中较大的数除以最大公约数，即可用奇偶判断先手会赢还是后手会赢。

 

---

 

带锁的门　　　　　　　

  在走廊上有n个带锁的门，从1到n依次编号。最初所有的门都是关着的。我们从门前经过n次，每次都从1号门开始。在第i次经过时（i = 1,2，…, n)我们改变i的整数倍号锁的状态；如果门是关的，就打开它；如果门是打开的，就关上它。在最后一次经过后，哪些门是打开的，哪些门是关上的？有多少打开的门？

 

从题目可知，在第k次经过时会改变k的倍数号门的状态。

既然被改变的门m编号为k的倍数，则必然有m=kx，故它一定也是x的倍数，在m分解为kx两数相乘时一定改变了两次。故无论它可以分解为多少对两数相乘，都必然会改变2的倍数次，即偶数次，门依然是关着的。

注：（不能分解的质数y也与其他数一样可以分解为1×y它本身，即只在第一次路过和第y次路过时改变状态，也改变了偶数次）

其中，完全平方数n，可分解为同一个数的平方的那种，如49=7×7，则仅在√n次路过时改变状态，只改变了奇数次状态，门是打开的。

所以，只有完全平方数编号的门会打开。