070103_条件概率与贝叶斯公式，独立性

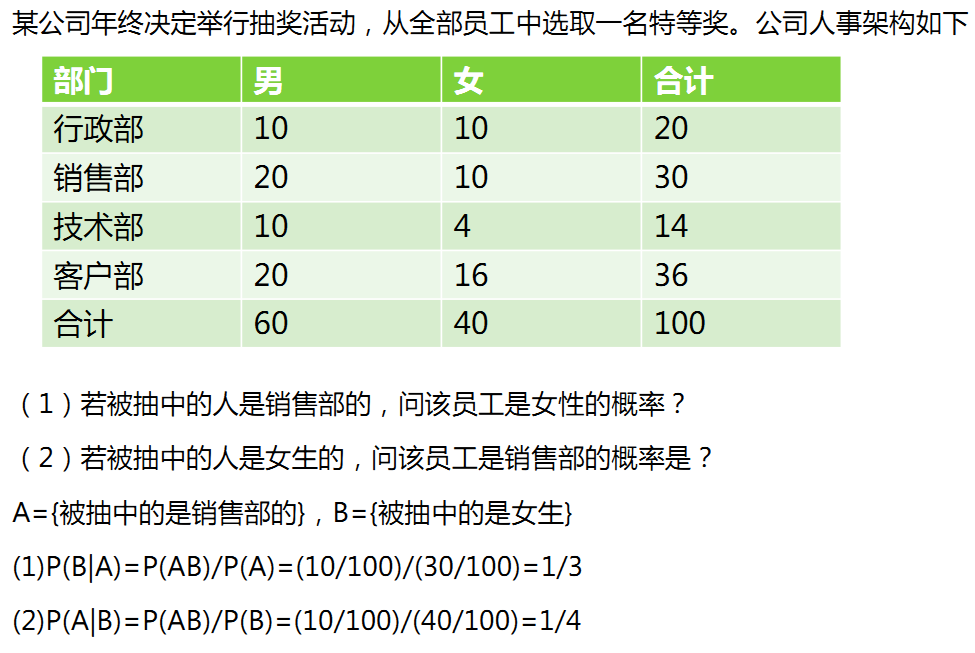
一、条件概率的计算

　　一直某个时间A发生的条件下，另一个事件B发生的概率称为条件概率，记为P（B|A）

　　p（B|A）=P（AB）/P（A）

　　条件概率也符合概率定义的三个条件。

　　

　　

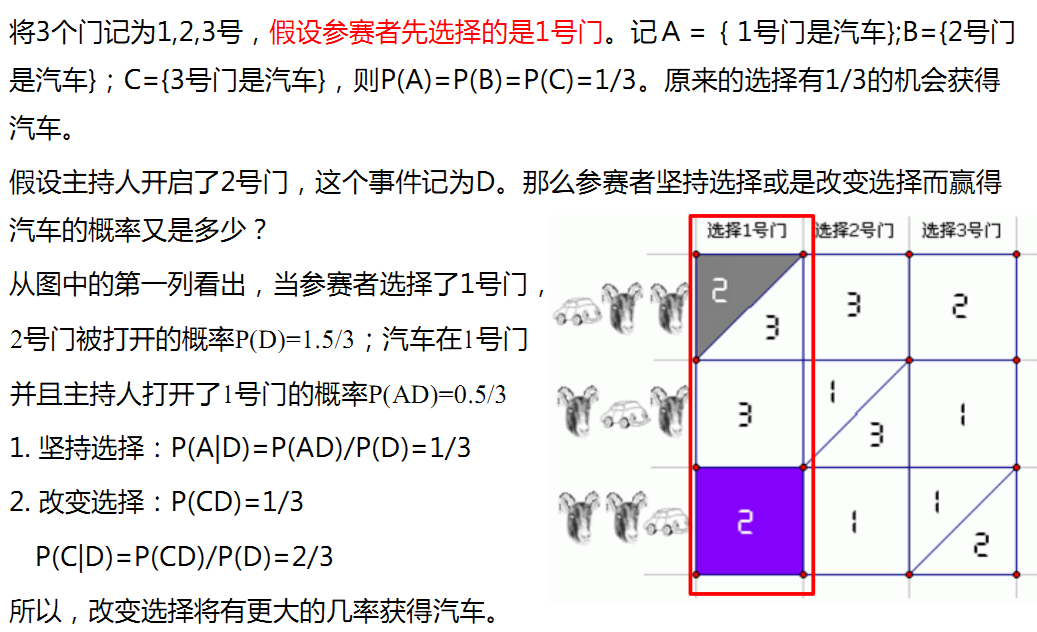
　　游戏【汽车与山羊】

　　

 

二、乘法定理

　　由条件概率的定义，很容易得到P（AB）=P（B|A）P（A），其中P（A）>0

　　推广，P（ABC）=P（C|AB）P（B|A）P（A）=P（A|BC）P(B|C)P(C)

　　

三、全概率公式

　　如果事件组B₁，B₂，.... 满足

               1.B₁，B₂....两两互斥，即 B_i ∩ B_j = ∅ ，i≠j ， i,j=1，2，....，且P(B_i)>0,i=1,2,....;

               2.B₁∪B₂∪....=Ω ，则称事件组 B₁,B₂,...是样本空间Ω的一个划分

　　设 B₁,B₂,...是样本空间Ω的一个划分，A为任一事件，则：

　　

四、贝叶斯公式

　　　

　　

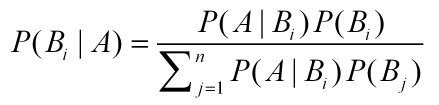
　　由以往的数据分析得到的，叫做先验概率。

　　在得到信息（即生产出的第一件产品是合格品）之后再重新加以修正的概率（即0.97）叫做后验概率。

五、公式比较

　　

六、独立性

　　

 

　　

　　

七、相互独立事件与互斥事件、对立事件