070101_描述性统计（均值，中位数，众数，方差，标准差，与常见的统计图表）

一、概率论与统计学

　　概率论是统计学的基础，统计学冲锋在应用第一线，概率论提供武器。

　　古典概率论

　　戈尔莫格洛夫创建现代概率论

　　学会和运用概率，会使人变得更聪明，决策更准确。

二、统计学

　　统计学可以分为：描述统计学与推断统计学。

　　描述统计学：使用特定的数字或图表来体现数据的集中程度和离散程度。例：每次考试算的平均分，最高分，各个分段的人数分布等，也是描述统计学的范围。

　　推断统计学：根据样本数据推断总体数据特征。例：产品质量检查，一般采用抽检，根据所抽样本的质量合格率作为总体的质量合格率的一个估计。

　　应用：统计学的应用十分广泛，可以说，只要有数据，就有统计学的用武之地。目前比较热门的应用：经济学，医学，心理学等。

 

三、集中趋势

　　均值：算数平均数，描述平均水平。

　　

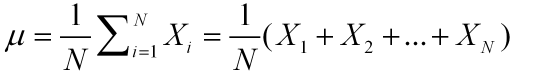
　　　　例：某次数学考试中，小组A与小组B的成员的乘机分别如下：

　　　　A：70,85,62,98,92　　B：82,87,95,80,83

　　　　分别求出两组的平均分，并比较两组的成绩。

　　　　组A：

　　　　　　

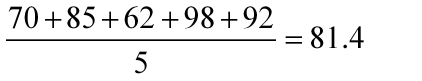
　　　　组B：

　　　　　　

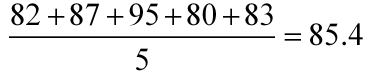
　　　　组B的平均分比组A的高，就是组B的总体成绩比组A高。

　　中位数：将数据按大小顺序（从大到小或是从小打大都可以）排列后位于中间位置的数。

　　　　例：58，32，46，92，73，88，,23

　　　　1、先排序：23，32，46，58，73，88，92

　　　　2、找出处于中间位置的数：23，32，46，58，73，88，92

　　　　若处于中间位置的数据有两个（也就是数据的总个数为偶数时），中位数为中间两个数的算术平均数。

　　众数：数据中出现最多的数（所占比例最大的数）

　　　　一组数据中，可能存在多个众数，也可能不存在众数。

　　　　1 2 2 3 3 中的众数是2和3

　　　　1 2 3 4 5 中没有众数

　　　　众数不仅适用于数值型数据，对于非数值型数据也同样适用。

　　　　{苹果，苹果，香蕉，橙，橙，橙，桃}，这一组数据，没有什么均值、中位数可言，但是存在着众数——橙。

　　均值、中位数、众数

　　

 

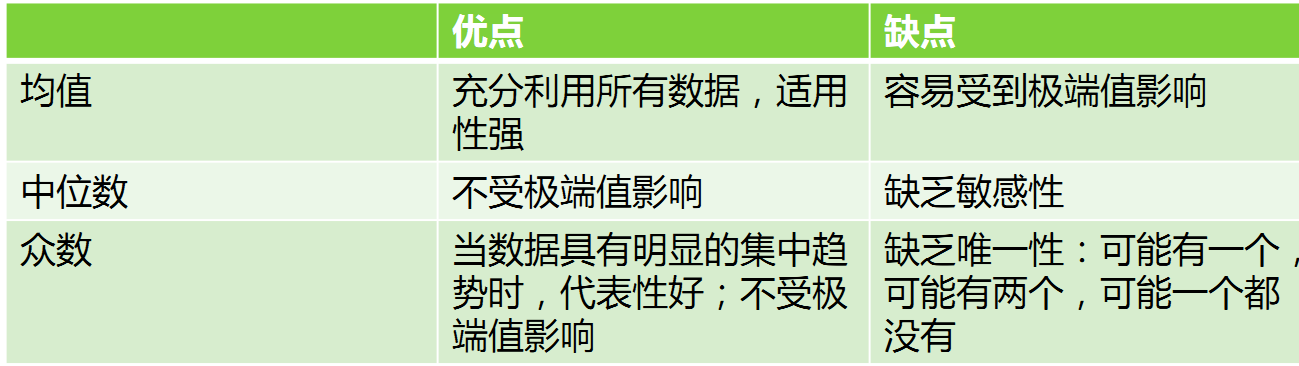
四、离散程度的描述

　　极差：最大值-最小值，简单地描述数据的范围大小，极差越大越分散。

　　方差：在统计学上，更常的是使用方差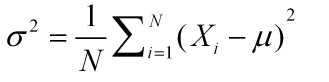来描述数据的离散程度——数据离中心越远越离散。

　　　　　其中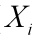，表示数据集中第 i 个数据的值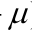，表示数据集的均值。

　　　　例：A——1 2  5 8 9

　　　　

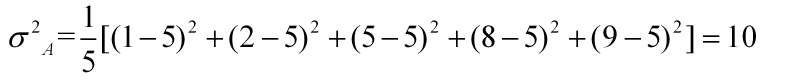
　　标准差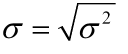：，有效地避免了因单位平方而引起的度量问题。与方差一样，标准差的值越大，表示数据越分散。

 

　　　　方差与原数据的单位是不一样的，这样的比较是无意义的。为了保持单位的一致性，引入了一个新的统计量——标准差。

 

五、直方图　　

　　只依赖数字来描述集中趋势与离散程度，让人难以对数据产生直观的印象，这时候就需要用到图表。

　　频数分布表

　　　　1、找出最大值与最小值，确定数据的范围。

　　　　2、整理数据，将数据按照成绩分为几组。

　　　　3、画表。

　　频数直方图

　　　　根据频数分布表，可以画出频数直方图。

　　频率直方图

　　　　与频数直方图相比，频率直方图纵坐标有所改变，使用了频率/组距。

　　　　频率=频数/总数，组距就是分组的极差。

 

六、箱线图

　　下四分位数：Q1，将所有数据按照从小到大的顺序排序排在第25%位置的数字。

　　上四分位数：Q3，将所有数据按照从小到大的顺序排序排在第75%位置的数字。

　　四分位距：IQR，等于Q3-Q1，衡量数据离散程度的一个统计量。

　　异常点：小于Q1-1.5IQR或大于Q3+1.5IQR的值。

　　上边缘：除异常点以外的数据中的最大值。

　　下边缘：除异常点以外的数据中的最小值。

 

七、茎叶图

　　茎叶图可以在保留全部数据信息的情况下，直观地显示出数据的分布情况。

　　左边是茎，右边是叶。

 

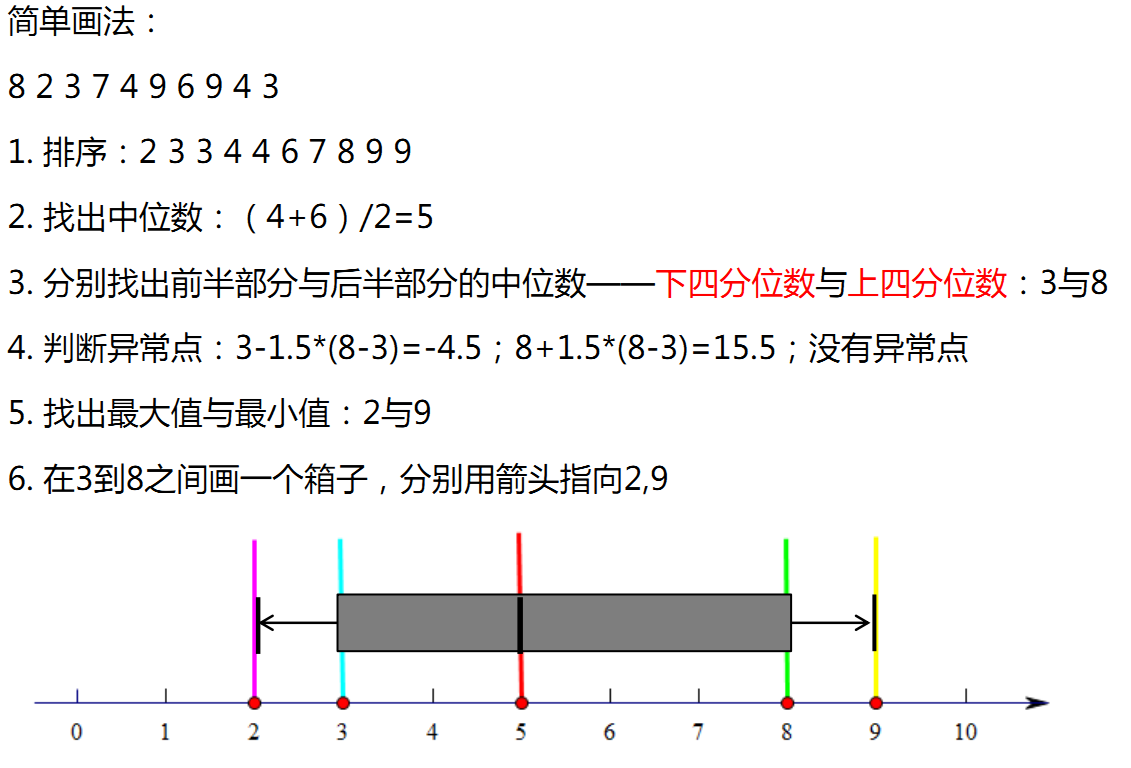
八、线图

　　以时间为横坐标，变量为纵坐标，反映变量随时间推移的变化趋势。

　

 

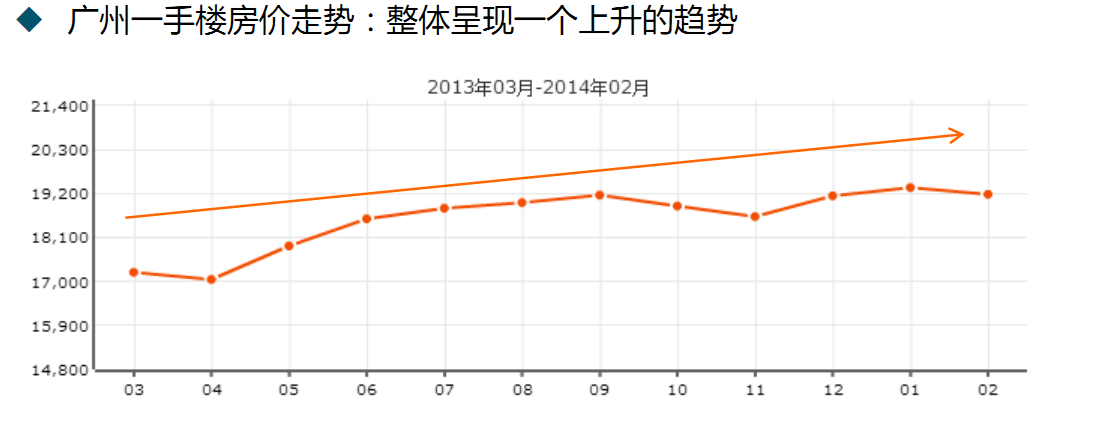
九、柱形图

　　显示一段时间内的数据变化或显示各项之间的比较情况。

　　

 

十、饼图

　　饼图（饼状图），根据各项所占百分比决定在饼图中的扇形面积，简单易懂，通俗明了，可以更加形象地看出各个项目所占的比例大小。

，可以更加形象地看出各个项目所占的比例大小。