4、快速排序

4、快速排序

　　4.1　分而治之

　　　　快速排序 —— 一种使用D&C（divide and conquer）的排序算法。

　　　　使用D&C解决问题的过程包括两个步骤：

　　　　（1）找出基线条件，这种条件必须尽可能简单。

　　　　（2）不断将问题分解（或者说缩小规模），直到符合基线条件。

　　　　代码清单4-1　求和

# -*- coding:UTF-8 -*-
# 使用循环求和
def sum(arr):
    total = 0
    for x in arr:
        total += x
    return total

# 使用递归求和
def sum2(arr2):
    if arr2 ==[]:
        return 0
    return arr2[0]+sum(arr2[1:])


print sum([2, 4, 6])
print sum2([2, 4, 6])

　　　　4.2　快速排序

　　　　快速排序是一种常用的排序算法，比选择排序快的多。快速排序也使用了D&C。

　　　　归纳证明是一种证明算法行之有效的方式，它分两步：基线条件和归纳条件。

　　　　快速排序是最快的排序算法之一，也是D&C典范。

　　　　代码清单4-2　快速排序　　

# -*- coding:UTF-8 -*-
# 快速排序


def quicksort(array):
    # 基线条件：为空或只包含一个元素的数组是“有序”的
    if len(array) < 2:
        return array
    # 递归条件
    else:
        pivot = array[0]
    # 由所有小于基准值的元素组成的子数组
    less = [i for i in array[1:] if i <= pivot]
    # 由所有大于基准值的元素组成的子数组
    greater = [i for i in array[1:] if i > pivot]
    return quicksort(less) + [pivot] + quicksort(greater)


print quicksort([10, 5, 2, 3])
# result: [2, 3, 5, 10]

 

　　　　4.3　合并排序

　　合并排序（merge sort），运行时间为，比选择排序快得多，最糟情况运行时间为。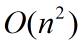

 　　大O表示法中的常量有时候事关重大，这就是快速排序比合并排序快的原因。