Madoka and The Best University (cf E)( 枚举一个其中一个元素,欧拉函数,gcd)

#include<iostream>
#include<cstring>
using namespace std;
const int Maxn=1e7;
int phi[Maxn];//记录数的约数个数(欧拉函数) 
bool vis[Maxn];//记录数字是否访问 
int prime[Maxn];//保存素数 
int main()
{
    memset(vis,false,sizeof(vis));
    memset(phi,0,sizeof(phi));
    memset(prime,0,sizeof(prime));
    int n;
    scanf("%d",&n);
    vis[1]=1;//1不是素数 
    for(int i=2;i<=n;i++)
    {
        if(!vis[i])//没有被访问，也就是没有被筛掉,说明是素数 
        {
            vis[i]=!vis[i];
            prime[++prime[0]]=i;
            phi[i]=i-1;
        }
        for(int j=1;j<=prime[0]&&i*prime[j]<=n;j++)
        {
            vis[i*prime[j]]=true;
            if(i%prime[j]==0)//a%b==0，那么phi[a*b]=b*phi[a] 
            {
                phi[i*prime[j]]=phi[i]*prime[j];
                break;
            }
            else phi[i*prime[j]]=phi[i]*(prime[j]-1);//两者互素 
        }
    }
    printf("%d\n",prime[0]);
    for(int i=1;i<=prime[0];i++)
    {
        printf("%d %d\n",prime[i],phi[prime[i]]);
    }
    return 0;
}

欧拉函数(详细证明+推导) 每日一遍，算法再见！_欧拉函数推导_鲜果维他命的博客-CSDN博客

 

 思路:

• a+b 是gcd(a,b)的 倍数, 利用调和级数 
• 然后 gcd 化简 

  

•  

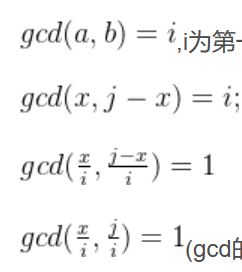
  根据此式子可知,x的取值的方案数就是和(j/i)互质并且比它小的数的个数.这就是欧拉函数的定义,那么a,b的取法就有phi[j/i]种.