高数--积分

不顶积分定义：对一个函数 求他 其中一个原函数 ++++++++++++++++++++++++++ccccccccccccccccc

 

积分变量很重要

 

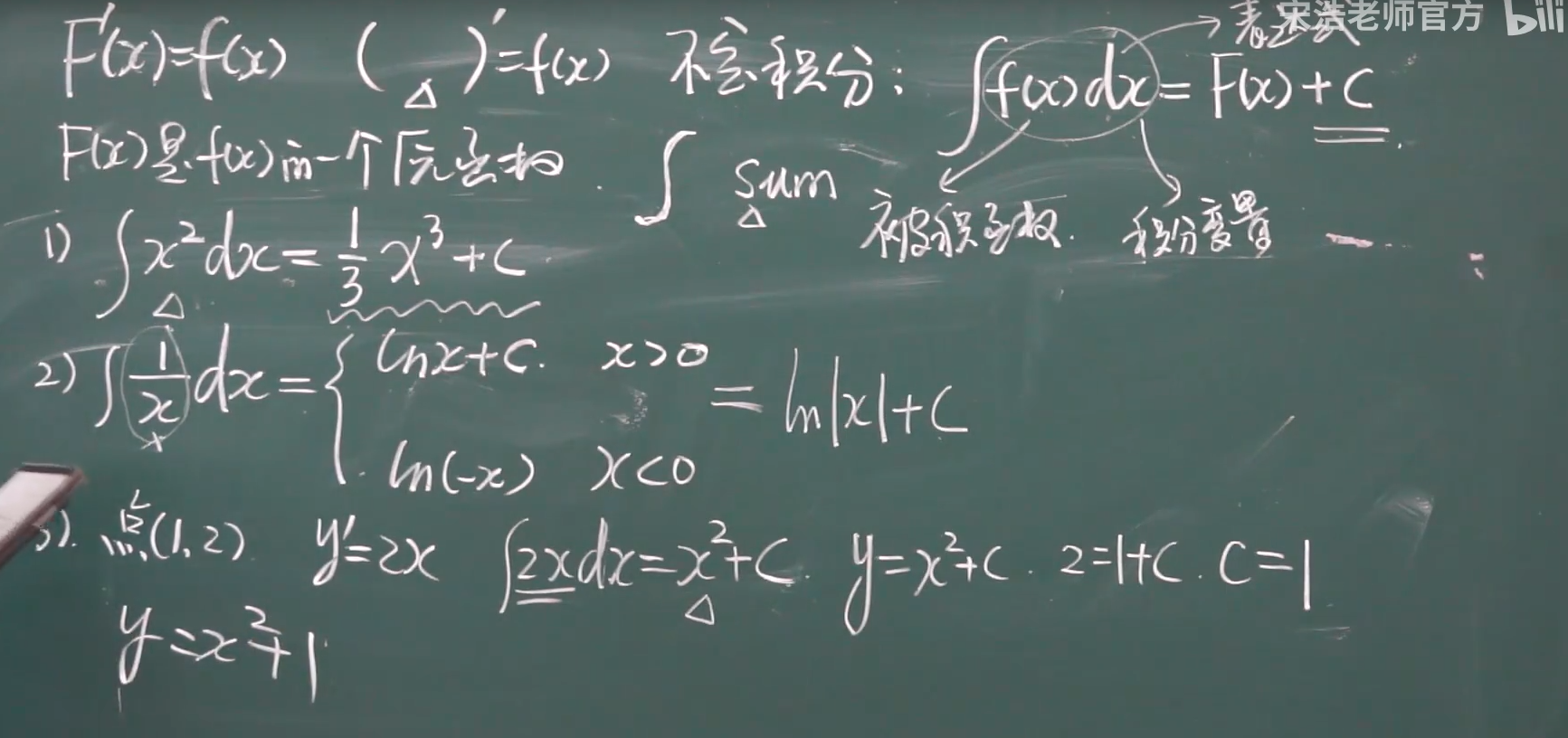
图像定义： 平行的图像簇

小公式定义：

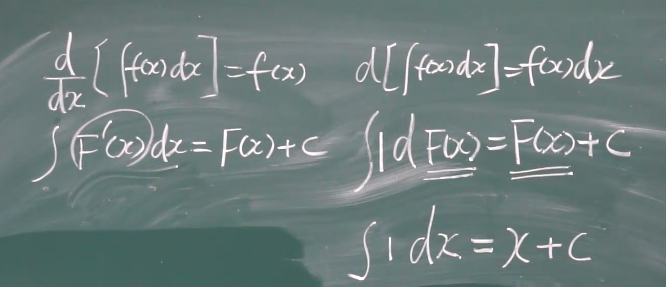
积分表：

记住ln那个 其他的，可以反推

 

 

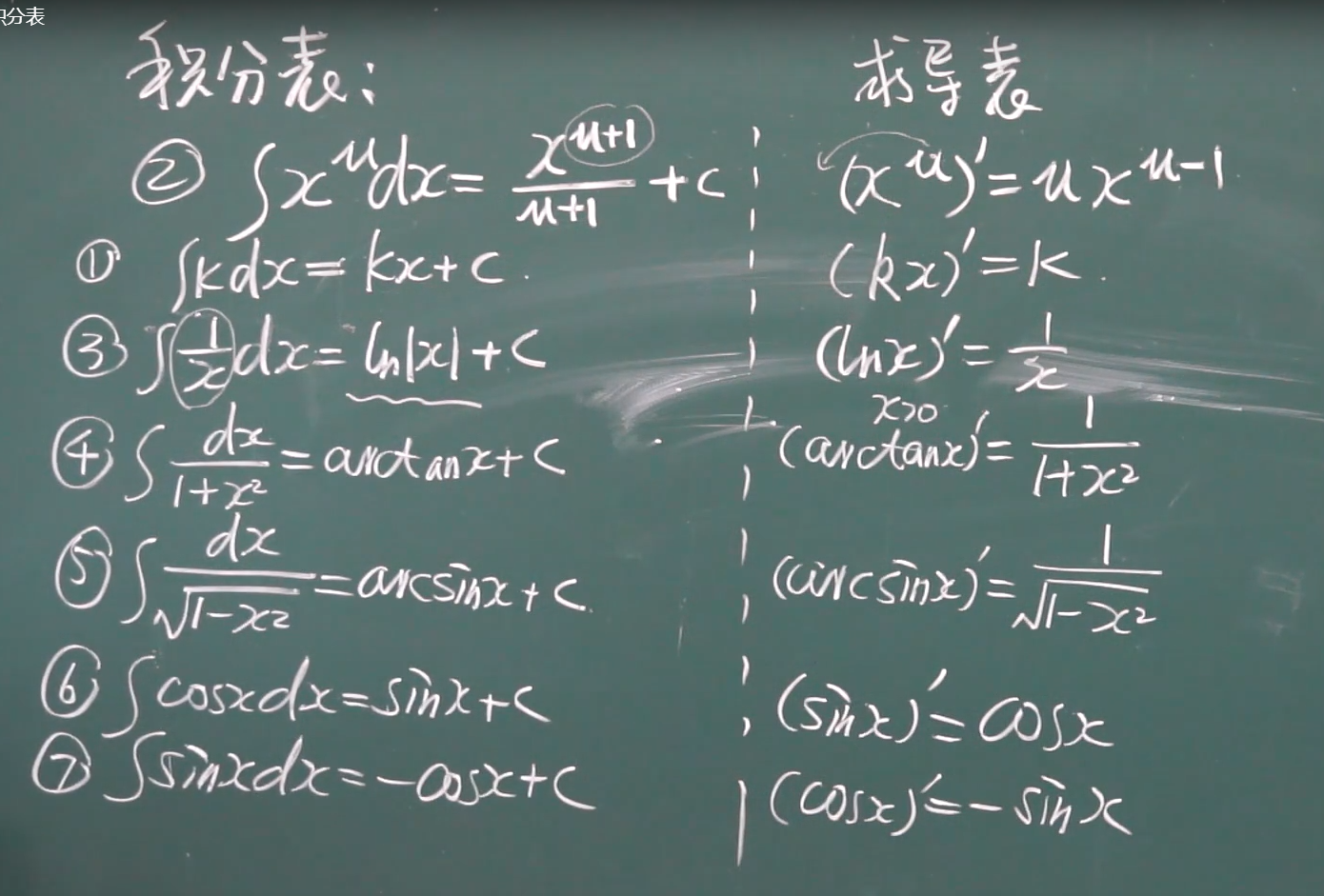
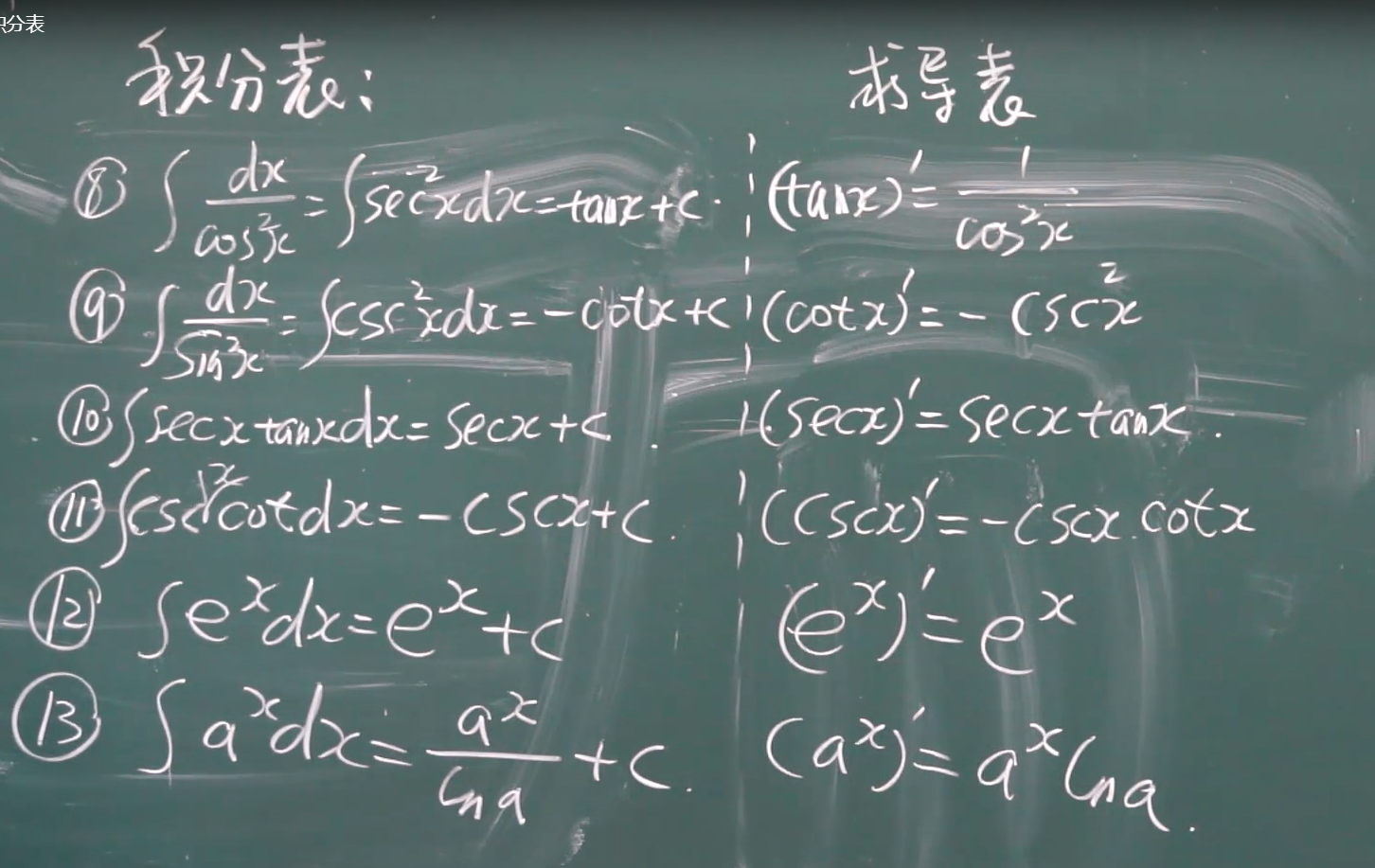
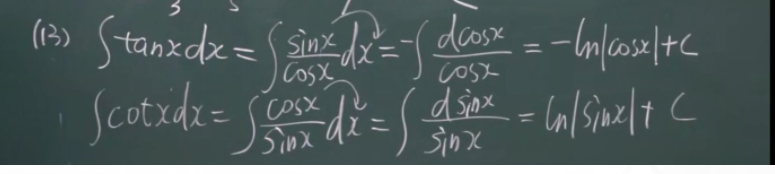
余割的原函数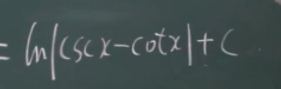：   正割的原函数 ln|secx+tanx|+C

 

 

对于 三角函数 倒下去的 sin^2 or cos^2 就积分表可用 对于正着的  sin^2 cos^2 可以利用二倍角公式 sin 和 cos 就积分表 tan^2就直接用 sec^2-1; 

不定积分性质： x/ 不分开  

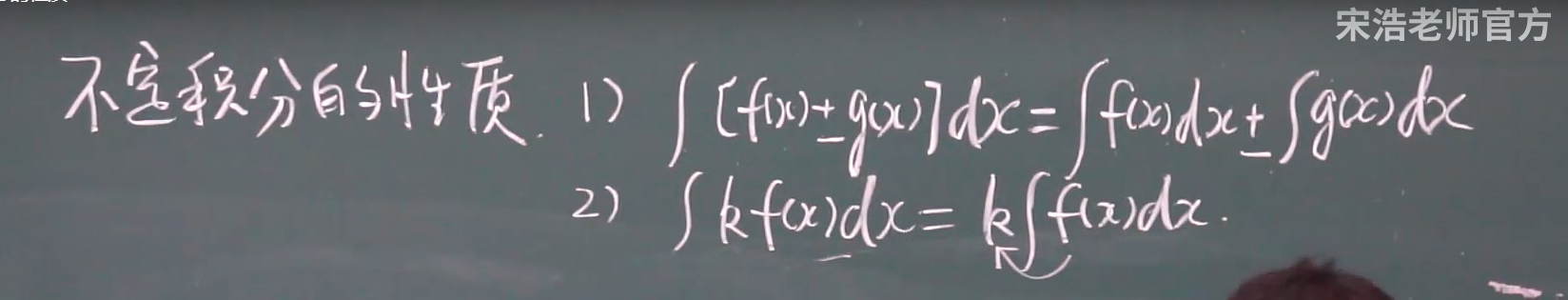
做题只能用积分表公式+形式，没有就化形式， 三角函数利用 二倍角公式

例题：很重要，每一道题都要看

分式除法（也可以用消的思想）

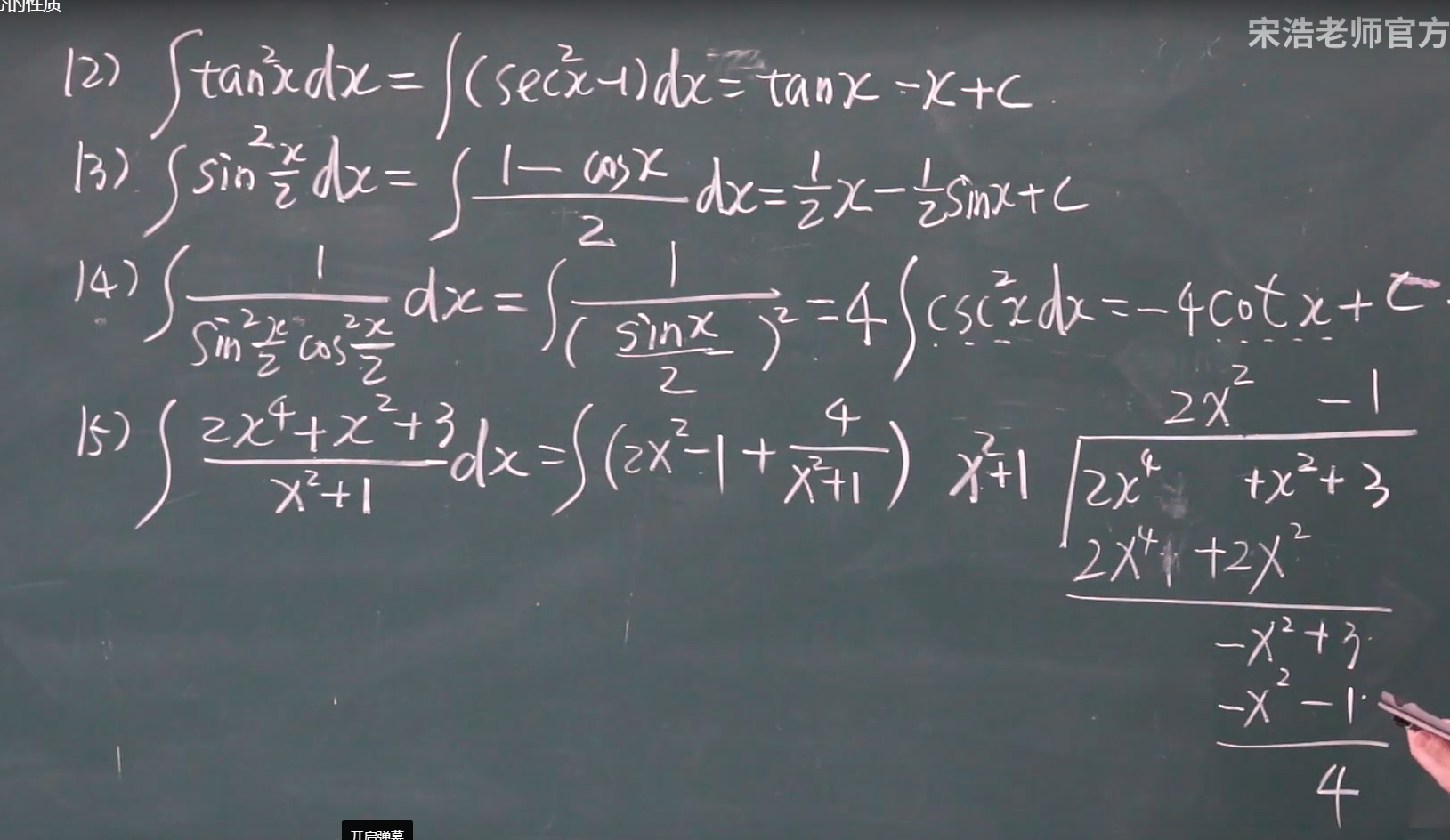
第一换元积分法 

核心： 用凑的思想 把d 前面的内容换到 d 后面去。

运算： d的系数根据需要随便改 可以随便加常熟项；系数拿进来拿出去都可以；

           里面和外面的次数相等时，就随便凑，不相等，就要想积分表，看那个相似

栗子 很重要 每一个都要仔细看：

注意： 在拿出去的时候， 还原的东西的系数 很重要 ，在导一下，看符不符合。 

 +++++cccccccccccccccc ++++c +c+c+c+c+c+c+c+c+c+c+c+c+c+c+c+c+c+c+c+c+c+c+c+c+c+c+c+c+c+c+c+c+c+c+c+c+c+c+c+c+c+c+c+c+c+c+c+c+c+c+c+c+c+c+c+c+c+c+c+c+c

 

 

 

 

 

 

 

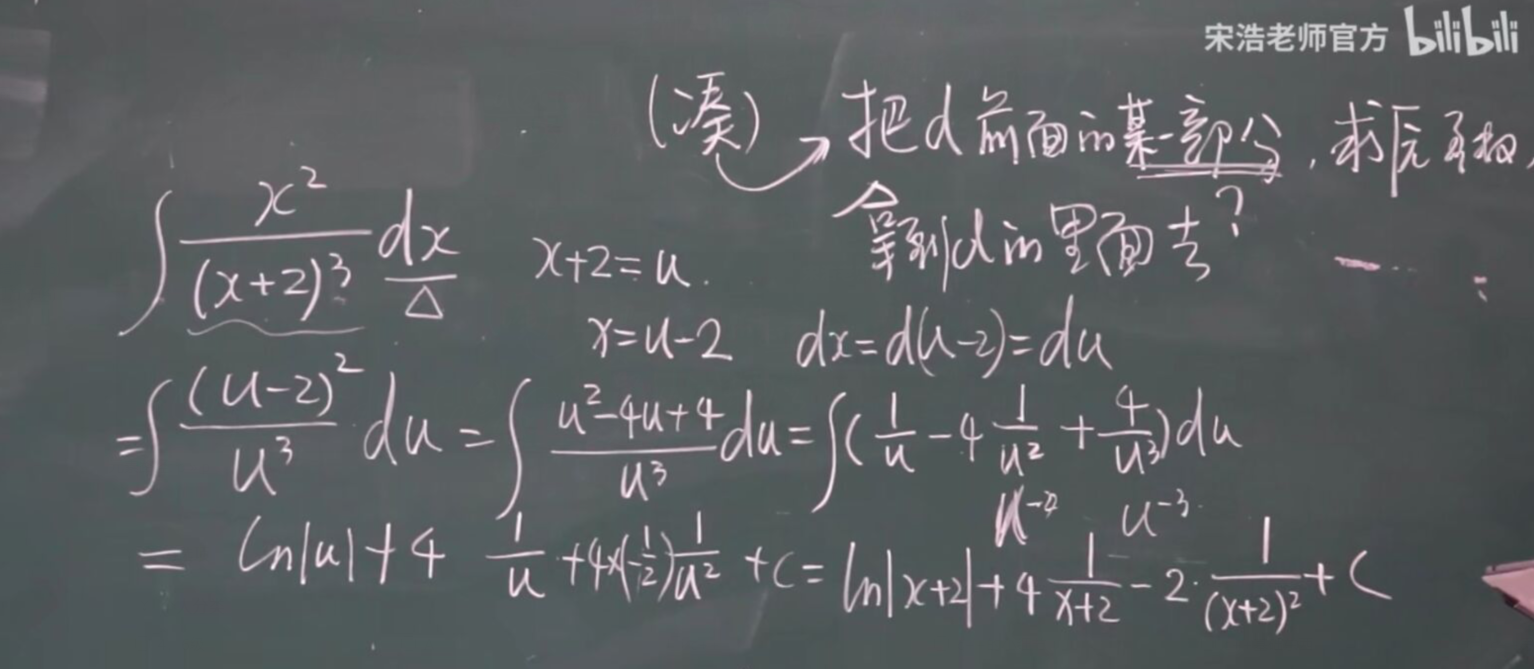
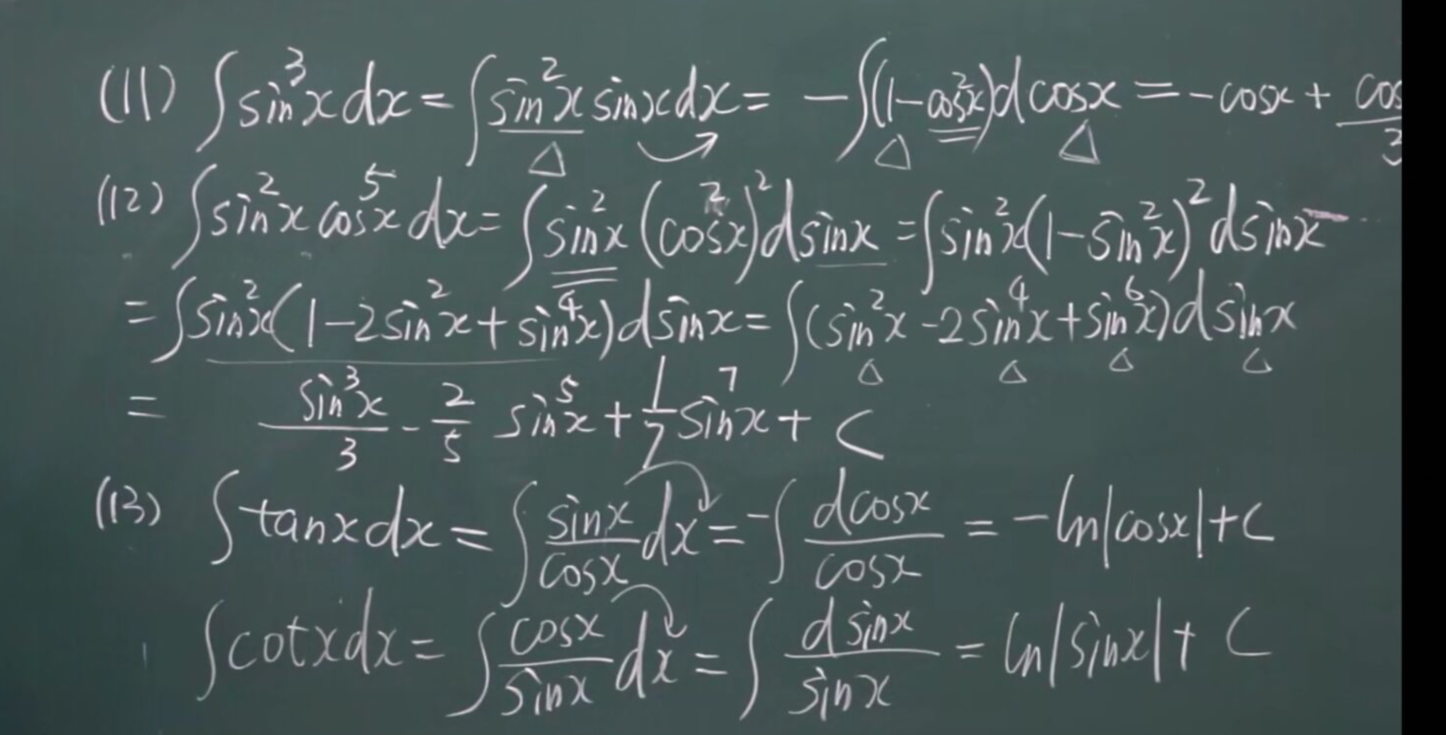
结论 ： yuge csc 的原函数  ln 的 lyuge - yuqie l + C

三角函数 ： 1+ tan的平方= sec的平方

小公式，其他同理推；

 

 

第二换元积分法

核心： 通过换元（多用3角函数）去凑一个平方 把根号去掉；

            换元后 最后要把他给换回去

栗子，很重要，每一个都要看；

注意：反函数的使用 arc

 

 

分部积分法

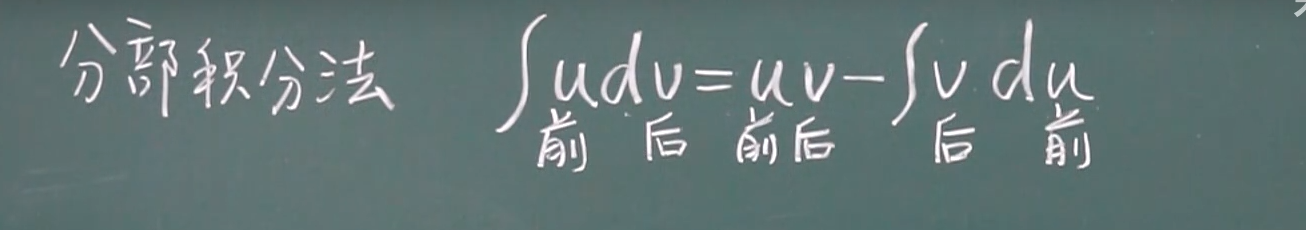
技巧+例题+常用公式

 

 

 

 

 

 

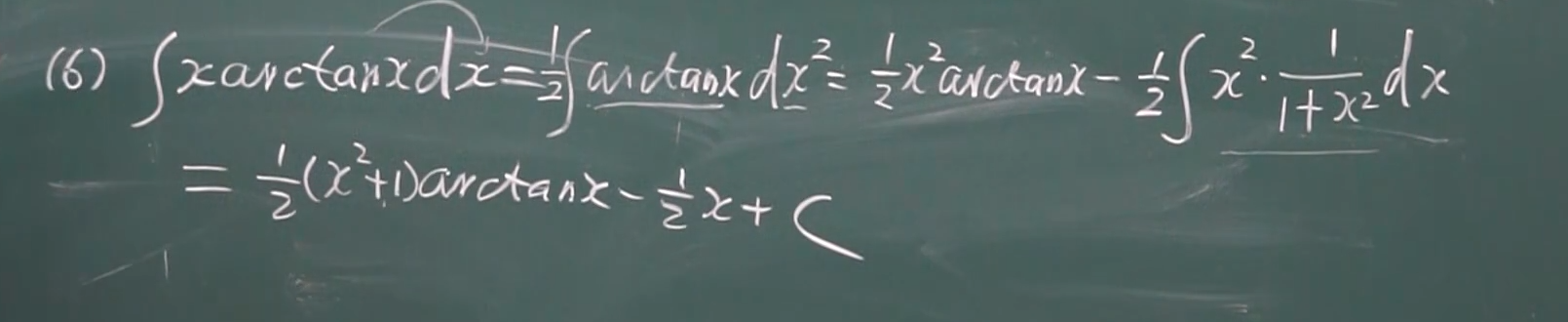
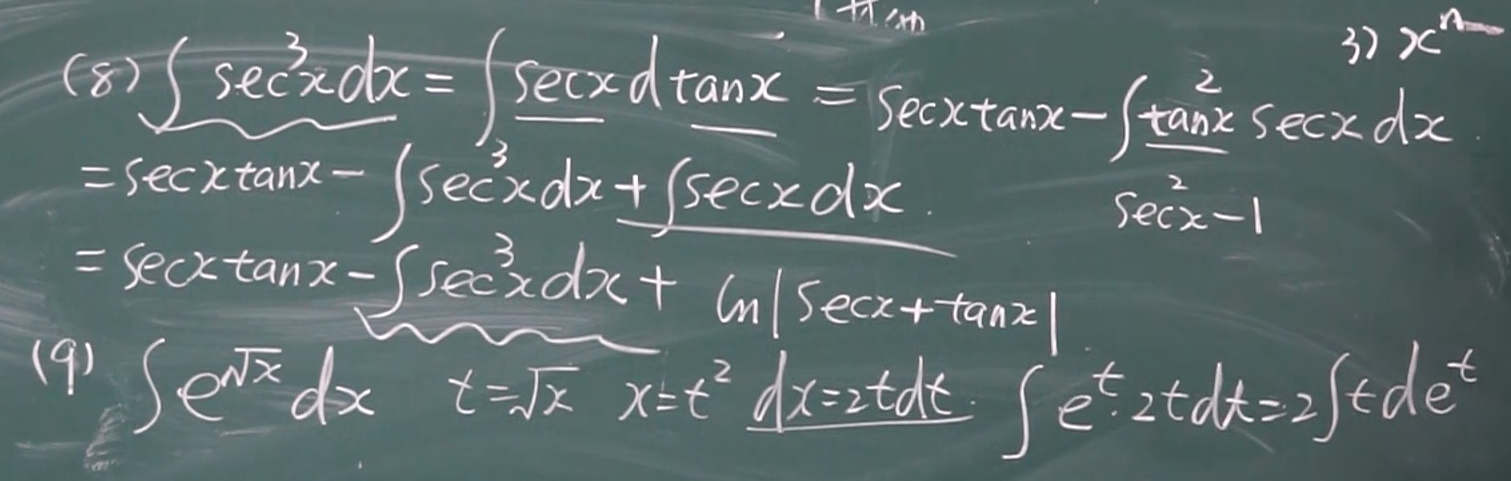
有理积分

小点：1 注意arctanx 的 导数 形式 2 分式可以利用加法性质拆分成2个。

 

 

 

 

 

 

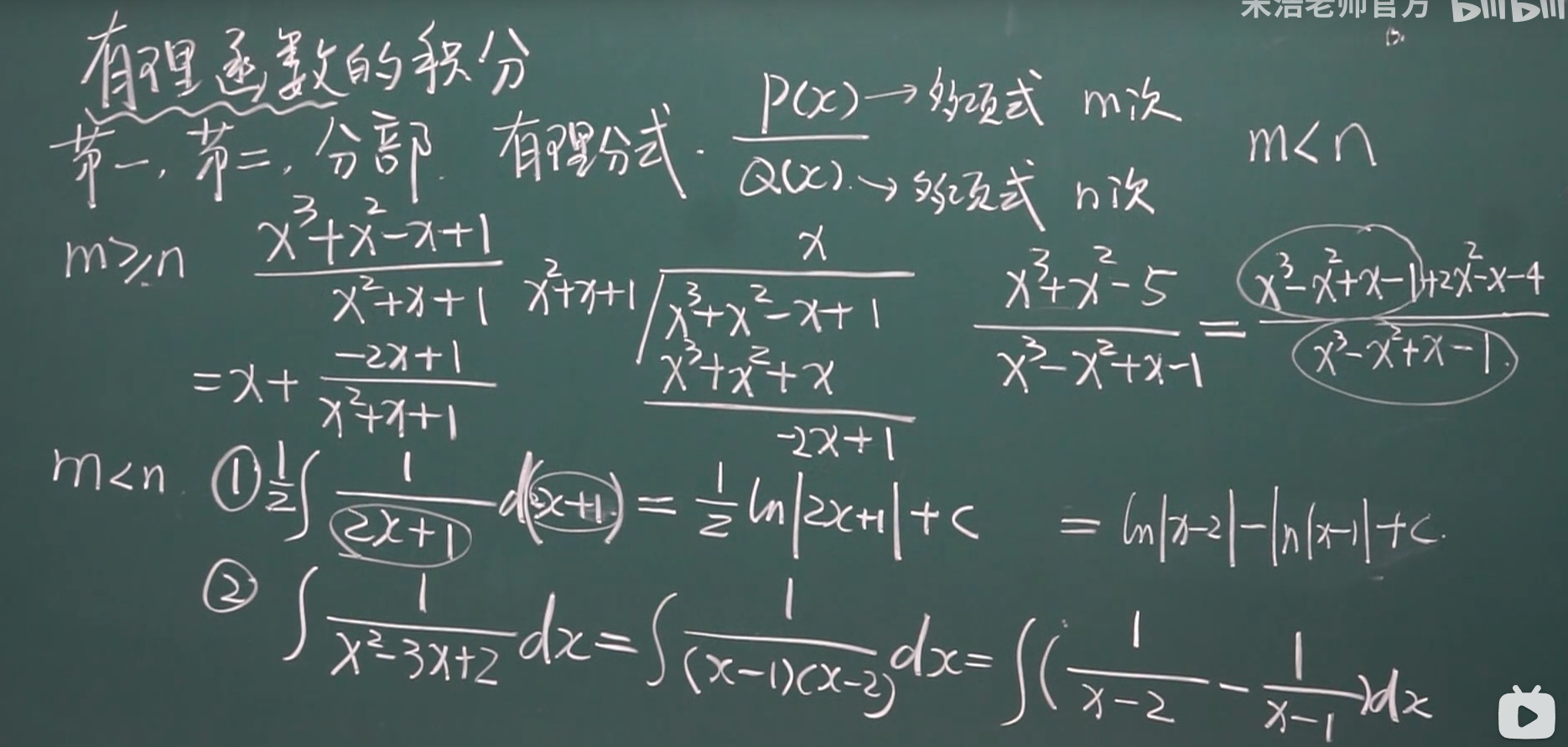
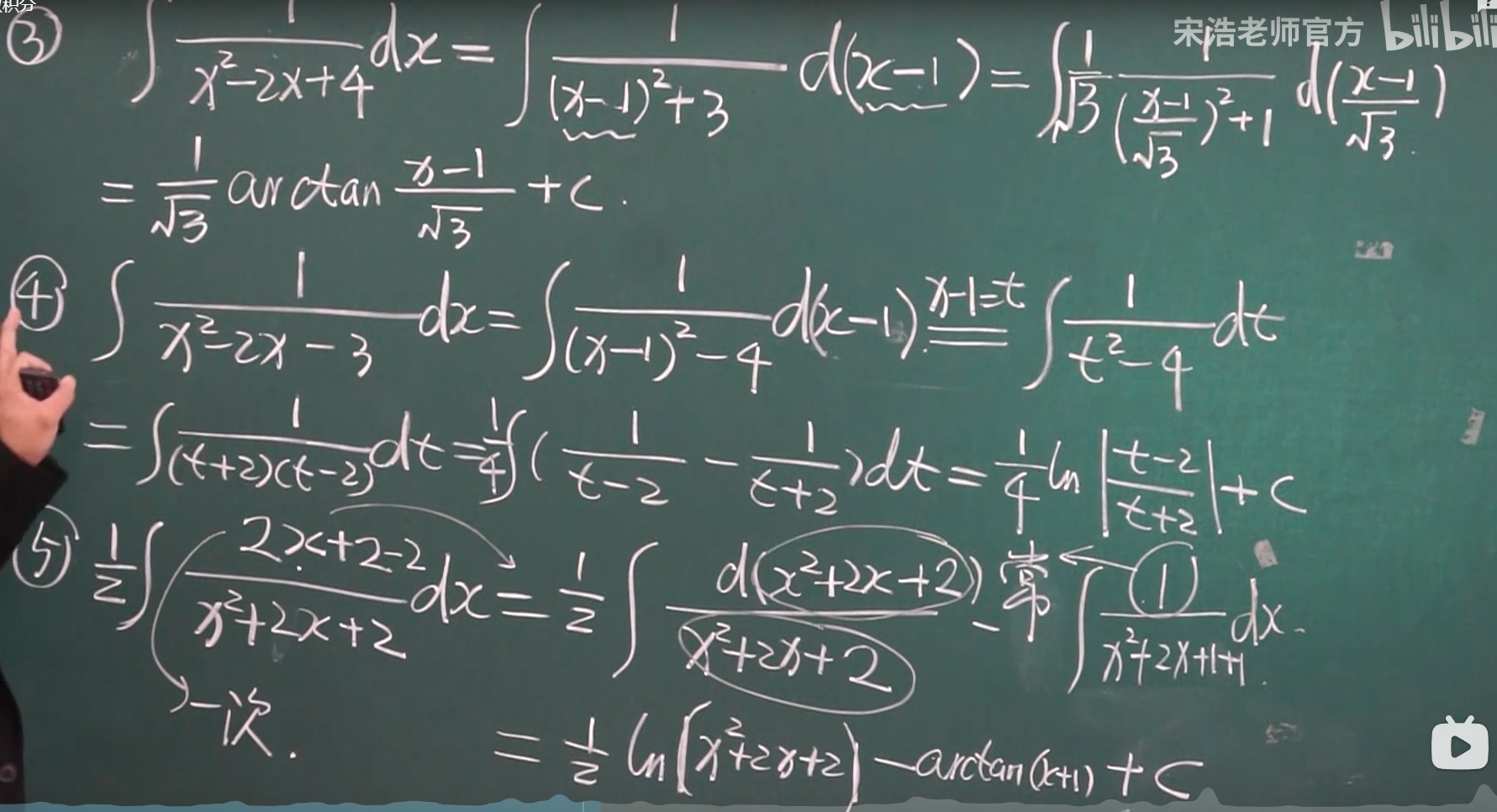
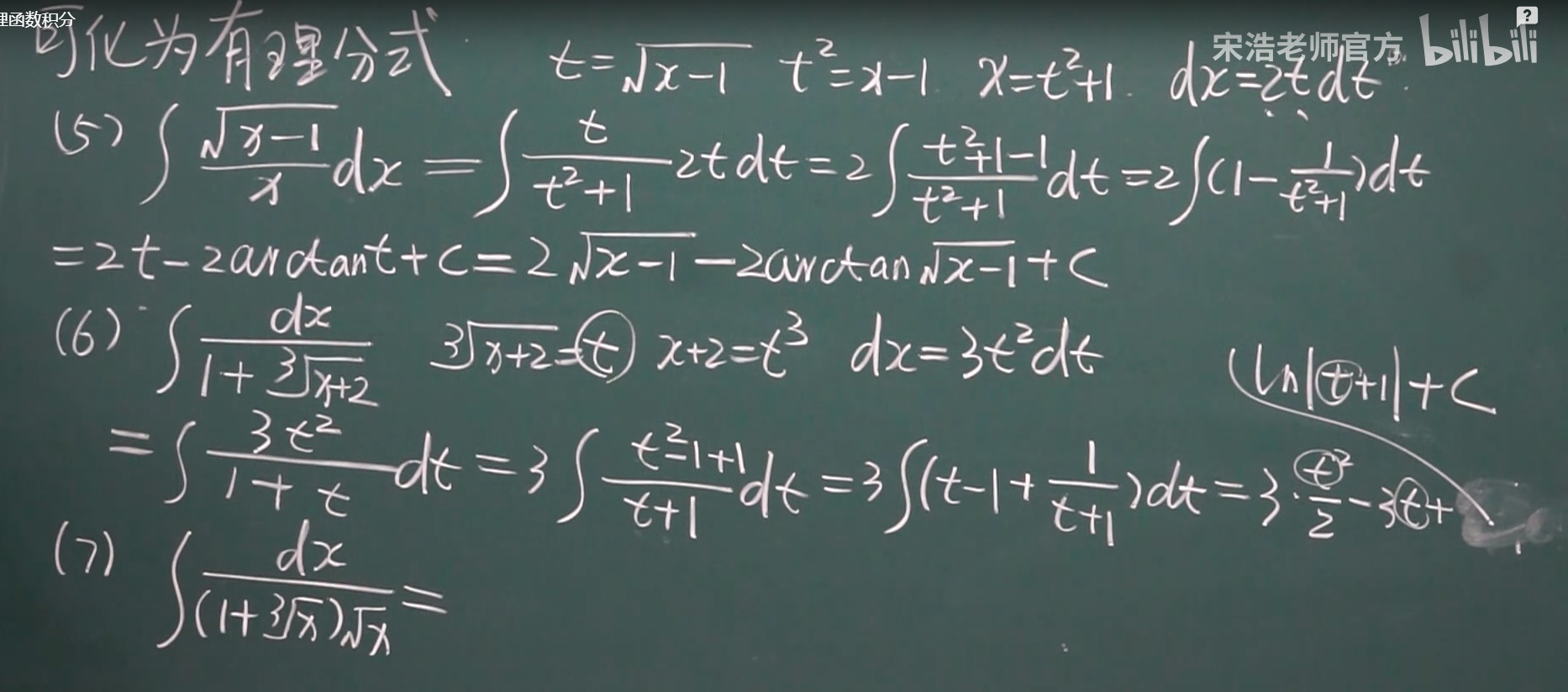
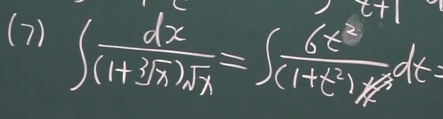
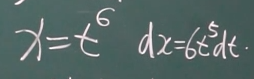
定积分：

导入：

就是求f（x）的原函数 他的原函数的性质相加的起来就好比 面积

 

 

栗子

 

 

 

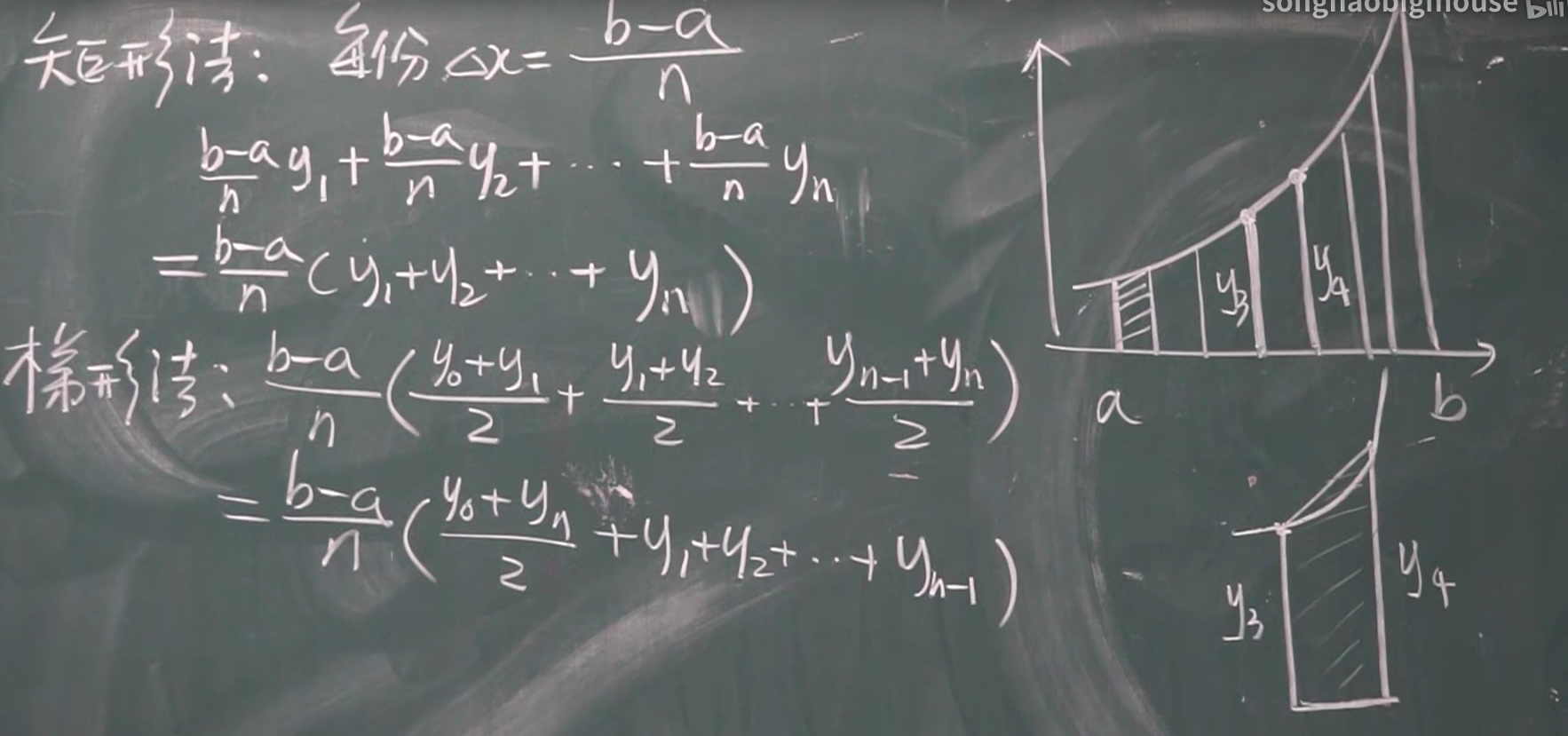
还有一种抛物线的思想

 

 

 

重要性质：

微积分基本公式：

 

 

 

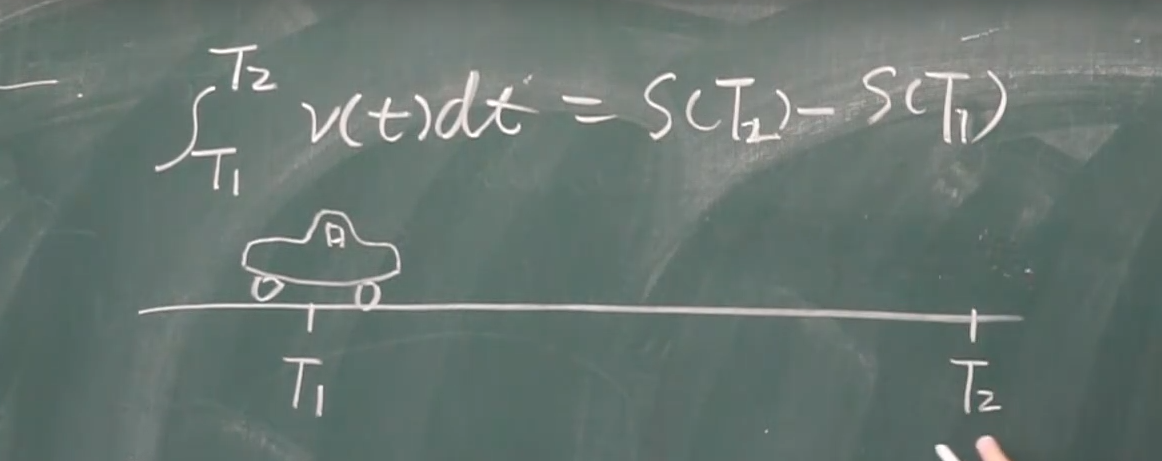
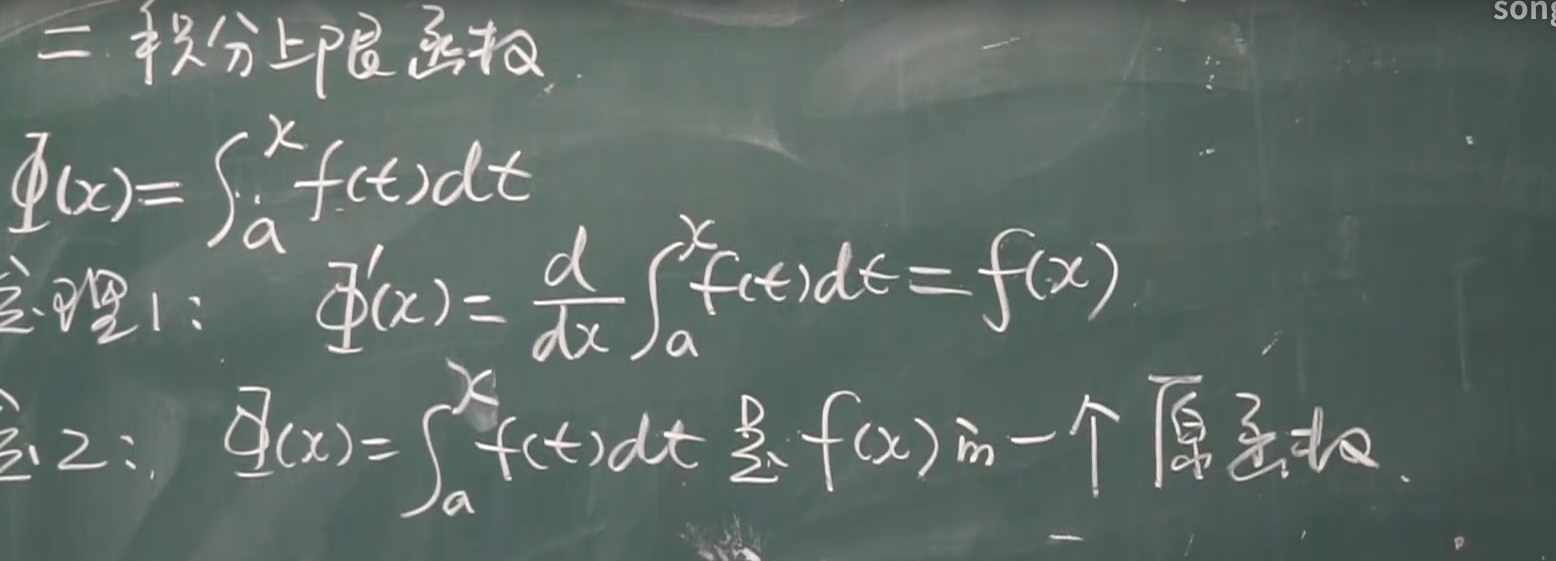
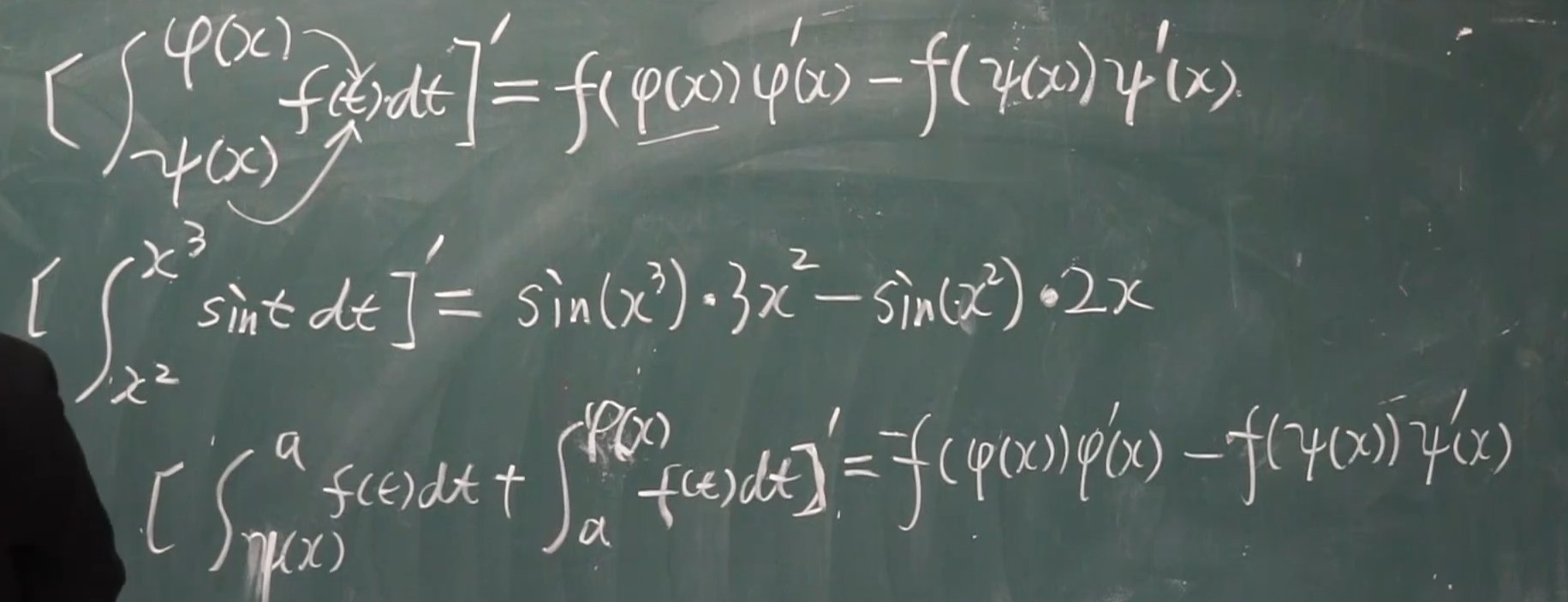
栗子：

 

 

 

 

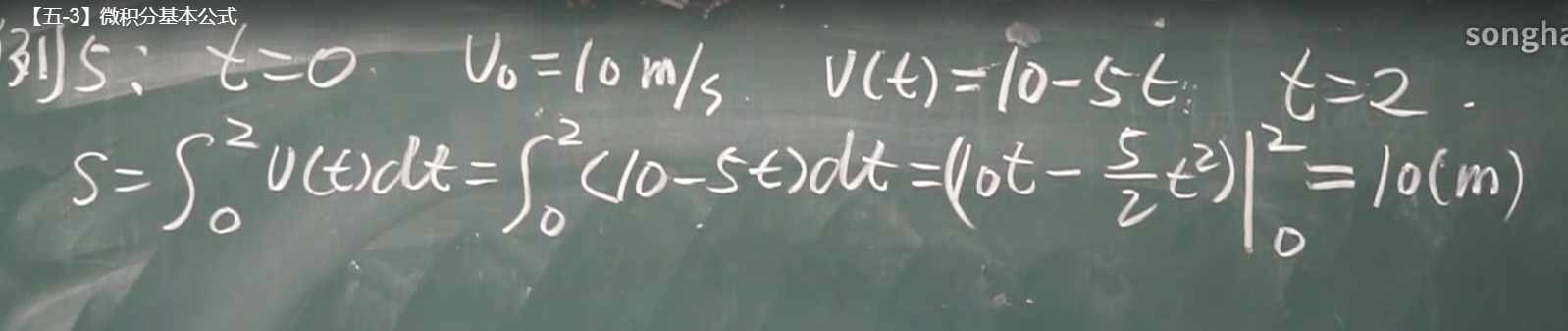
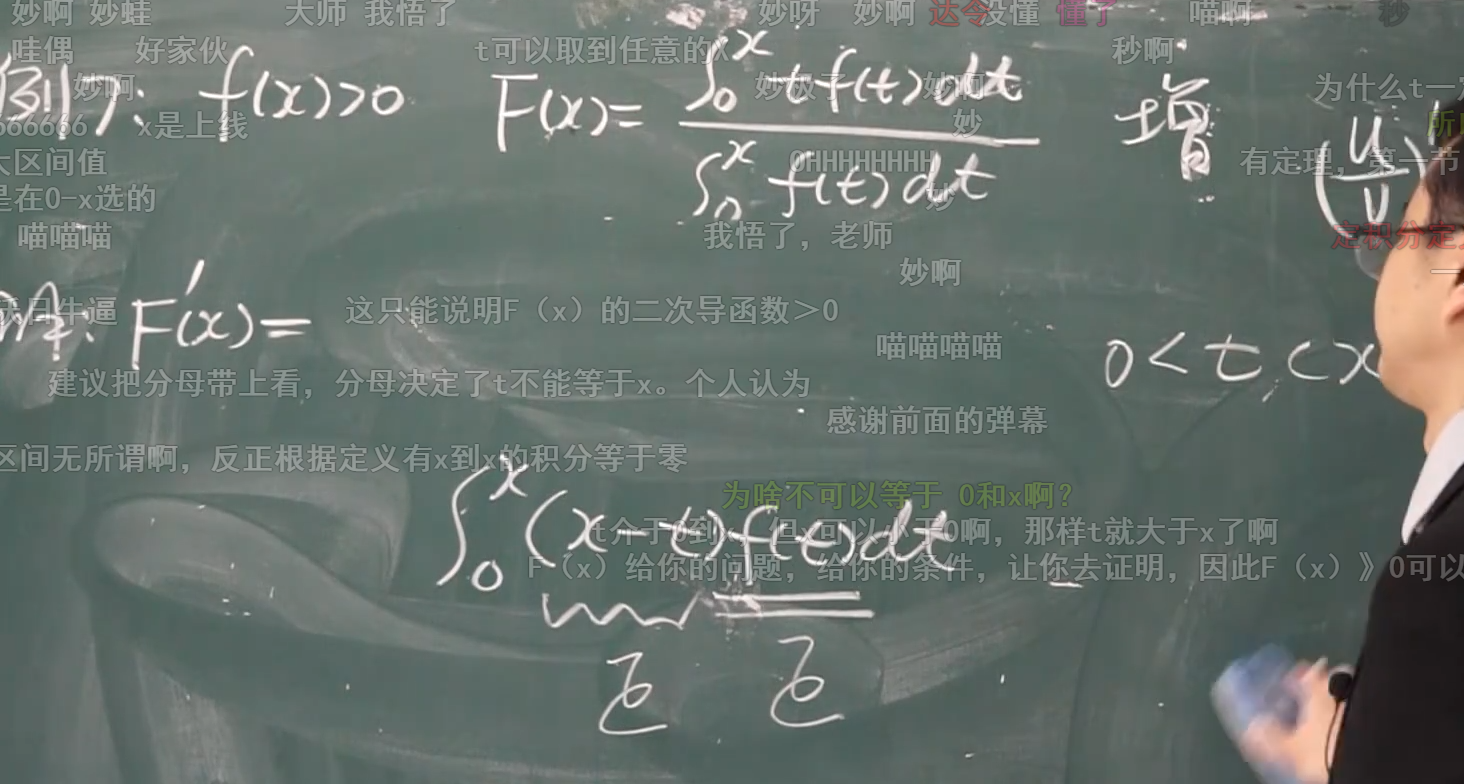
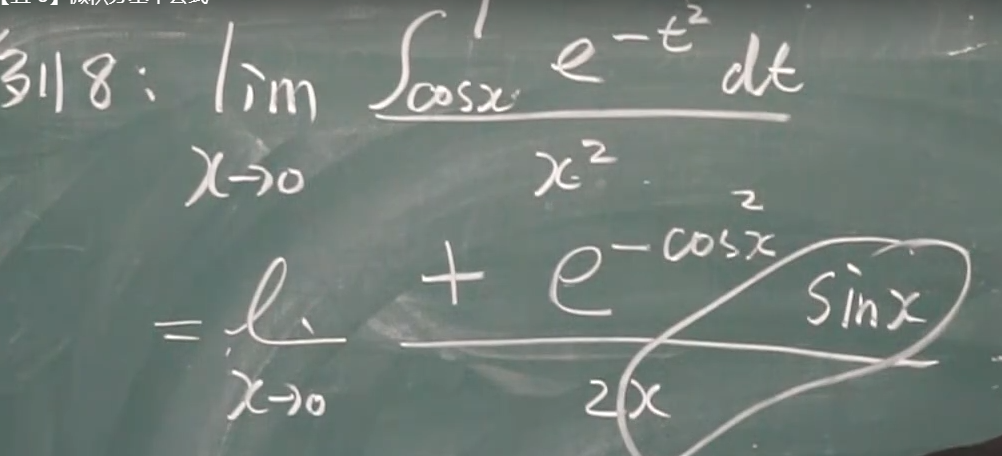
定积分----换元

 

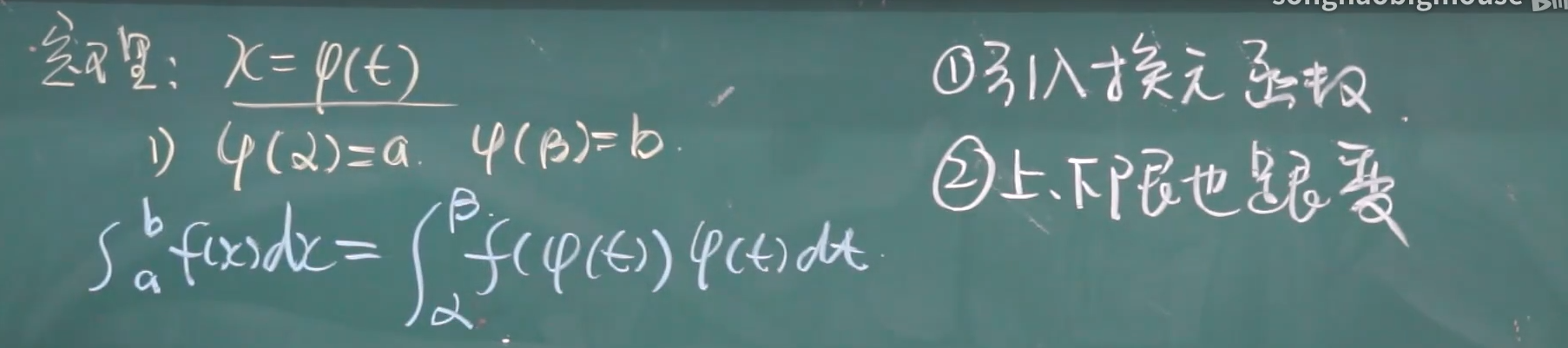
 例题 注意看格式

 

 

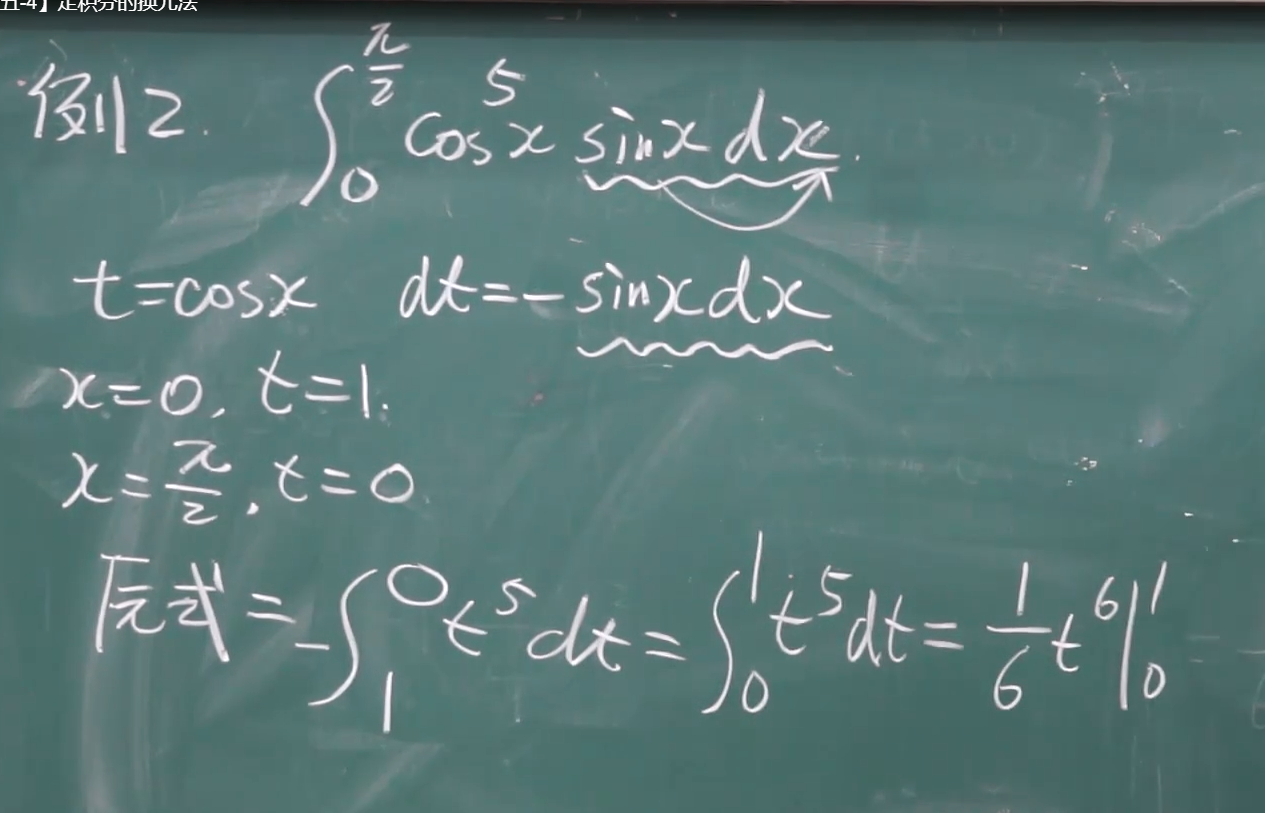
 下面这个知识点很关键： 在求定积分时，分开看的时候一定要看他是不是奇函数 直接 就口语给他消掉；

 

 

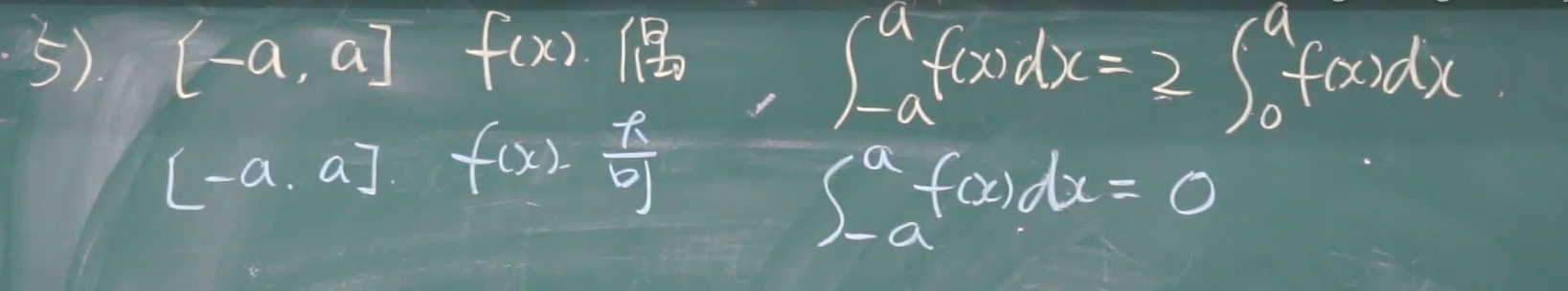
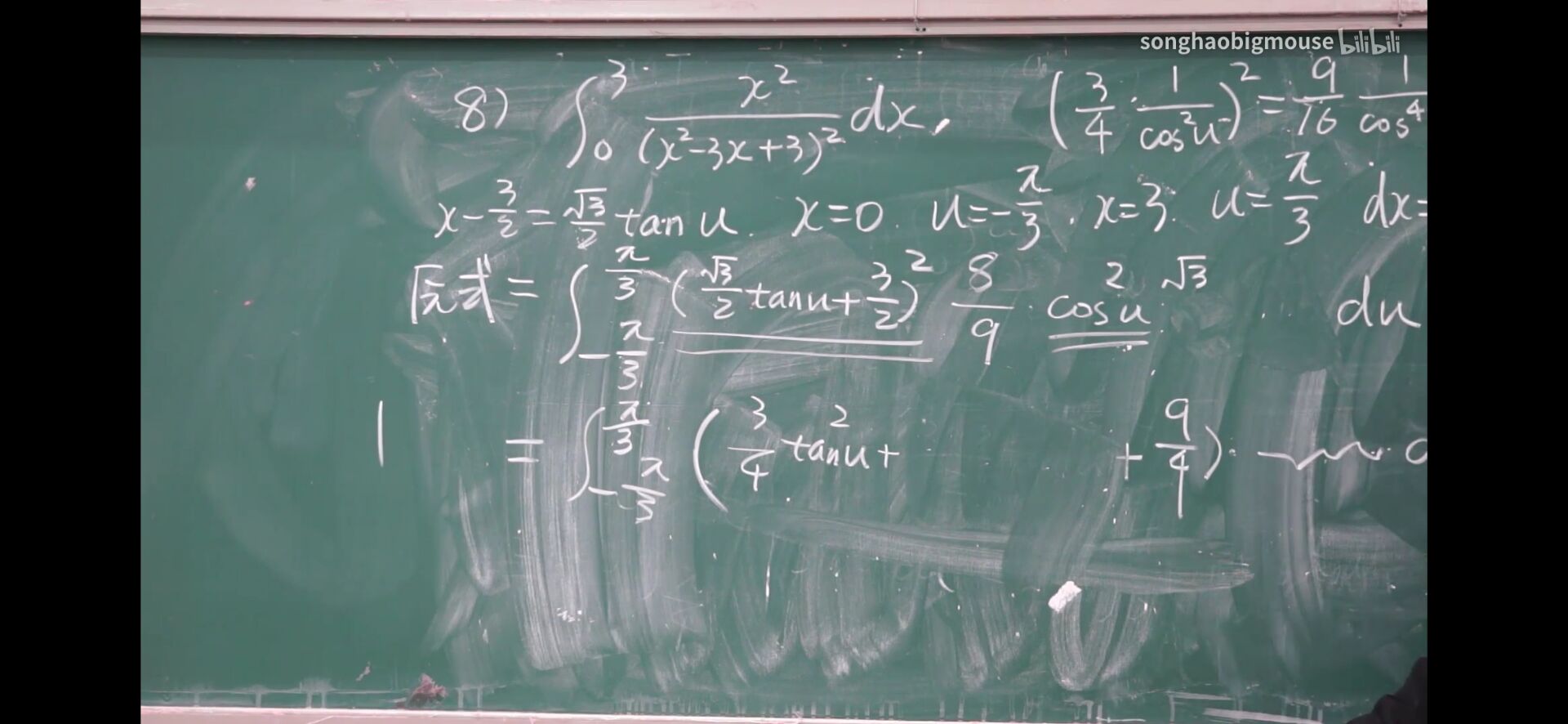
很关键的地方：一定要看清对那个地方求积分

 

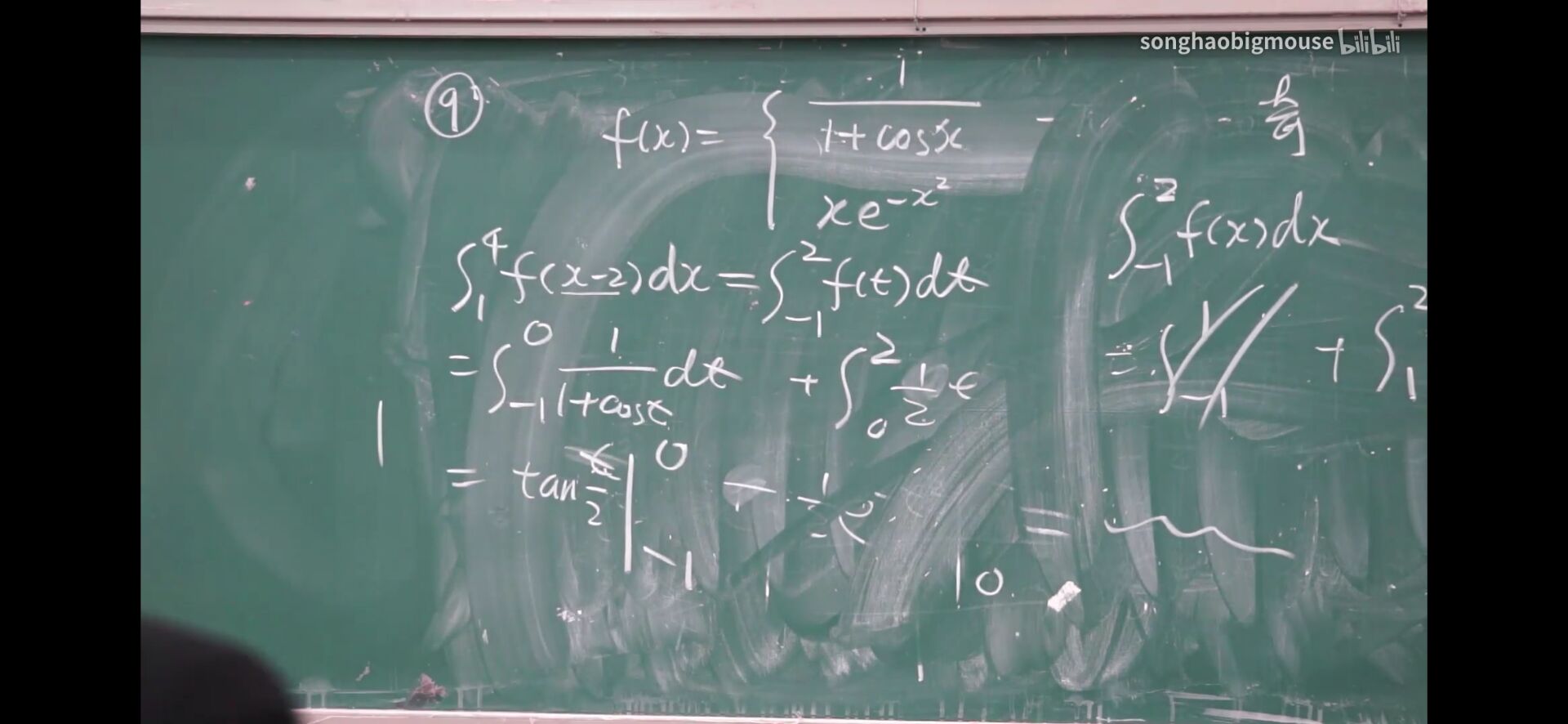
定积分的分部积分

 

 

 

 

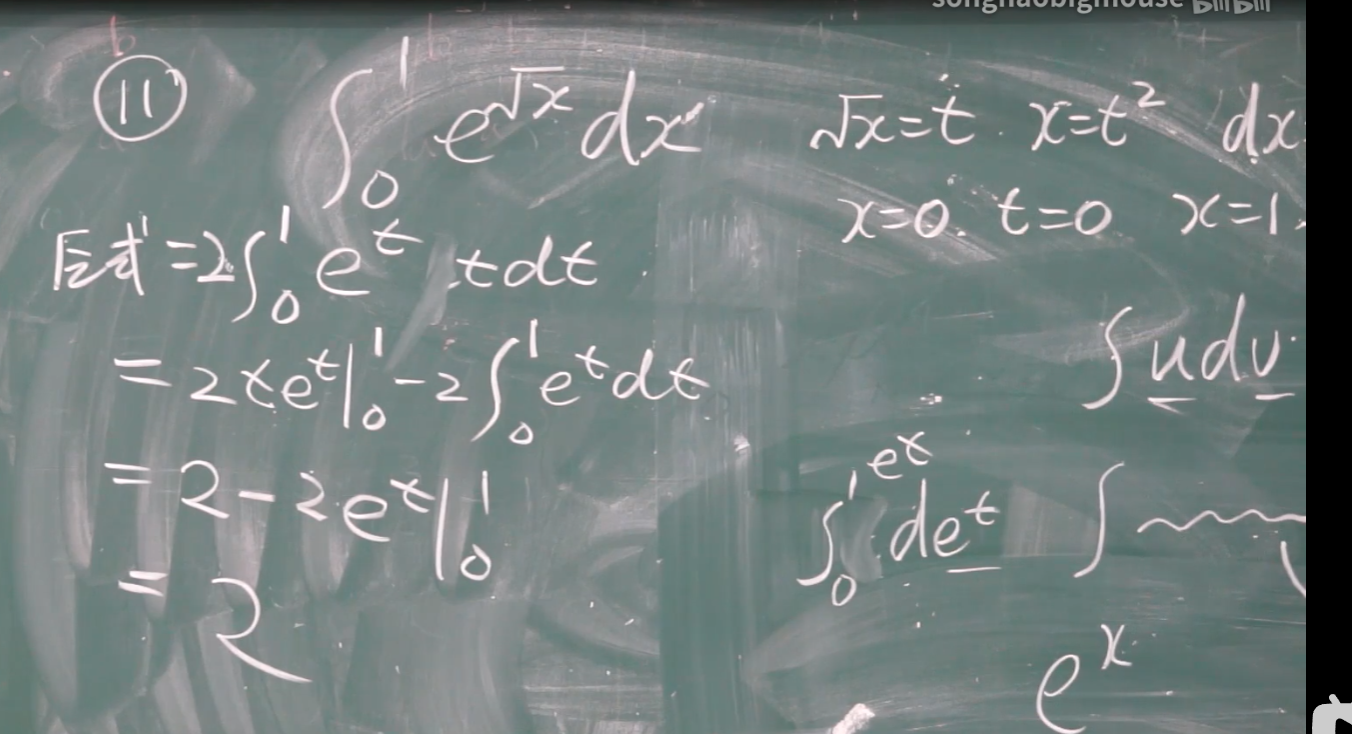
反常积分：

 

 

 

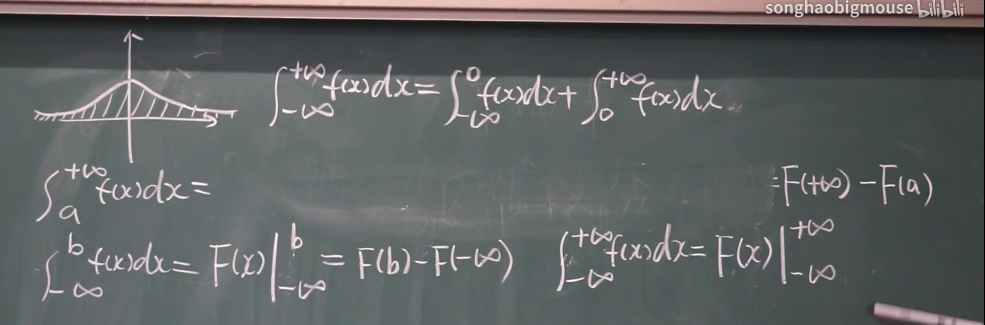
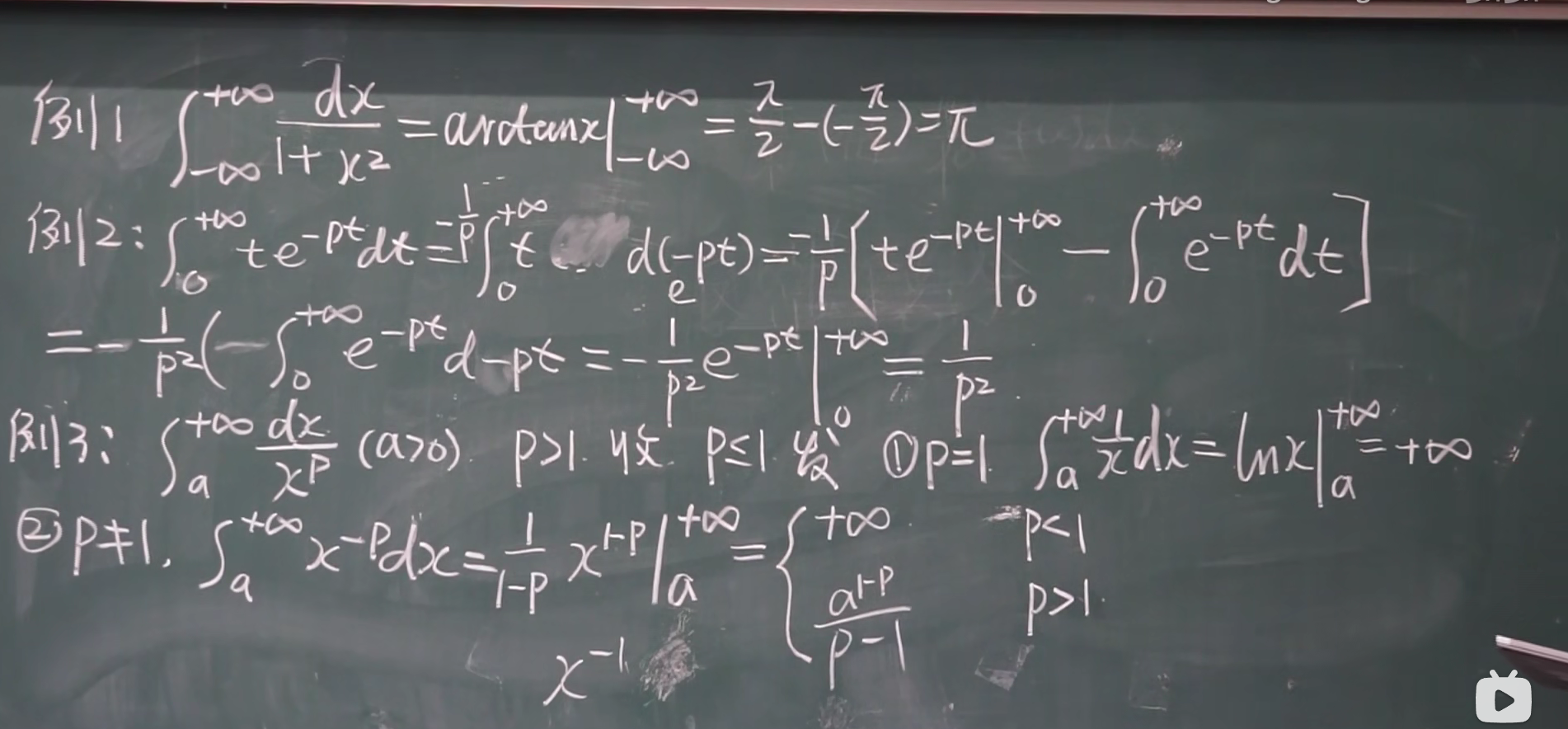
 无解反常函数：

 

 

 

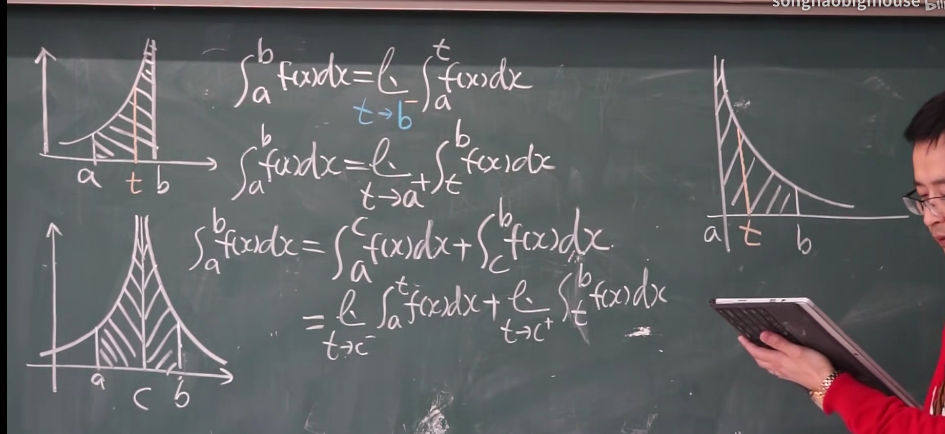
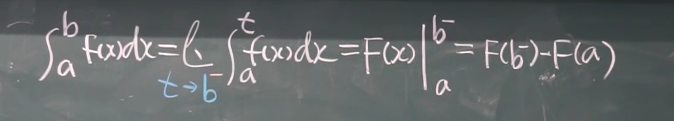
栗子：

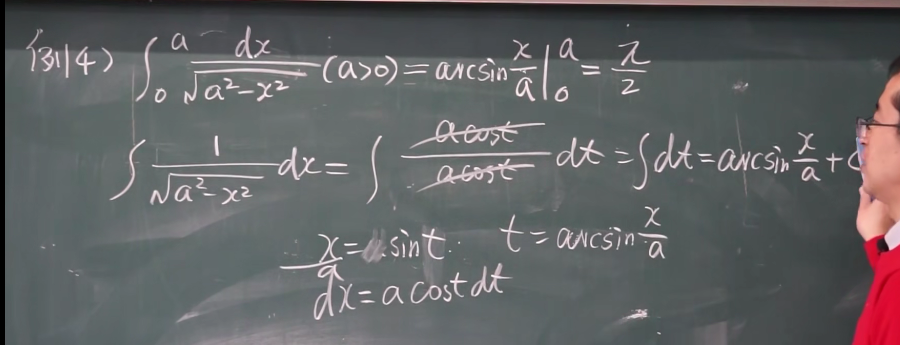
注意欺骗性 定义域特别注意；

无界反常函数： 特别注意 换元时 要是一个单调的函数

 

伽马函数：