LES大涡模拟-【转载】第一部分 Eddies(涡)的解析

第一部分 Eddies(涡)的解析

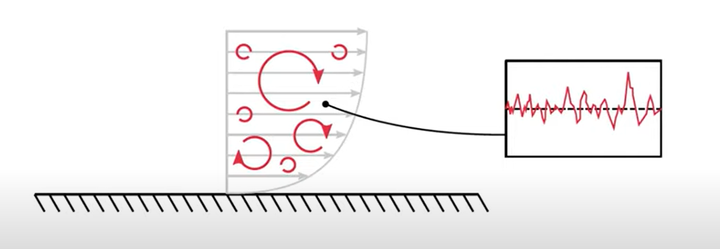
湍流流动中包含了许多的涡，他们所包含的能量、他们的大小都各异。

image

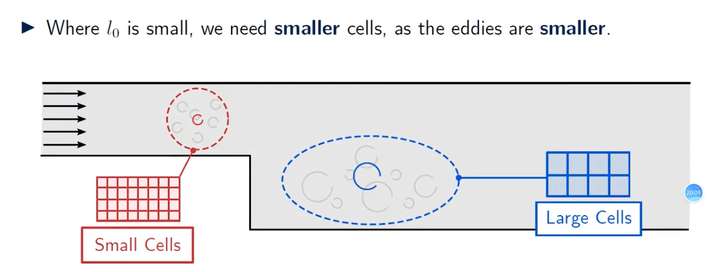
在LES中，我们需要在计算网格中解析这些涡中的一部分。

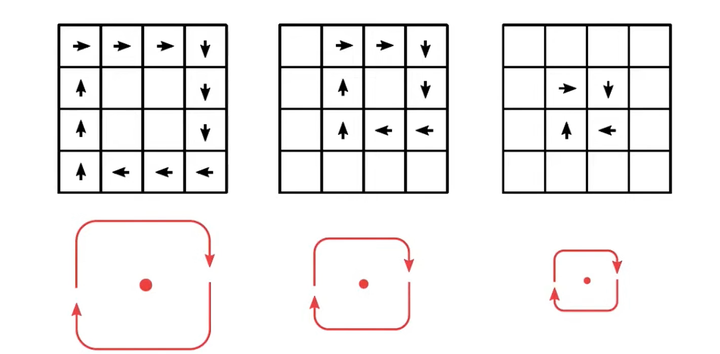
如何做到这件事？首先我们需要考虑的是怎么在一个CFD网格中解析一个涡。事实上，解析一个涡，我们至少需要一个 $2\times 2$ 的网格，也就是说，尺寸小于两个网格的涡就不能被解析出来，只能套用模型来表示它，这个模型也就叫做亚格子模型，这部分的内容之后再说。

image

所以现在我们知道，网格的尺寸确定了能够解析的最小的涡的大小，那么如何确定一个合理的网格尺寸来保证流场的准确性呢？在算一个LES算例之前我们要怎么确定LES的网格尺寸？

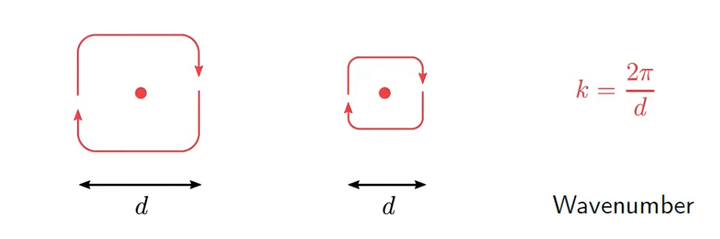
波数k

波数(k)是涡(Eddy)的空间频率

image

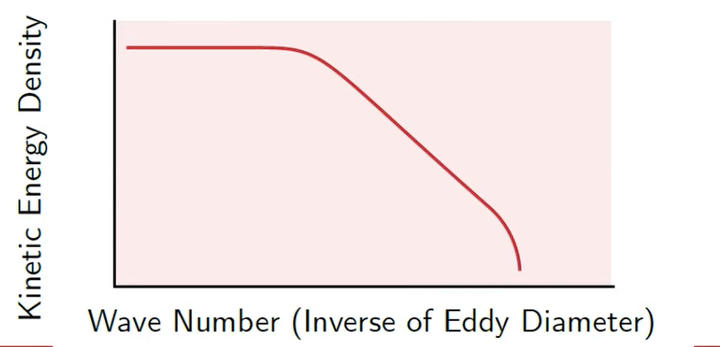
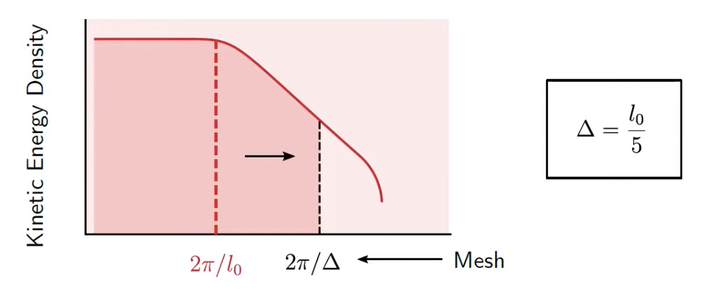
根据定义我们知道，越小的涡波数越大。这时候我们就需要知道一个东西，叫做湍流能谱。它的实验测量结果如下：

image

这张图说明，随着涡的波数的增大(/尺寸的减小),其湍动能密度逐渐减小。

对这张图沿着曲线积分，最后可以得到湍流动能。

在LES的网格设置中，并不需要解析所有的涡，因为涡越小，需要的网格越小，网格量就会越多，最后导致计算开销过大。怎么选择一个合适的网格尺寸，在保证我们认为的精度足够的条件下，还能尽量的减少网格量。一般认为一个好的LES算例，其网格的尺寸至少要小到能够解析80%的湍动能，而剩下部分的湍动能则是通过亚格子模型给出。

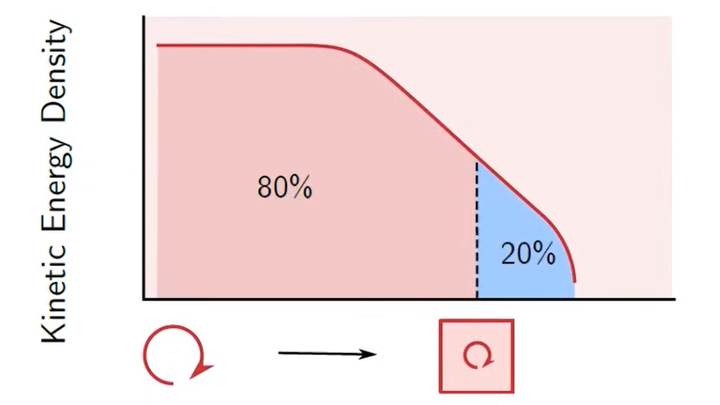image

但是怎么选择尺寸来使得达到这个80%湍动能解析的条件呢？为了解释这个事，首先要了解一下积分长度尺寸(Integral Length Scale)。

积分长度尺度

对于一个计算域而言，涡的尺度和能量在整个计算域内都有所不同：

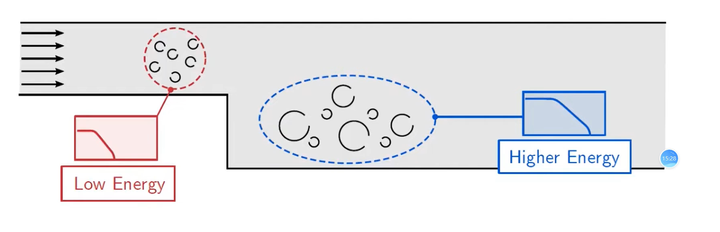image

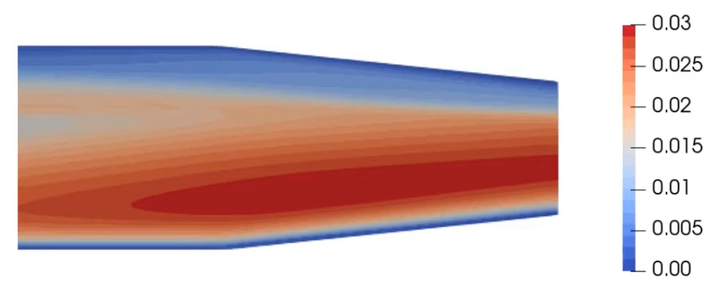
比如对于上面这一个后台阶流动来说，入口处的流动较为均匀，其湍动能低，而台阶后的回流严重，具有比较高的湍动能。

这时候我们需要用积分长度尺度来代表一个位置的所有涡，因为看一个值总比看每个位置的湍流能谱要简单：

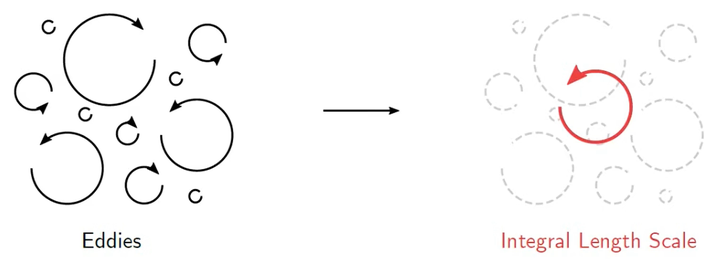image

积分长度尺度 $l_0$ 的定义就是在所有涡的平均湍动能用一个涡的长度来表示，即：

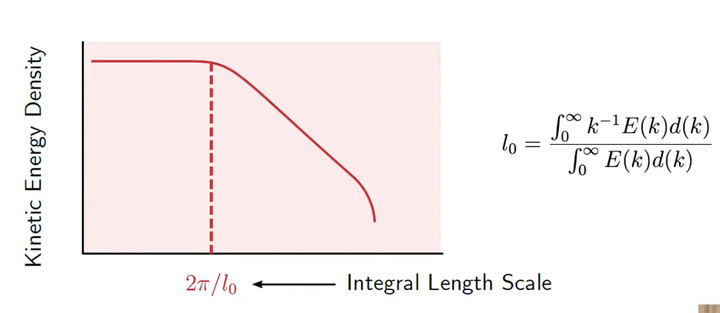$l_0=\frac{\int_{0}^\infty k^{-1} E(k)d(k)}{\int_{0}^\infty E(k)d(k)}$

image

根据定义，湍动能大的地方 $l_0$ 大，湍动能小的地方 $l_0$ 小。那么我们怎么获得这个 $l_0$ 呢？首先我们可以通过RANS方法把 $l_0$ 计算出来，比如说：

$k-\varepsilon$ 模型———— $l_0=\frac{k^{3/2}}{\varepsilon}$
$k-\omega$ 模型———— $l_0=\frac{k^{1/2}}{C_\mu\omega}$

最后通过计算，我们可以得到各个网格上的 $l_0$ ，比如说下图的样子：

image

当我们获得了 $l_0$ ,我们就可以计算网格的尺度了，比如说 $l_0$ 小的地方网格密， $l_0$ 大的地方网格稀。

image

一般来说，好的估算结果是最小网格尺度 $\Delta$ 是 $l_0$ 的五分之一，即：

$\Delta=\frac{l_0}{5}$

image

这时候我们就可以根据这个定义来定义一个新的量：

$f=\frac{l_0}{\Delta}=\frac{k^{3/2}}{\varepsilon\times \Delta}$

其中 $\Delta=\text{网格单元体积}^{1/3}$ 。

在后处理软件中把 $f$ 画出来，如果 $f$ 小于5，那么就说明网格太稀疏了，需要进一步加密。

总结

最小的网格尺寸决定了湍动能能被解析的范围。
越小的网格能够解析越大的能量。
好的LES要至少能解析80%的湍动能。
用五个网格来表示积分长度尺度是一个比较好的评估手段来保证80%的湍动能都能被解析。

第二部分

上一部分我们介绍了一些有关于LES的介绍性概念，比如说湍动能叶珊、积分长度尺寸以及如何为一个LES算例估算初始网格。

在第二部分，在我们算完了第一个LES算例之后，我们应该做什么？哪一类的量是我们需要关注的？它们代表着什么？你要怎么判断你所产生的初始网格对于一个实际的LES算例来说足够的好。

当我们计算一个LES之后，我们需要根据理论确定计算域中那一部分已经被充分解析，哪一部分则还需要继续细化。

这时候我们依然使用湍动能来评估网格是否充分，比如说好的LES算例能够解析至少80%的总的湍动能。当我们计算完之后，我们就需要判断我们解析了多少，是否有最少80%了？

为了计算上述的湍动能解析率，我们需要计算一些额外的量。

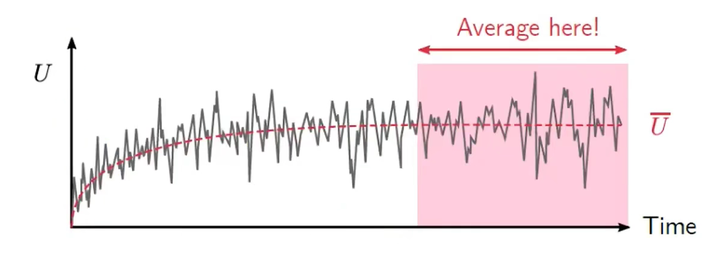
1.计算平均速度

在LES中，CFD代码计算了瞬时速度 $\mathbf{U}$ ，但是我们还要其时间平均的速度，即 $\bar{\mathbf{U}}$ 。

需要注意的是，我们计算的时候，需要要确定速度处于一个定常的状态，然后再进行平均，比如说如下：

image

2.计算脉动速度

瞬时速度减去平均速度，也就得到了脉动速度：

$u^\prime=U-\bar{U}$

我们使用脉动速度来计算湍动能.

3.解析的湍动能 $k_{res}$

湍动能的定义是：每单位重量的湍动能= $\frac{1}{2}u^2$ ，所以我们需要先将脉动速度乘在一起，即：

$u^\prime u^\prime~~u^\prime v^\prime~~u^\prime w^\prime~~v^\prime v^\prime~~v^\prime w^\prime~~w^\prime w^\prime$

再相乘之后，我们再给求一个时间平均，即：

$\overline{u^\prime u^\prime}~~\overline{u^\prime v^\prime}~~\overline{u^\prime w^\prime}~~\overline{v^\prime v^\prime}~~\overline{v^\prime w^\prime}~~\overline{w^\prime w^\prime}$

这些量最后都能被表示为解析的雷诺应力张量：

$\frac{R_{i j}}{\rho}=\left[\begin{array}{lll} \overline{u^{\prime} u^{\prime}} & \overline{u^{\prime} v^{\prime}} & \overline{u^{\prime} w^{\prime}} \\ \overline{v^{\prime} u^{\prime}} & \overline{v^{\prime} v^{\prime}} & \overline{v^{\prime} w^{\prime}} \\ \overline{w^{\prime} u^{\prime}} & \overline{w^{\prime} v^{\prime}} & \overline{w^{\prime} w^{\prime}} \end{array}\right]$

由于不同脉动速度乘积的顺序并不重要，所以对于上面的矩阵我们可以只用六个分量就能表示它，即：

$\frac{R_{i j}}{\rho}=\left[\begin{array}{lll} \overline{u^{\prime} u^{\prime}} & \overline{u^{\prime} v^{\prime}} & \overline{u^{\prime} w^{\prime}} \\ & \overline{v^{\prime} v^{\prime}} & \overline{v^{\prime} w^{\prime}} \\ & & \overline{w^{\prime} w^{\prime}} \end{array}\right]$

使用雷诺应力张量的对角元来计算解析的湍动能：

$k_{res}=\frac{1}{2}(\overline{u^\prime u^\prime}+\overline{v^\prime v^\prime}+\overline{w^\prime w^\prime})$

在OpenFOAM里面，用一个叫uPrime2Mean的矩阵表示了雷诺应力张量：

$\left[\begin{array}{lll} \overline{u^{\prime} u^{\prime}} & \overline{u^{\prime} v^{\prime}} & \overline{u^{\prime} w^{\prime}} \\ & \overline{v^{\prime} v^{\prime}} & \overline{v^{\prime} w^{\prime}} \\ & & \overline{w^{\prime} w^{\prime}} \end{array}\right]$

而在ANSYS里面，则是计算了 $\sqrt{\overline{(u^\prime)^2}}$ ,即

$U_{RMSE}=\sqrt{\overline{(u^\prime)^2}}$

也正是因此，计算湍动能时需要的是：

$k=\frac{1}{2}(U_{RMSE}^2+V_{RMSE}^2+W_{RMSE}^2)$

也就是说，当我们求解出一个LES结果时，我们需要通过后处理计算一个新的场 $k_{res}$ :

在openFOAM里面： $\text{kres=0.5*(UPrime2MeanXX+UPrime2MeanYY+UPrime2MeanZZ)}$
在ANSYS Fluent里面： $\text{kres=0.5*(URMSE*URMSE+VRMSE*VRMSE+WRMSE*WRMSE)}$

总的湍动能

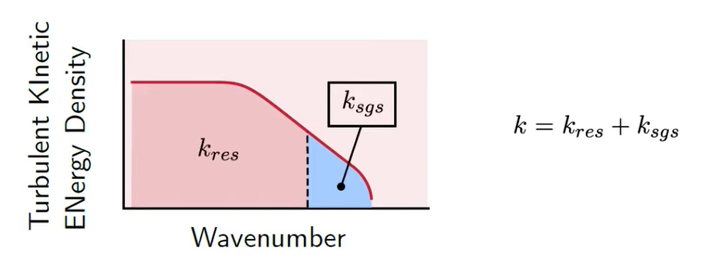
上面我们计算的是能被网格解析出的湍动能部分，但它并不是全部的湍动能，我们需要把亚格子湍动能也加上去：

image

所以实际上，我们是需要计算亚格子湍动能 $ksgs$ ：

在OpenFOAM里面，会默认计算 $k_{sgs}$ ，并且将其作为一个场写下来 $k$ 。
在ANSYS中，则需要在后处理软件中计算 $k_{sgs}$ 。

$k_{sgs}$ 的值取决于亚格子(SGS)模型。

如果使用的是湍动能输运模型，那么CFD代码求解 $k_{sgs}$ 为：

$\frac{\partial\left(\rho k_{s g s}\right)}{\partial t}+\nabla \cdot\left(\rho \boldsymbol{U} k_{s g s}\right)=\nabla \cdot\left(\rho D_{k} \nabla k_{s g s}\right)-C_{\epsilon} \frac{\rho k_{s g s}^{3 / 2}}{\Delta}+\rho G_{s g s}-\frac{2}{3} \rho k_{s g s} \nabla \cdot \boldsymbol{U}$

计算结果会直接输出，不需要在后处理中继续计算。

对于其他的SGS模型，则需要在后处理中计算 $k_{sgs}$ ，比如说我们可以从亚格子长度尺度 $l_{sgs}$ 来计算 $k_{sgs}$ ：

$k_{sgs}=(\frac{\mu_{sgs}}{\rho l_{sgs}})^2$

那么什么是 $l_{sgs}$ 呢？和积分长度尺度 $l_0$ 的定义一样， $l_{sgs}$ 代表了一个平均的涡的大小，也就是一个网格内，所有尺寸小于这个网格的涡的平均值。

$l_{sgs}$ 从定义上说就必须要小于网格的尺度，即：

$l_{sgs}=C_s*(\text{Cell Volume})^{1/3}$

$C_s=0.1$ 是Smagrinsky系数（关于这个模型的部分之后再说）。
$C_s<1$ ,因此这一长度总是小于网格尺度。

不过需要注意的是，靠近壁面的时候，涡会逐渐消散，对于一个具有比较大长细比的网格单元， $l_{sgs}$ 被与壁面的距离 $y$ 所限制，因此修正之后的计算 $l_{sgs}$ 法则为：

$l_{sgs}=min(\kappa y,C_s\Delta^{1/3})~~~\kappa=0.41$

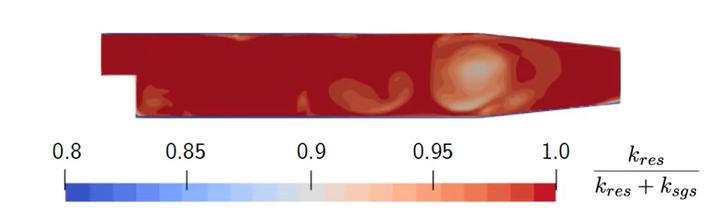
综上，我们有同时有了解析的湍动能 $k_{res}$ 和亚格子湍动能 $k_{sgs}$ ，进一步，我们可以在后处理中计算 $k_{res}/(k_{res}+k_{sgs})$ 。这时候，如果是一个好的算例，那么就需要在整个计算域内，这一比值都大于0.8。

image

那么根据获得的结果，我们就可以对网格进行进一步的细化。

总结

一个好的LES算例的网格需要至少能够解析80%的湍动能。
我们可以通过在后处理中计算 $k_{res}$ 和 $k_{sgs}$ 计算解析的湍动能占比。
$k_{sgs}$ 一般来说更难计算，它取决于你所采用的SGS模型。

第三部分

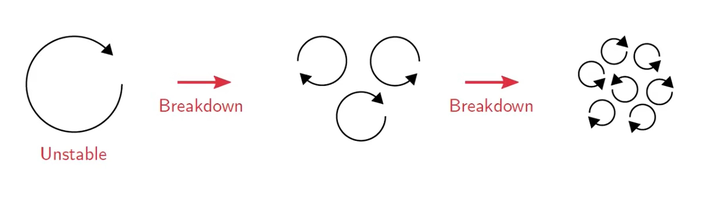
在实际的湍流中，湍流涡并不稳定，它会不断从大涡破碎成小涡，小涡破碎成更小的涡，直至小到某一个程度，被分子粘性耗散掉。

image

但是在隐式的LES中，我们只算计算出每个网格单元的速度，而一个速度没办法表示涡，因此我们没有办法在解析小于一个网格大小的涡。因此在上述所描述的过程成，当大涡不断的破碎，直到小到网格的尺寸后，我们就不能解析这个尺寸以下的涡了，因此这部分的涡无法继续破碎成小涡，而且由于其依然不够小，这个尺寸的涡也不会被分子粘性好散掉。

如果不对模型进行任何处理，最后导致的结果就是这部分无法被解析的涡会持续存在的，也不会进一步破碎，流动缺少了由湍动能转化为热能的过程，整个流动的湍动能会过高。

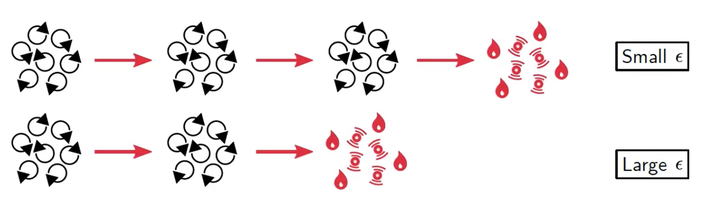
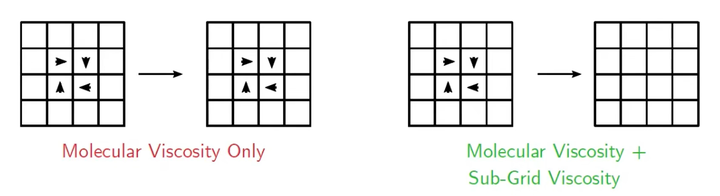
因此，为了模拟物理上涡破碎并耗散的过程，我们需要做的是通过添加湍流耗散率的方式，将刚好略微大于网格尺寸的涡(网格依然能够解析的涡)给耗散掉。

接下来，我们就讨论一下湍流耗散率。

湍流耗散率

湍流耗散率 $\varepsilon$ 指的是湍流转化为热能的速率，他的单位是每单位湍动能/每秒，即：

$\varepsilon\rightarrow\frac{[m^2]}{s^2}\frac{1}{s}=\frac{[m^2]}{s^3}$

通过增加湍流耗散率，我们能够增加湍流涡的耗散速度，即：

image

接下来介绍如何计算 $\varepsilon$ :

在实际湍流/DNS中，

$\varepsilon=\nu\frac{\partial U_i}{\partial x_j}\frac{\partial U_i}{\partial x_j}$

在RANS里面，我们通过是求解一个关于 $\varepsilon$ 的输运方程，但在LES里面并不是这样。

一般来说， $\varepsilon=\nu\frac{\partial U_i}{\partial x_j}\frac{\partial U_i}{\partial x_j}$ 中的分子粘性 $\nu$ 很小，随着涡逐渐变小，速度梯度逐渐增大，直到某个量级分子粘性足够将他们耗散掉，这需要非常非常密的网格，LES的网格一般是达不到那么密，因此我们需要考虑添加一个人工涡粘性来把恰好大于网格尺寸的涡耗散掉，即：

$\varepsilon=(\nu+\nu_{sgs})\frac{\partial U_i}{\partial x_j}\frac{\partial U_i}{\partial x_j}$

如果我们仔细指定 $\nu_{sgs}$ 的值，那么我们就能够达到恰好耗散掉略大于网格尺寸的涡的目的。

实际上，这个人工耗散就是为了模仿涡破碎的过程。

image

现在的问题就在于我们在LES中要怎么求解 $\varepsilon$ 。

现在我们看NS方程和连续方程：

$\frac{\partial \rho}{\partial t}+\frac{(\partial \rho U_j)}{\partial x_j}=0\\ \frac{\partial(\rho U_i)}{\partial t}+\frac{\partial}{\partial x_j}(\rho U_i U_j)=-\frac{\partial P}{\partial x_i}+\underbrace{\frac{\partial}{\partial x_j}(\tau_{ij})}_{粘性应力}$

其中， $\tau_{ij}$ 是粘性应力张量，它通过分子粘性将能量耗散掉。只有当涡足够小(小到Kolmogorov尺度时),分子粘性才算得上足够大，才能够将涡耗散掉。

在LES中，我们通过增加一个额外的应力项 $\tau_{sgs}$ 来增大耗散，且能够达到恰好耗散掉略大于网格的涡的要求。

$\frac{\partial \rho}{\partial t}+\frac{\partial (\rho U_j)}{\partial x_j}=0\\ \frac{\partial (\rho U_i)}{\partial t}+\frac{\partial }{\partial x_j}(\rho U_i U_j)=-\frac{\partial P}{\partial x_i}+\underbrace{\frac{\partial }{\partial x_j}(\tau_{ij}+\tau_{sgs})}_{粘性+亚格子}$

这一额外项可以通过“过滤”NS方程的方式由数学上推导出。

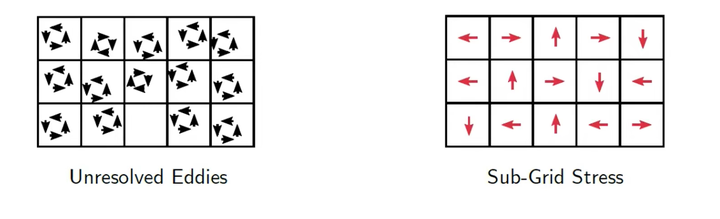
我们将小于网格尺寸的涡当作是一种阻力，即：

image

这一阻力能够耗散能量，并且将略大于网格尺寸的涡破碎掉。

通过涡粘性模型，我们可以计算出亚格子应力，即：

$\tau_{sgs}=2\rho \nu_{sgs}S_{ij}^{\star}-\frac{2}{3}\rho k_{sgs}\delta_{ij}$

其中， $S^{\star}_{ij}=\frac{1}{2}(\frac{\partial \overline{U}_i}{\partial x_j}+\frac{\partial \overline{U}_j}{\partial x_j}-\frac{1}{3}\frac{\partial \overline{U}_k}{\partial x_k}\delta_{ij})$

$S^{\star}_{ij}$ 时在CFD网格上解析的涡的应变率。
需要记住的是，虽然涡逐渐变小，速度梯度也就逐渐变大。
因此，最后应力会达到最大，并把涡耗散掉（涡的尺寸恰好大于网格尺寸）。

$\nu_{sgs}$ 控制了应力 $\tau_{sgs}$ 的强度，那么要如何计算 $\nu_{sgs}$ 呢？

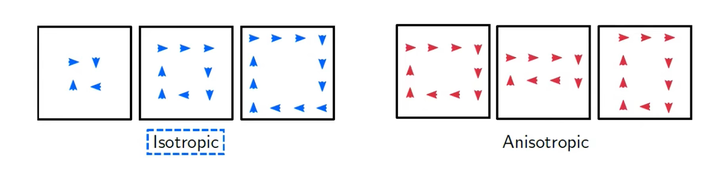
首先假设小于网格尺寸的涡时各向同性的，也就是说他们的形状相同，只是大小不同。

image

现在我们唯一需要考虑的就是涡的大小，不必考虑涡的尺寸。考虑到亚格子粘性是为了耗散掉略大于网格尺寸的涡，因此更大的网格就需要更大的亚格子粘性，所以实际上它是一个网格尺寸的函数： $\nu_{sgs}=f(\Delta)$ 。

因此，我们在每一个网格上，都需要求解一个不同的关于 $\nu_{sgs}$ 方程，正是这个原因，在LES中我们无法进行网格无关性验证，这时候唯一的标准往往就是是否解析了80%的湍动能。

总结

在LES中，略大于网格尺寸的涡往往不会破碎。
这些涡会在网格内长久的存在，不会耗散掉，并且导致湍动能过高。
为了模拟这部分涡的破碎过程，我们增加了耗散率 $\varepsilon$ 。
我们通过控制亚格子粘性 $\nu_{sgs}$ 来控制耗散率，这个 $\nu_{sgs}$ 是关于网格尺寸的函数。大的网格单元就需要更大的粘性。

本文使用 Zhihu On VSCode 创作并发布

posted @ 2022-03-11 15:57 Lagomgom 阅读(5250) 评论(2) 收藏举报

刷新页面返回顶部

Lagomgom

LES大涡模拟-【转载】第一部分 Eddies(涡)的解析

第一部分 Eddies(涡)的解析

波数k

积分长度尺度

总结

第二部分

1.计算平均速度

2.计算脉动速度

3.解析的湍动能

总的湍动能

总结

第三部分

湍流耗散率

总结

公告

3.解析的湍动能 $k_{res}$