HEOI2018(九省联考) 题解集合
转载请注明出处:http://www.cnblogs.com/LadyLex/p/8792894.html
今年的省选题目真是赞啊……Day2的题完全不会做……
不过终于卡着校线爬着进了B队
终于改完了题……在这里总结一下这次的题目吧
DAY1
Pro.1 一双木棋
这道题的确是T1难度的题目……
我们考虑这其实是个对抗搜索
已经放好棋子的位置只能是左上角,并且从上到下是不降的
如果我维护了现在已经放了棋子的位置,我就可以知道下一步该谁放,以及哪里可以放了
具体做法……我用11进制压位来着,出题人的做法是用01维护轮廓线
hashmap快的飞起
code:

1 #include <cstdio> 2 #include <cstring> 3 using namespace std; 4 #define RG register 5 #define LL long long 6 #define mod 612497 7 #define inf 0x3f3f3f3f 8 struct hash_map 9 { 10 struct node{LL state;int next,val;}s[200000]; 11 int e,adj[mod]; 12 inline void ins(LL state,int val) 13 { 14 RG int pos=state%mod; 15 s[++e].state=state;s[e].val=val;s[e].next=adj[pos];adj[pos]=e; 16 } 17 inline int get(LL state) 18 { 19 RG int pos=state%mod,i; 20 for(i=adj[pos];i&&s[i].state!=state;i=s[i].next); 21 if(!i)return -inf; 22 return s[i].val; 23 } 24 }H; 25 inline int min(int a,int b){return a<b?a:b;} 26 inline int max(int a,int b){return a>b?a:b;} 27 int n,m,A[15][15],B[15][15]; 28 LL bin[20]; 29 inline int dfs(int l,int r,LL state,int already) 30 { 31 if(already==n*m)return 0; 32 int ret=H.get(state); 33 if(ret!=-inf)return ret; 34 if(already&1)ret=inf; 35 int last=0; 36 for(RG int i=l;i<=r;++i) 37 { 38 int v=(state/bin[i-1])%11; 39 if(i!=l&&v==last)continue; 40 if(already&1)ret=min(ret,-B[i][v+1]+dfs(l+(v==m-1),r,state+bin[i-1],already+1)); 41 else ret=max(ret,A[i][v+1]+dfs(l+(v==m-1),r,state+bin[i-1],already+1)); 42 last=v; 43 } 44 if(r<n) 45 if(already&1)ret=min(ret,-B[r+1][1]+dfs(l,r+1,state+bin[r],already+1)); 46 else ret=max(ret,A[r+1][1]+dfs(l,r+1,state+bin[r],already+1)); 47 H.ins(state,ret); 48 return ret; 49 } 50 int main() 51 { 52 RG int i,j; 53 scanf("%d%d",&n,&m); 54 for(bin[0]=i=1;i<=15;++i) 55 bin[i]=bin[i-1]*11ll; 56 for(i=1;i<=n;++i) 57 for(j=1;j<=m;++j) 58 scanf("%d",&A[i][j]); 59 for(i=1;i<=n;++i) 60 for(j=1;j<=m;++j) 61 scanf("%d",&B[i][j]); 62 if(m==1) 63 { 64 int ans=0; 65 for(i=1;i<=n;++i) 66 if(i&1)ans+=A[i][1]; 67 else ans-=B[i][1]; 68 printf("%d\n",ans); 69 return 0; 70 } 71 printf("%d\n",A[1][1]+dfs(1,1,1,1)); 72 }
Pro.2 IIIDX
感觉又看到了UR17的滑稽树上滑稽果
出题人给了我这个贪心那他肯定是错的啊
真是见鬼……考场上我用分类讨论打了k=2的部分
但是我们可以考虑像出题人说的那样“换个贪心的思路”
我们不能往第一个节点放最大的元素是因为它的子树里面要有比他更大的对吧
考虑先从大到小排序,按照从1到n的顺序给每个节点填数
那么我们考虑某个节点选的时候,选能选的最大值,然后给他的子树预留一定数量比他大的数
预留的意思是,我们并不知道谁会被用,但是这个范围里面已经有这么多不能用了
我们用线段树维护每个数”比他大的数还有几个可用的“,
每次我们在线段树上查询一个最小的位置x,使得其右面的数的可用个数都大于等于这个节点的子树大小
然后给$[x,n]$区间减去$size[x]-1$
这样为什么是对的?我们不能把任何一个点的可用数量减成负的
因此我们要这样做
而如何查询这个位置呢?我个人维护了线段右端点的值和线段最小值
因为可用位置的序列是一堆不降序列,那么查询的时候,左线段最小值最大的后缀一定是”只选最后一个位置“这个后缀
因此用上面这俩信息就能维护了。
code:

1 #include <cstdio> 2 #include <cstring> 3 #include <algorithm> 4 #include <cmath> 5 using namespace std; 6 #define RG register 7 #define db double 8 #define N 500010 9 #define inf 0x3f3f3f3f 10 char B[1<<15],*S=B,*T=B; 11 #define getc (S==T&&(T=(S=B)+fread(B,1,1<<15,stdin),S==T)?0:*S++) 12 inline int read() 13 { 14 RG int x=0;RG char c=getc; 15 while(c<'0'|c>'9')c=getc; 16 while(c>='0'&c<='9')x=10*x+(c^48),c=getc; 17 return x; 18 } 19 inline bool mt(const int &a,const int &b){return a>b;} 20 struct node 21 { 22 node *ch[2];int rval,minn,mark; 23 }*root,mem[N<<1];int tot; 24 inline node* build(int l,int r) 25 { 26 node *o=mem+(tot++); 27 o->rval=r;o->minn=l; 28 if(l^r) 29 { 30 RG int mi=l+r>>1; 31 o->ch[0]=build(l,mi); 32 o->ch[1]=build(mi+1,r); 33 } 34 return o; 35 } 36 #define min(a,b) ((a)<(b)?(a):(b)) 37 inline int find(node *&o,int l,int r,int K) 38 { 39 if(l==r)return l; 40 RG int mi=l+r>>1,ret; 41 if(o->mark) 42 o->ch[0]->minn+=o->mark,o->ch[0]->rval+=o->mark,o->ch[0]->mark+=o->mark, 43 o->ch[1]->minn+=o->mark,o->ch[1]->rval+=o->mark,o->ch[1]->mark+=o->mark, 44 o->mark=0; 45 if( min(o->ch[0]->rval,o->ch[1]->minn) >= K )ret=find(o->ch[0],l,mi,K); 46 else ret=find(o->ch[1],mi+1,r,K); 47 o->minn=min(o->ch[0]->minn,o->ch[1]->minn); 48 o->rval=o->ch[1]->rval; 49 return ret; 50 } 51 inline void add(node *&o,int l,int r,int L,int R,int val) 52 { 53 if(L<=l&&r<=R) 54 {o->minn+=val,o->rval+=val,o->mark+=val;return;} 55 RG int mi=l+r>>1; 56 if(o->mark) 57 o->ch[0]->minn+=o->mark,o->ch[0]->rval+=o->mark,o->ch[0]->mark+=o->mark, 58 o->ch[1]->minn+=o->mark,o->ch[1]->rval+=o->mark,o->ch[1]->mark+=o->mark, 59 o->mark=0; 60 if(L<=mi)add(o->ch[0],l,mi,L,R,val); 61 if(mi<R)add(o->ch[1],mi+1,r,L,R,val); 62 o->minn=min(o->ch[0]->minn,o->ch[1]->minn); 63 o->rval=o->ch[1]->rval; 64 } 65 int n,d[N],size[N],pos[N],fa[N],lst[N]; 66 db k;bool killed[N]; 67 int main() 68 { 69 RG int i,j,u,v; 70 scanf("%d%lf",&n,&k); 71 for(i=1;i<=n;++i)d[i]=read(); 72 for(i=n;i;--i) 73 ++size[i],fa[i]=floor(i/k),size[fa[i]]+=size[i]; 74 sort(d+1,d+n+1,mt); 75 for(lst[n]=n,i=n-1;i;--i) 76 lst[i]=(d[i]==d[i+1])?lst[i+1]:i; 77 root=build(1,n); 78 killed[0]=1; 79 for(i=1;i<=n;++i) 80 { 81 if(!killed[fa[i]]) 82 add(root,1,n,pos[fa[i]],n,size[fa[i]]-1),killed[fa[i]]=1; 83 pos[i]=lst[find(root,1,n,size[i])]; 84 add(root,1,n,pos[i],n,-size[i]); 85 printf("%d ",d[pos[i]]); 86 } 87 }
Pro.3 coat
看来出题人的数据的确造水了……
一开始想了一个$O(n^3)$的做法,就是我们把val>=x的点看成黑点,剩下的是白点
然后我们从大到小枚举x,每次统计黑点大于等于x的联通块数,每次新增的联通块就是新的这个值为K大值的联通块数
我们这样就可以统计答案了对吧
然后我想了几个剪枝
*我们当然要离散,也就是并不统计所有的1~W
*一个显然的剪枝是如果总黑点数小于K,就直接continue
*枚举的时候,每个点的size定义为子树内的黑点数
*我们可以把枚举范围限制为K(大于K的变量我们都加到到K处),这样如果K很小的话我们可以跑的快一点
然后这样复杂度最后就被优化成了$O(nk(n-k))$
事实证明由于出题人的数据水了(n,k接近),所以这个做法在考场上拿了95分
其他省份的同学有用这个做法A题的,事实证明是我实现的细节不优秀,导致常数太大了
正解的做法我实在不敢尝试……不是很懂……
code:

1 #include <cstdio> 2 #include <cstring> 3 #include <algorithm> 4 using namespace std; 5 #define RG register 6 #define LL long long 7 #define mod 64123 8 #define N 1700 9 int n,K,e,adj[N],size[N],sta[N],val[N],top; 10 struct edge{int zhong,next;}s[N<<1]; 11 inline void add(int qi,int zhong) 12 {s[++e].zhong=zhong;s[e].next=adj[qi];adj[qi]=e;} 13 // inline int min(int a,int b){return a<b?a:b;} 14 #define min(a,b) ((a)<(b)?(a):(b)) 15 int f[N][N],cnt,can[N]; 16 LL g[N]; 17 inline void dfs(int rt,int fa) 18 { 19 RG int i,to,u,v,j,k,lim1,lim2,lim3,lim4; 20 memset(f[rt],0,K+5<<2); 21 f[rt][can[rt]]=1; 22 for(i=adj[rt];i;i=s[i].next) 23 if((to=s[i].zhong)!=fa) 24 { 25 dfs(to,rt); 26 memset(g,0,K+5<<3); 27 lim1=min(can[rt],K); 28 lim2=min(can[to],K); 29 for(j=0;j<=lim1;++j) 30 for(v=0;v<=lim2;++v) 31 g[min(K,j+v)]=g[min(K,j+v)] + (LL)f[rt][j]*f[to][v]; 32 can[rt]+=can[to]; 33 lim1=min(can[rt],K); 34 for(k=0;k<=lim1;++k)f[rt][k]=g[k]%mod; 35 } 36 ++f[rt][0]; 37 if(can[rt]>=K)cnt=(cnt+f[rt][K])%mod; 38 } 39 int main() 40 { 41 RG int i,j,a,b; 42 scanf("%d%d%d",&n,&K,&top); 43 for(i=1;i<=n;++i)scanf("%d",&val[i]),sta[i]=val[i]; 44 sort(sta+1,sta+n+1); 45 top=unique(sta+1,sta+n+1)-sta-1; 46 for(i=1;i<=n;++i) 47 val[i]=lower_bound(sta+1,sta+top+1,val[i])-sta; 48 for(i=1;i<n;++i) 49 scanf("%d%d",&a,&b),add(a,b),add(b,a); 50 RG int ans=0,last=0,tot; 51 for(i=top;i;--i) 52 { 53 tot=0; 54 for(j=1;j<=n;++j) 55 can[j]=(val[j]>=i),tot+=can[j]; 56 if(tot<K)continue; 57 cnt=0;dfs(1,0); 58 ans=(ans+(LL)(cnt-last)*sta[i])%mod; 59 last=cnt; 60 } 61 printf("%d\n",(ans+mod)%mod); 62 }
DAY2
Pro.1 劈配
考试的时候想对了也想错了
我把除了”如何匹配“其他的所有地方都想到了,就是匹配不对……
我们考虑枚举每个人的答案是第几志愿,然后向对应志愿的导师连边
导师就暴力拆成b个点即可
用二分图的增广来判断是否可行
然后第二问就通过二分转成第一问的判断
听起来很清真,但是为什么可以暴力拆成b个点?

code:

1 #include <cstdio> 2 #include <cstring> 3 #include <vector> 4 using namespace std; 5 #define RG register 6 #define N 210 7 int n,m,C,rk[N][N],lim[N],ned[N],T,vis[N*N],ans[N]; 8 struct edge{int zhong,next;}s[N*N<<5]; 9 struct Gragh 10 { 11 int e,adj[N],match[N*N]; 12 inline void init() 13 { 14 memset(match,0,sizeof(match)); 15 memset(adj,0,sizeof(adj));e=0; 16 } 17 inline void add(int qi,int zhong) 18 {s[++e].zhong=zhong;s[e].next=adj[qi];adj[qi]=e;} 19 inline bool find(int rt) 20 { 21 for(RG int u,i=adj[rt];i;i=s[i].next) 22 if(vis[u=s[i].zhong]!=T) 23 { 24 vis[u]=T; 25 if(!match[u]||find(match[u])) 26 {match[u]=rt;return 1;} 27 } 28 return 0; 29 } 30 }G,H; 31 vector<int>tea[N][N]; 32 inline bool check(int rt,int up) 33 { 34 H.init(); 35 for(RG int i=1;i<=up;++i) 36 if(ans[i]<=m) 37 for(vector<int>::iterator it =tea[i][ans[i]].begin();it!=tea[i][ans[i]].end();++it) 38 for(RG int k=1;k<=lim[*it];++k)H.add(i,(*it-1)*n+k); 39 for(RG int i=1;i<=up;++i)++T,H.find(i); 40 RG int cur=H.e; 41 for(RG int j=1;j<=ned[rt];++j) 42 if(!tea[rt][j].empty()) 43 { 44 H.e=cur;H.adj[rt]=0;++T; 45 for(vector<int>::iterator it =tea[rt][j].begin();it!=tea[rt][j].end();++it) 46 for(RG int k=1;k<=lim[*it];++k)H.add(rt,(*it-1)*n+k); 47 if(H.find(rt))return true; 48 } 49 return false; 50 } 51 int main() 52 { 53 RG int i,j,t,l,r,mi,fin; 54 scanf("%d%d",&t,&C); 55 while(t--) 56 { 57 scanf("%d%d",&n,&m); 58 memset(vis,0,sizeof(vis));T=0; 59 for(i=1;i<=m;++i)scanf("%d",&lim[i]); 60 for(i=1;i<=n;++i) 61 for(j=1;j<=m;++j)tea[i][j].clear(); 62 for(i=1;i<=n;++i) 63 for(j=1;j<=m;++j) 64 scanf("%d",&rk[i][j]), 65 tea[i][rk[i][j]].push_back(j); 66 for(i=1;i<=n;++i)scanf("%d",&ned[i]); 67 RG int cur; 68 for(G.init(),i=1;i<=n;++i) 69 { 70 cur=G.e; 71 for(ans[i]=m+1,j=1;j<=m;++j) 72 if(!tea[i][j].empty()) 73 { 74 G.e=cur; 75 G.adj[i]=0;++T; 76 for(vector<int>::iterator it =tea[i][j].begin();it!=tea[i][j].end();++it) 77 for(RG int k=1;k<=lim[*it];++k)G.add(i,(*it-1)*n+k); 78 if(G.find(i)){ans[i]=j;break;} 79 } 80 } 81 for(i=1;i<=n;++i)printf("%d ",ans[i]);printf("\n"); 82 for(i=1;i<=n;++i) 83 { 84 if(ans[i]<=ned[i]){printf("0 ");continue;} 85 l=0,r=i-1,fin=-1; 86 while(l<=r) 87 if(check(i,mi=l+r>>1))fin=mi,l=mi+1; 88 else r=mi-1; 89 printf("%d ",i-1-fin); 90 }printf("\n"); 91 } 92 }
Pro.2 林克卡特树
这题的正解似乎是之前遇到过的wqs二分
我们根本不可以发现”删掉K条边“等价于”选取K+1条不相交的链,使其权值和最大“
那么我们就可以写一个dp,数组定义是$f(i,j,0/1/2)$代表i的子树,选了j条链,i的度数为0/1/2
然后用儿子来更新父亲
这个dp细节特别多,可以获得60分
然后我们也不知道怎么就意识到,如果设$ans(x)$为选$x$条链的答案,那么这个$ans()$函数是上凸的
这其实可以理解,随着我们能删的边数变多,我们去掉了更多负权边影响,
但是删的更多后,我们就不得不删掉一些正权边,答案就变小了
这样我们可以用一条直线去卡这个凸包
假如在知道斜率后我们可以计算出这条直线的切点,那么我们通过二分斜率使得这个直线能在横坐标K处与凸包相切我们输出y坐标就行了
怎么算切点?斜率的实际意义相当于每选一条链要额外给答案减去斜率k那么多
这样计算我们得到一个答案$y_{0}$,那么$y_{0}+x*k$就是原来的$ans(x)$
因此我们通过一个$O(n)$的树归求出斜率为k时的切点,然后二分就行了
那个树归其实和贪心比较类似……?
整数二分需要注意一下如何判断边界
code:

1 #include <cstdio> 2 #include <cstring> 3 #include <algorithm> 4 using namespace std; 5 #define N 300010 6 #define RG register 7 #define LL long long 8 #define inf 0x3f3f3f3f3f3f3f3fll 9 int n,K,e,adj[N]; 10 struct edge{int zhong,val,next;}s[N<<1]; 11 inline void add(int qi,int zhong,int val) 12 {s[++e].zhong=zhong;s[e].next=adj[qi];adj[qi]=e;s[e].val=val;} 13 LL sum1[N],sum2[N]; 14 int num1[N],num2[N],sta[N],top,fa[N]; 15 inline void dfs1(int rt,int Vater) 16 { 17 sta[++top]=rt;fa[rt]=Vater; 18 for(RG int u,i=adj[rt],v;i;i=s[i].next) 19 if((u=s[i].zhong)!=Vater)dfs1(u,rt); 20 } 21 inline void check(int val) 22 { 23 RG int i,j,rt,u,v; 24 LL maxsum,secsum,tmpsum; 25 int maxnum,secnum,tmpnum; 26 for(j=n;j;--j) 27 { 28 rt=sta[j]; 29 num1[rt]=sum1[rt]=0;num2[rt]=sum2[rt]=0; 30 maxsum=secsum=0;maxnum=secnum=0; 31 for(i=adj[rt];i;i=s[i].next) 32 if((u=s[i].zhong)!=fa[rt]) 33 { 34 num1[rt]+=num1[u],sum1[rt]+=sum1[u]; 35 tmpsum=sum2[u]-sum1[u]+s[i].val,tmpnum=num2[u]-num1[u]; 36 if(tmpsum>maxsum||(tmpsum==maxsum&&tmpnum<maxnum)) 37 secsum=maxsum,secnum=maxnum,maxnum=tmpnum,maxsum=tmpsum; 38 else if(tmpsum>secsum||(tmpsum==secsum&&tmpnum<secnum)) 39 secnum=tmpnum,secsum=tmpsum; 40 } 41 num2[rt]=num1[rt]+maxnum;sum2[rt]=sum1[rt]+maxsum; 42 if(maxsum+secsum>val) 43 num1[rt]+=maxnum+secnum+1,sum1[rt]+=maxsum+secsum-val; 44 } 45 } 46 int main() 47 { 48 RG int i,x,a,b,c; 49 scanf("%d%d",&n,&K);++K; 50 for(i=1;i<n;++i) 51 scanf("%d%d%d",&a,&b,&c),add(a,b,c),add(b,a,c); 52 dfs1(1,0); 53 int l=-1e9,r=1e9,mi,ans; 54 while(l<=r) 55 { 56 mi=l+r>>1;check(mi); 57 if(num1[1]>K)l=mi+1; 58 else ans=mi,r=mi-1; 59 } 60 check(ans); 61 printf("%lld\n",sum1[1]+(LL)K*ans); 62 }
Pro.3 制胡窜
垃圾YJQ,毁我青春
这B题考场给我std我都抄不完2333333
我讲个笑话,我在考场上想到了正难则反,并且打出了后缀自动机+倍增+可持久化数据结构
最后打了个$N^{2}Q$暴力
我都佩服我自己
大概经过就是我用上面那堆东西维护了一个right集合
然后就死了,还不如人家kmp选手
那么怎么做呢?
我们考虑正难则反,那就是要维护一些方案数,使得每个字符串内部都有一个端点
让我偷张图
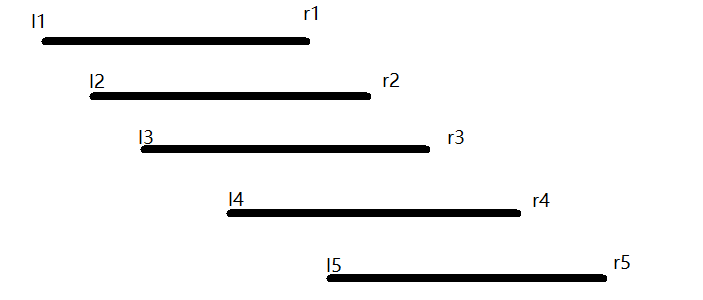
那么,比如我左端点在$(l1,l2)$,那么右端点应该覆盖后面4个串,即应该在$(l5,r2)$
那么写成通式应该是$\sum (r_{i+1}-r_{i})*(r_{i+1}-l_{n})$
我们分别维护$\sum (r_{i+1}-r_{i})*r_{i+1}$以及$\sum (r_{i+1}-r_{i})$
然后就能计算答案了
当然最恶心的地方是边界讨论
第一,可能不存在不合法的情况,这个可以判掉
第二,有的情况可以一个端点完全覆盖所有串,另外一个就可以随便移动了,这个也要统计上
最后,我们最后一个能覆盖的端点的计算不是$(r_{i+1}-r_{i})*(r_{i+1}-l_{n})$,而是$(r_{1}-l_{i})*(r_{i+1}-l_{n})$
code:

1 #include <cstdio> 2 #include <cstring> 3 #include <algorithm> 4 #include <cstdlib> 5 #include <iostream> 6 #include <vector> 7 using namespace std; 8 #define N 100010 9 #define inf 0x3f3f3f3f 10 #define fir first 11 #define sec second 12 #define RG register 13 #define LL long long 14 struct node 15 { 16 int sum1,minn,maxn,size; 17 LL sum2; 18 node *ch[2]; 19 inline void upd(); 20 }*root[N<<1],Mem[N<<7],*null;int tot; 21 char str[N]; 22 int n,q,len,ch[N<<1][10],parent[N<<1],maxn[N<<1],sz,last; 23 inline int newSAM(int l) 24 {maxn[++sz]=l;root[sz]=null;return sz;} 25 inline void init() 26 { 27 null=new node(); 28 null->ch[0]=null->ch[1]=null; 29 null->sum1=null->sum2=0; 30 null->minn=inf,null->maxn=-inf; 31 last=newSAM(0); 32 } 33 int f[N<<1][19],bin[30]; 34 inline void insert(int d) 35 { 36 RG int p=last,np=newSAM(maxn[p]+1),q,nq; 37 for(;p&&!ch[p][d];p=parent[p])ch[p][d]=np; 38 if(!p)parent[np]=1; 39 else 40 { 41 q=ch[p][d]; 42 if(maxn[q]==maxn[p]+1)parent[np]=q; 43 else 44 { 45 nq=newSAM(maxn[p]+1);memcpy(ch[nq],ch[q],sizeof(ch[q])); 46 parent[nq]=parent[q],parent[q]=parent[np]=nq; 47 for(;p&&ch[p][d]==q;p=parent[p])ch[p][d]=nq; 48 } 49 }last=np; 50 } 51 int deep[N<<1],pos[N],e,adj[N<<1]; 52 struct edge{int zhong,next;}s[N<<1]; 53 inline void add(int qi,int zhong) 54 {s[++e].zhong=zhong;s[e].next=adj[qi];adj[qi]=e;} 55 inline void dfs(int rt) 56 { 57 58 RG int i,u; 59 for(i=1;bin[i]<=deep[rt];++i) 60 f[rt][i]=f[f[rt][i-1]][i-1]; 61 for(i=adj[rt];i;i=s[i].next) 62 deep[u=s[i].zhong]=deep[rt]+1, 63 f[u][0]=rt,dfs(u); 64 } 65 inline int getid(int l,int r) 66 { 67 68 int rt=pos[r]; 69 for(RG int i=18;~i;--i) 70 if(maxn[f[rt][i]]>=len)rt=f[rt][i]; 71 return rt; 72 } 73 inline node* newnode() 74 { 75 node *o=Mem+(tot++); 76 o->ch[0]=o->ch[1]=null; 77 o->sum1=o->sum2=0;o->size=0; 78 return o; 79 } 80 inline void node::upd() 81 { 82 size=ch[0]->size+ch[1]->size; 83 minn=(ch[0]==null)?ch[1]->minn:ch[0]->minn; 84 maxn=(ch[1]==null)?ch[0]->maxn:ch[1]->maxn; 85 sum1=maxn-minn; 86 sum2=ch[0]->sum2+ch[1]->sum2; 87 if(ch[0]!=null&&ch[1]!=null) 88 sum2+=(LL)ch[1]->minn*(ch[1]->minn-ch[0]->maxn); 89 } 90 inline void ins(node *&o,int l,int r,int pos) 91 { 92 if(o==null)o=newnode(); 93 o->size=1;o->minn=o->maxn=pos; 94 if(l==r)return; 95 RG int mi=l+r>>1; 96 if(pos<=mi)ins(o->ch[0],l,mi,pos); 97 else ins(o->ch[1],mi+1,r,pos); 98 } 99 inline void merge(node *&a,node *b) 100 { 101 if(a==null){a=b;return;} 102 if(b==null)return; 103 merge(a->ch[0],b->ch[0]); 104 merge(a->ch[1],b->ch[1]); 105 a->upd(); 106 } 107 #define pll pair<LL,LL> 108 #define pii pair<int,int> 109 inline void query_pre(node *o,int l,int r,int pos,pii &q) 110 { 111 if(l==r){q.fir=l;++q.sec;return;} 112 RG int mi=l+r>>1; 113 if(o->ch[1]!=null&&o->ch[1]->minn<pos)q.sec+=o->ch[0]->size,query_pre(o->ch[1],mi+1,r,pos,q); 114 else query_pre(o->ch[0],l,mi,pos,q); 115 } 116 inline void query_nxt(node *o,int l,int r,int pos,pii &q) 117 { 118 if(l==r){q.fir=l;--q.sec;return;} 119 RG int mi=l+r>>1; 120 if(o->ch[0]!=null&&o->ch[0]->maxn>pos) 121 q.sec-=o->ch[1]->size,query_nxt(o->ch[0],l,mi,pos,q); 122 else query_nxt(o->ch[1],mi+1,r,pos,q); 123 } 124 inline int query_kth(node *o,int l,int r,int k) 125 { 126 if(l==r)return l; 127 return (o->ch[0]->size>=k)?query_kth(o->ch[0],l,(l+r>>1),k):query_kth(o->ch[1],(l+r>>1)+1,r,k-o->ch[0]->size); 128 } 129 inline void query(node *o,int l,int r,int L,int R,pll &q) 130 { 131 if(o==null)return; 132 if(L<=l&&r<=R) 133 {q.fir+=o->sum1,q.sec+=o->sum2;return;} 134 RG int mi=l+r>>1; 135 if(R<=mi)query(o->ch[0],l,mi,L,R,q); 136 else if(mi<L)query(o->ch[1],mi+1,r,L,R,q); 137 else 138 { 139 if(o->ch[0]!=null&&o->ch[1]!=null) 140 { 141 int v1=o->ch[1]->minn-o->ch[0]->maxn; 142 q.fir+=v1,q.sec+=(LL)v1*o->ch[1]->minn; 143 } 144 query(o->ch[0],l,mi,L,R,q); 145 query(o->ch[1],mi+1,r,L,R,q); 146 } 147 } 148 struct quest{int len;LL ans;}Q[N*3]; 149 vector<int>mem[N<<1]; 150 inline LL S(int l,int r){return (LL)(r-l+1)*(l+r)/2;} 151 inline void work(int rt) 152 { 153 RG int i; 154 for(i=adj[rt];i;i=s[i].next) 155 work(s[i].zhong),merge(root[rt],root[s[i].zhong]); 156 pii Ln,R1;pll ans; 157 RG int r1=root[rt]->minn,lx,ln; 158 for(vector<int>::iterator it=mem[rt].begin();it!=mem[rt].end();++it) 159 { 160 len=Q[*it].len; 161 ln=root[rt]->maxn-len+1; 162 if(root[rt]->size==1) 163 {Q[*it].ans-=(LL)(len-1)*(ln-1)+S(n-r1,n-(ln+1));continue;} 164 R1.sec=0,Ln.sec=root[rt]->size+1; 165 query_pre(root[rt],1,n,r1+len-1,R1);query_nxt(root[rt],1,n,ln,Ln); 166 lx=R1.fir-len+1; 167 if(R1.sec+1<Ln.sec)continue; 168 if(R1.sec+1==Ln.sec){Q[*it].ans-=(LL)(r1-lx)*(Ln.fir-ln);continue;} 169 if(Ln.sec==1) 170 { 171 Q[*it].ans-=(LL)(r1-len)*(r1-lx)+S(n-r1,n-lx-1); 172 Q[*it].ans-=root[rt]->sum2-(LL)root[rt]->sum1*ln; 173 } 174 else 175 { 176 Q[*it].ans-=(LL)(r1-lx)*( query_kth(root[rt],1,n,R1.sec+1)-ln ); 177 if(Ln.sec<=R1.sec) 178 { 179 ans.fir=ans.sec=0; 180 query(root[rt],1,n,query_kth(root[rt],1,n,Ln.sec-1),R1.fir,ans); 181 Q[*it].ans-=ans.sec-ans.fir*ln; 182 } 183 } 184 } 185 } 186 int main() 187 { 188 RG int i,j,l,r,id; 189 scanf("%d%d%s",&n,&q,str+1); 190 init(); 191 for(i=1;i<=n;++i) 192 insert(str[i]-'0'),pos[i]=last, 193 ins(root[last],1,n,i); 194 for(i=2;i<=sz;++i)add(parent[i],i); 195 for(bin[0]=i=1;i<=25;++i)bin[i]=bin[i-1]<<1; 196 deep[1]=1;dfs(1); 197 LL all=(n-1ll)*(n-2)/2; 198 for(i=1;i<=q;++i) 199 { 200 scanf("%d%d",&l,&r); 201 len=Q[i].len=r-l+1,Q[i].ans=all; 202 mem[getid(l,r)].push_back(i); 203 } 204 work(1); 205 for(i=1;i<=q;++i)printf("%lld\n",Q[i].ans); 206 }
总结
这次DAY1的难度还算适中吧……至少不会爆零……
然后DAY2的题目就非常有难度了,然后我就死了
感觉考试的时候,DAY1节奏很好,DAY2由于题目太难,没有适当的放松
然后就比较紧张,可能也影响了思维的活跃度和严密性
以后看到难题之后不要乱了阵脚,慢慢的做,拿好每一档能拿的分数
继续前行吧。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号