[您有新的未分配科技点]计算几何入门(1):点,向量以及向量的简单应用
在打了一阵数据结构之后,老师表示“今天晚上让学长给你们讲一下计算几何”……然后就死了.jpg
昨天晚上一直在推数学的式子以及回顾讲课的笔记……计算几何特点就是多而杂,即使是入门部分也是如此……
首先,我们从二维的几何问题开始处理。
我们知道,高中解析几何计算几何的基础是向量(Vector)和点(Point),所以我们先来表示这两个概念:
在计算几何中,点和向量一般用结构体来存储,像这样:
1 struct Point 2 { 3 double x,y,rad; 4 Point(double xx=0,double yy=0){x=xx,y=yy;} 5 }; 6 typedef Point Vector;
由于向量和点表示方式是相同的,但是我们并不能给点加减。
所以我们给Point起一个别名,这样用的时候就不会引起歧义了。
接下来,我们考虑实现一些基本操作:向量求长度,加减,旋转,点积和叉积,两向量所成角。
向量加减可以通过重载来实现,点积和叉积记住公式直接算就可以,旋转可以通过计算三角函数展开现推……
所以其实都是板子。代码见下:
1 Vector operator + (Vector a,Vector b){return Vector(a.x+b.x,a.y+b.y);}//加 2 Vector operator - (Vector a,Vector b){return Vector(a.x-b.x,a.y-b.y);}//减 3 inline double Dot(Vector a,Vector b){return a.x*b.x+a.y*b.y;}//点积 4 inline double length(Vector a){return sqrt(Dot(a,a));}//长度 5 inline Vector Rotate(Vector a,double rad) 6 {return Vector(a.x*cos(rad)-a.y*sin(rad),a.x*sin(rad)+a.y*cos(rad));}//旋转 7 inline double Cross(Vector a,Vector b){return a.x*b.y-a.y*b.x;}//叉积 8 inline double Angle(Vector a,Vector b){return acos(Dot(a,b)/length(a)/length(b));}//角度
在有了这些基本的操作,尤其是叉积之后,我们就可以解决更多的问题了。
所以我们先展开了解一下叉积。
叉积,表示的是一种“有向面积”,其计算定义为(x1,y1)×(x2,y2)=x1*y2-x2*y1 ①
之所以称它为有向面积,是因为事实上叉积的结果是一个向量c,其长度有|c|=|a|*|b|*sinΘ
从①式我们容易发现,a×b和b×a似乎是不同的。
事实上,的确如此,对于向量叉积有a×b=-(b×a)这也正说明了叉积“有向”的特点:
因为把a旋转到b经过的角度和把b旋转到a经过的角度恰好是相反的,因此其结果相反。
有了这个“有向面积“,我们就可以解决不少问题了。
首先,我们先来考虑一系列求多边形面积的题目:
例1:给三点坐标,求三角形面积。
设三个点与原点连线的向量为a,b,c,那么有(b-a)×(c-a)=2*S三角形。计算即可。
大概长这样:
inline double Area2(Point a,Point b,Point c){return Cross(b-a,c-a);}
例2:给顶点坐标,求多边形面积。
最朴素的做法是把n边形剖分成n-2个三角形,但我们有更高效的做法。
在这之前,我们先要了解极角的概念。
极角表示一个向量与x轴正半轴所成的角,范围为[-π,π]。在C++中,求向量(x,y)的极角可以使用函数atan2
写法为atan2(y,x),需要调用cmath库
了解了极角之后,我们就可以讨论求多边形面积的问题了:
按照极角从小到大(逆时针顺序)给向量v1=(x1,y1)……vn=(xn,yn)排序,然后计算(v1×v2+v2×v3……vn×v1)/2即可
由于叉积有正有负,所以在计算一圈之后我们就正好得到了多边形的面积,这实际上还是一个三角剖分。
有兴趣的同学可以自己推一下式子。不过,在代码实现时我们一般以最左下角的点作为向量的起点。
下面给出一份简单的代码(设点已经按逆时针排序,编号0~n-1):
double ans=0; for(int i=1;i<n-1;i++) ans+=Cross(p[i]-p[0],p[i+1]-p[0]); printf("%.2lf\n",ans/2);
接下来,我们考虑一种求相交性的问题。
例3:给出四点A,B,C,D坐标,求AB,CD两直线交点O坐标。
首先,我们来考虑一条线段的“分点".(下面开始盗图)

上面这个式子感性理解一下就可以明白:如果λ1无限大,C就无限接近B,而上式也正好无限接近λ1B/λ1=B。
然后,我们就可以利用分点去求直线的交点了。
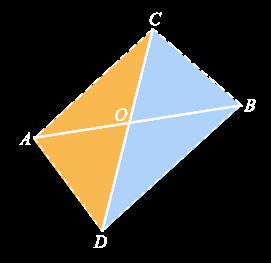
首先,我们要排除平行和重合的情况
我们思考一下,假设|AO|/|OB|=λ,那么就会有
|AO|/|OB|=S△ ADC/S△BDC=(AD×AC)/2 /(BC×BD)/2
这样,我们就可以用叉积算出分点的λ,然后用分点计算O点坐标即可。
特别注意,对于上图,上式中A与B叉积的顺序相反。
这一点不难看出其正确性,有兴趣的读者可以思考下为什么(提示:分类讨论,考虑分点的计算公式)
代码见下:
1 Vector operator * (Vector a,double p){return Vector(a.x*p,a.y*p);} 2 Vector operator / (Vector a,double p){return Vector(a.x/p,a.y/p);} 3 inline Vector Divide_Point(Point a,Point b,double p1,double p2){return (a*p1+b*p2)/(p1+p2);}//A,B分点 4 inline Vector Cross_Point(Point a,Point b,Point c,Point d) 5 {return Divide_Point(a,b,Cross(d-a,c-a),Cross(c-b,d-b));}//直线交点
扩展:如果求两条线段的交点呢?
这时我们就要判断交点是否在AB,CD上了。我们可以通过判断OA、OB向量的点积,以及OC、OD向量的点积来确定:如果O在两线段上,那么两个点积都是负的。
例4:给出n边形的n个顶点(x1,y1)……(xn,yn),求一个给定点是否在多边形内。
一般来说,判断这个的方法有多种,比如引一条射线看与边的交点个数,算夹角之和是否等于360°,算叉积是否都为负,等等。
但是,我们还有另外一种logn求某个点是否在凸多边形(如果是凹多边形,这个方法就不再适用,较为推荐的是引线法)内部的方法,并且比较稳定
首先,我们把n边形分为n-2个三角形,那么如果某个点在多边形内部。
接着,我们通过叉积计算这个点到底在哪个区间。判断的方法很好想,不再赘述。
最后,我们得到了这个点可能处在的区间,然后我们判断这个点是否在多边形那条边的“左侧”(使用叉积判断)即可
代码大概长这样(所有点已经按照逆时针排好序)
1 inline bool judge(Point x) 2 { 3 p[n+1]=p[1];//编号1~n,处理边界 4 //判断多边形为线段时是否在线段上,视情况添加这段代码 5 /*if(n==2) 6 { 7 if(Dot(p[1]-x,p[2]-x)==-length(p[1]-x)*length(p[2]-x))return 1; 8 else return 0; 9 }*/ 10 int l=2,r=n,ans=-1; 11 while(l<=r) 12 { 13 int mi=(l+r)>>1; 14 if(Cross(p[mi]-p[1],x-p[1])>eps)ans=mi,l=mi+1; 15 else r=mi-1; 16 } 17 if(ans==-1)return 0; 18 if(Cross(p[ans+1]-p[ans],x-p[ans])>eps)return 1; 19 }
关于向量部分的基础内容暂时就这么多,以后我还会带来其他计算几何的知识。希望看完博文的你有所收获:)


 浙公网安备 33010602011771号
浙公网安备 33010602011771号