[您有新的未分配科技点][BZOJ3545&BZOJ3551]克鲁斯卡尔重构树
这次我们来搞一个很新奇的知识点:克鲁斯卡尔重构树。它也是一种图,是克鲁斯卡尔算法求最小生成树的升级版首先看下面一个问题:BZOJ3545 Peaks。
在Bytemountains有N座山峰,每座山峰有他的高度h_i。有些山峰之间有双向道路相连,共M条路径,每条路径有一个困难值,这个值越大表示越难走。
现在有Q组询问,每组询问询问从点v开始只经过困难值小于等于x的路径所能到达的山峰中第k高的山峰,如果无解输出-1。N<=1e5,M,Q<=5*1e5
上面这个题没有要求在线,因此我们可以离线构造最小生成树,然后当小于等于一个询问的困难值的所有边都加入后,就可以查询当前的询问点。
这种操作只需要主席树上树+启发式合并就可以解决了。(参考资料:主席树上树http://www.cnblogs.com/LadyLex/p/7275164.html,启发式合并http://www.cnblogs.com/LadyLex/p/7275793.html)
但是如果强制在线呢?BZOJ3551 Peaks加强版,在上一题基础上强制在线。
可以用来解决一系列“查询从某个点出发经过边权不超过val的边所能到达的节点”的问题,可以和其他数据结构(比如主席树)套用来维护更加复杂的询问。
克鲁斯卡尔重构树的核心思想是,当添加最小生成树中的边的时候,不在两个点间直接加边,而是新建节点,让边的两个端点所在的联通块的代表点分别作为它的左右儿子节点,然后这个新建的点,就成为这整个连通块的代表点,点权为连边的值(最开始n个叶子节点点权为0)。比如看下面这张图:首先连接(1,2),新建一个点5。再连接(3,4),新建一个点6。然后连接(1,3),连接它们各自联通块的代表点(5,6),再新建一个点7。
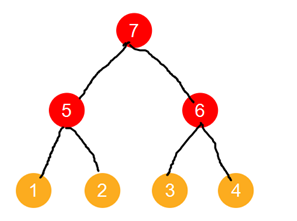
这样得到的树有一个很优雅的性质:一个点的所有子树节点的权值都小于等于它的权值,并且从它开始逐渐向子节点移动,权值是单调不上升的。这个性质是显然的,因为我们在构造树的时候是从小到大插入的边,因此父亲节点的权值一定大于等于子节点的值。
查询时,首先可以在树上倍增得到当前查询点所能够到达的最远的祖先点,那么从这个点能够到达的符合边权限制条件的连通块中的节点,就是祖先点的子树中所有的叶节点。
然后我们按dfs序维护一个主席树上树就可以解决了。
代码见下:
1 #include <cstring> 2 #include <cstdio> 3 #include <algorithm> 4 #include <ctime> 5 using namespace std; 6 const int N=100100; 7 int h[N*2],val[N*2],n,tot,num,cnt,stack[N],e,adj[N*2]; 8 int f[N*2][20],bin[25],fa[N*2],l[N*2],r[N*2]; 9 struct edge{int qi,zhong,val;}intn[N*5]; 10 struct link{int zhong,next;}s[N*2]; 11 inline void mission1(int rt){for(int i=1;bin[i]<=n;i++)f[rt][i]=f[f[rt][i-1]][i-1];} 12 inline void add(int qi,int zhong){s[++e].zhong=zhong;s[e].next=adj[qi];adj[qi]=e;} 13 inline bool mt(const edge &a,const edge &b){return a.val<b.val;} 14 int find(int a){return (fa[a]==a)?a:fa[a]=find(fa[a]);} 15 struct node 16 { 17 int cnt;node *ch[2]; 18 node(){cnt=0;ch[0]=ch[1]=NULL;} 19 inline void update(){cnt=ch[0]->cnt+ch[1]->cnt;} 20 }*null=new node(),*root[2*N]; 21 inline node* newnode(){node *o=new node();o->ch[0]=o->ch[1]=null;return o;} 22 void insert(node *&o,node *old,int l,int r,int pos) 23 { 24 o->cnt=old->cnt+1; 25 if(l==r)return; 26 int mi=(l+r)>>1; 27 if(pos<=mi)o->ch[1]=old->ch[1],o->ch[0]=newnode(),insert(o->ch[0],old->ch[0],l,mi,pos); 28 else o->ch[0]=old->ch[0],o->ch[1]=newnode(),insert(o->ch[1],old->ch[1],mi+1,r,pos); 29 o->update(); 30 } 31 inline int query(int a,int x,int k) 32 { 33 int le=1,ri=tot; 34 for(int j=18;~j;j--) 35 if(f[a][j]&&val[f[a][j]]<=x)a=f[a][j]; 36 node *a1=root[r[a]],*a2=root[l[a]-1]; 37 if(a1->cnt-a2->cnt<k)return -1; 38 while(le<ri) 39 { 40 int tmp=a1->ch[1]->cnt-a2->ch[1]->cnt,mi=(le+ri)>>1; 41 if(tmp>=k)a1=a1->ch[1],a2=a2->ch[1],le=mi+1; 42 else a1=a1->ch[0],a2=a2->ch[0],k-=tmp,ri=mi; 43 } 44 return stack[ri]; 45 } 46 void dfs(int rt) 47 { 48 mission1(rt);l[rt]=++num; 49 if(rt<=n)insert(root[num],root[num-1],1,tot,h[rt]); 50 else root[num]=root[num-1]; 51 for(int i=adj[rt];i;i=s[i].next)dfs(s[i].zhong); 52 r[rt]=num; 53 } 54 int main() 55 { 56 int m,q,ans=0,v,x,k;scanf("%d%d%d",&n,&m,&q); 57 bin[0]=1;for(int i=1;i<=22;i++)bin[i]=bin[i-1]<<1; 58 null->ch[0]=null->ch[1]=null; 59 for(int i=1;i<=n*2;i++)fa[i]=i; 60 for(int i=1;i<=n;i++)scanf("%d",&h[i]),stack[i]=h[i]; 61 for(int i=1;i<=m;i++)scanf("%d%d%d",&intn[i].qi,&intn[i].zhong,&intn[i].val); 62 sort(stack+1,stack+n+1); 63 tot=unique(stack+1,stack+n+1)-stack-1; 64 for(int i=1;i<=n;i++)h[i]=lower_bound(stack+1,stack+tot+1,h[i])-stack; 65 sort(intn+1,intn+m+1,mt);cnt=n; 66 for(int i=1;i<=m;i++) 67 { 68 int u=find(intn[i].qi),v=find(intn[i].zhong); 69 if(u!=v) 70 { 71 val[++cnt]=intn[i].val,fa[u]=fa[v]=cnt; 72 add(cnt,u),add(cnt,v),f[u][0]=f[v][0]=cnt; 73 if(cnt-n==n-1)break; 74 } 75 } 76 for(int i=0;i<=cnt;i++)root[i]=newnode(); 77 for(int i=1;i<=cnt;i++)if(!l[i])dfs(find(i)); 78 while(q--) 79 { 80 scanf("%d%d%d",&v,&x,&k); 81 if(ans!=-1)v^=ans,x^=ans,k^=ans;/*去掉这句强制在线可以ACbzoj3545*/ 82 printf("%d\n",ans=query(v,x,k)); 83 } 84 }
克鲁斯卡尔重构树是个比较小众的知识点,但在处理对口的操作时十分强大。下次你再看到类似询问的时候,不妨想一想克鲁斯卡尔重构树,也许就会柳暗花明又一村:)


 浙公网安备 33010602011771号
浙公网安备 33010602011771号