2021.03.06【NOIP提高A组】模拟
2021.03.06【NOIP提高A组】模拟
T1:5426. 【NOIP2017提高A组集训10.25】摘Galo
我在考试时就想到了正解,只不过打的太丑而超时了,具体原因:我在dfs时不断做着memset(bz,0,sizeof,bz);。。。然后GG;;;正解2.OvO 题目对取 Galo 的要求,即不能同时取一对祖先和子孙。我们可 以在 DFS 序上 DP。对于选择取 Galo[i]的决策,即选择了 DFS 序上 i 号节点的子树所对应的区间。只要选择的区间不相交、不重复,则 是一个合法的取法。这样,题目就成了一个区间覆盖 DP 问题,复 杂度 O(n*k)。我的代码太丑就不放了,避免你们也超时/emoji😆
T2 5438. 【NOIP2017提高A组集训10.31】Tree
这道题特别水,考场就有一堆人切了,正解:你只要判断儿子和父亲的颜色是否相同若不同则把儿子加入答案,最后看root是否为白色就行了
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
int i,j,n,m,k,l,e[2000001][2],h[2000001],color[600001],x,y,ans[600001],num,tot,z[1000001];
void add(int u,int v)
{
e[++tot][0]=h[u];
e[tot][1]=v;
h[u]=tot;
}
int main()
{
freopen("tree.in","r",stdin);
freopen("tree.out","w",stdout);
scanf("%d",&n);for(i=1;i<=n;i++) scanf("%d",&color[i]);
for(i=1;i<n;i++)
{
scanf("%d%d",&x,&y);
add(x,y);
}
z[++z[0]]=1;
while(z[0]>0)
{
x=z[z[0]];
for(i=h[x];i;i=e[i][0])
{z[++z[0]]=e[i][1];if(color[e[i][1]]!=color[x]) ans[++num]=e[i][1];}
h[x]=0;
if(x==z[z[0]]) z[0]--;
}
if(color[1]!=0) ans[++num]=1;
sort(ans+1,ans+1+num);
for(i=1;i<=num;i++) printf("%d ",ans[i]);
return 0;
}
注意打dfs的要打人工栈。。
T3 5427. 【NOIP2017提高A组集训10.25】吃草
考试时只会50分的。。。对于第一个问题是可以很轻松地解决
用贪心的思想,就是按照端点来排序,能放在同一个就放在同一个集合里面。
对于第二个问题我们发现ans=|(l+r)-x|*2; 就对于一个区间其实就是中间点与选的位置的差距的两倍;
知道这个后,我们要求的不过是一堆中间点与你选的位置的差距的最小值而已。
我们设f[i]表示在1~i所放的最少羊的个数,其中强制i必放。g[i]表示在f[i]下的最小距离;
首先我们知道f[i]一定是单调递增的,而且 对于i我们枚举一个j转移时,必须保证j~i中的所有区间不存在 j<l<=r<i;这样你就无法从f[j]+1---->f[i] 这种情况你就需要多拿几只羊出来了,这也是个小剪枝。。。
然后就是转移g了。显然我们可以把中心点在[j,mid]的全用j羊解决,(mid,i]的用i羊解决,然后用一个前缀和,处理每一个区间就行了,(就比如:[j,mid]中所有中心点的和减去i*[j,mid]中的个数。。。。剩下自己思考)然后就没了。。。。。。注意统计答案时还要计算最后一个羊之后中心点的答案
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
const int N=300002;
struct nup {long long l,r;}a[N];
long long i,j,n,m,k,t,l,r,c[N],y1,z,x,y,num,z1,tot,kk,mi,b[N],f[N],g[N],ma,num1[N],qz1[N],ans,mii,maa,mx;
bool cmp(nup x,nup y){return x.l<y.l;}
bool cmp1(nup x,nup y){return x.r<y.r;}
long long abss(long long x){return(x>0?x:-x);}
long long max(long long a,long long b){return a>b?a:b;}
long long min(long long a,long long b){return a<b?a:b;}
inline long long read(){
long long x=0,f=1;char ch=getchar();
while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}
while(ch>='0'&&ch<='9'){x=(x<<1)+(x<<3)+(ch^48);ch=getchar();}
return x*f;
}
int main()
{
freopen("grass.in","r",stdin);
freopen("grass.out","w",stdout);
n=read();t=read();mi=987654321;
for(i=1;i<=n;i++) a[i].l=read(),a[i].r=read(),c[a[i].r]--,mi=min(mi,a[i].l),b[i]=(a[i].l+a[i].r)/2;
sort(b+1,b+1+n);
sort(a+1,a+1+n,cmp);
x=a[1].l;y=1;
while(x<=a[n].r&&y<=n)
{
z=0;tot=0;y1=y;
while(c[x]==0) x++;
while(a[y].l<=x&&a[y].r>=x&&y<=n)
{
if((a[y].l+a[y].r-1)/2<x) tot++;
else tot--;
z=max(z,a[y].l),c[a[y].r]++,y++;
}
num++;x=a[y].l;
}
printf("%lld\n",num);
if(t==1)
{
sort(a+1,a+1+n,cmp1);
mi=mii=987654321000000;ma=maa=0;
for(i=1;i<=n;i++) qz1[b[i]]+=b[i],mi=min(mi,b[i]),ma=max(ma,b[i]),num1[b[i]]++,mii=min(mii,a[i].l),maa=max(maa,a[i].r);
for(i=1;i<=maa;i++) qz1[i]+=qz1[i-1],num1[i]+=num1[i-1],g[i]=-1;
for(i=1;i<=maa;i++)
{
for(;x<=n&&a[x].r<i;x++)mx=max(mx,a[x].l);
for(j=mx;j<i;j++)
{
if(f[i]==0||(f[j]+1<=f[i]))
{
int mid=(i+j)/2;
if(f[j]+1<f[i]) g[i]=-1;
f[i]=f[j]+1;
if(f[i]!=1)
{
if(g[i]!=-1) g[i]=min(g[i],1LL*(g[j]+qz1[mid]-qz1[j-1]-(num1[mid]-num1[j-1])*j*1LL)+1LL*(1LL*i*(num1[i]-num1[mid])-(qz1[i]-qz1[mid])));
else g[i]=1LL*(g[j]+qz1[mid]-qz1[j-1]-(num1[mid]-num1[j-1])*j*1LL)+1LL*(1LL*i*(num1[i]-num1[mid])-(qz1[i]-qz1[mid]));
}
else
{
if(g[i]!=-1) g[i]=min(g[i],(i*num1[i]-qz1[i]));
else g[i]=(i*num1[i]-qz1[i]);
}
}
}
}
mi=0;ans=987654321000000;
for(;x<=n;x++)mx=max(mx,a[x].l);
for(int i=mx;i<=maa;i++)
if(f[i]==num)ans=min(ans,g[i]+qz1[maa]-qz1[i-1]-(num1[maa]-num1[i-1])*i);
printf("%lld",ans*2);
}
}
T4 5439. 【NOIP2017提高A组集训10.31】Calculate
就推柿子。。
因为A范围很小,所以我们就把A归类,同样数字的归为一类,比如A={1,1,1,3,4,4,5,}
我们就可以处理x=1时,x=3时......
那么原来的式子就变成了
那么我们考虑设g[i]=b[i]%x,即按照a[i]来分组,在设在k个数中有t个数的g要大于T%x.(这个用桶)
那么有: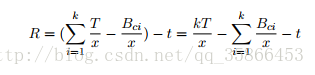
然后预处理出后面那两个东西就可以了。
#pragma GCC optimize(2)
#pragma GCC optimize(3,"Ofast","inline")
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
struct nup {int a,b,id,qz;}f[400001];
long long n,m,k,t,op,x,y,num,kk,zz[400001],tot,g[400001],mid,l,r,G[400001],F[2001][2001];
bool cmp(nup x,nup y){return(x.a==y.a?(x.b>y.b):x.a<y.a);}
inline long long pd(long long T)
{
long long res=0,i=0;
for(register int i=1;i<=502;++i)
{
res+=F[i][i]*(T/i)-G[i];
res+=-F[i][i]+F[i][T%i];
}
return res;
}
inline long long read(){
long long x=0,f=1;
char ch=getchar();
while(ch<'0'||ch>'9'){
if(ch=='-')
f=-1;
ch=getchar();
}
while(ch>='0'&&ch<='9'){
x=(x<<1)+(x<<3)+(ch^48);
ch=getchar();
}
return x*f;
}
int main()
{
freopen("calculate.in","r",stdin);
freopen("calculate.out","w",stdout);
scanf("%lld",&t);
while(t>0)
{
n=read();m=read();
memset(G,0,sizeof G);memset(F,0,sizeof F);
for(register int i=1;i<=n;++i) f[i].a=read();
for(register int i=1;i<=n;++i) f[i].b=read();
for(register int i=1;i<=n;++i) G[f[i].a]+=f[i].b/f[i].a,F[f[i].a][f[i].b%f[i].a]++;
for(register int i=1;i<=502;++i)
for(register int j=1;j<=i;++j) F[i][j]+=F[i][j-1];
for(register int i=1;i<=m;++i)
{
op=read();
if(op==1)
{
x=read();y=read();
G[f[x].a]-=f[x].b/f[x].a;
for(register int j=f[x].b%f[x].a;j<=f[x].a;++j) F[f[x].a][j]--;
f[x].a=y;
G[f[x].a]+=f[x].b/f[x].a;
for(register int j=f[x].b%f[x].a;j<=f[x].a;++j) F[f[x].a][j]++;
}
else if(op==2)
{
x=read();y=read();
G[f[x].a]+=y/f[x].a-f[x].b/f[x].a;
long long l=f[x].b%f[x].a,r=y%f[x].a;
if(l<=r) for(register int j=l;j<r;++j) F[f[x].a][j]--;
else for(register int j=r;j<l;++j) F[f[x].a][j]++;
f[x].b=y;
}
else
{
k=read();
l=1;r=f[1].a*k+f[1].b+f[2].b+f[2].a*k;
while(l<r)
{
mid=(l+r)/2;
long long cnt=pd(mid);
if(cnt>=k) r=mid;else l=mid+1;
}
printf("%lld\n",l);
}
}
t--;
}
}

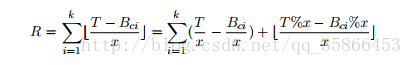

 浙公网安备 33010602011771号
浙公网安备 33010602011771号