虚树 入门

虚树：个人认为是一种将一颗大树浓缩成一颗小树的神奇操作。（每一次询问时只有一些关键点是有用的，别的点可以省略.）

虚树的主要思想是：对于一棵树，仅仅保留有用的点，重新构建一棵树。这里有用的点指的是询问点和它们的LCA例如

 

 

 这是处理过后的树.

最暴力的方法是每次暴力枚举LCA但是会超时........ 这里是用单调栈。

具体做法（粗略）

首先我们在栈中添加节点 ，然后接下来按照 DFS 序从小到大添加关键节点。假如当前的节点与栈顶节点的 LCA 就是栈顶节点的话，则说明它们是在一条链上的。所以直接把当前节点入栈就行了。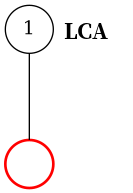

假如当前节点与栈顶节点的 LCA 不是栈顶节点的话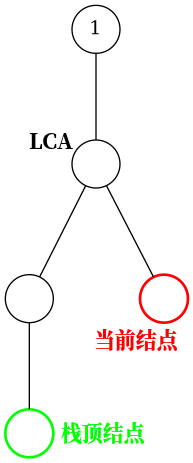：这时，当前单调栈维护的链是：而我们需要把链变成

那么我们就把蓝色结点弹栈即可，在弹栈前别忘了向它在虚树中的父亲连边。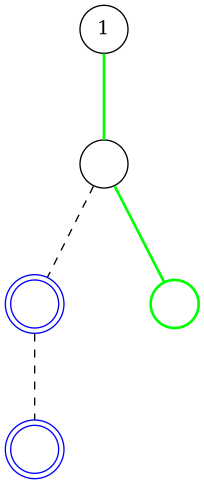

inline bool cmp(const int x, const int y) { return id[x] < id[y]; }

void build() {
  sort(h + 1, h + k + 1, cmp);
  sta[top = 1] = 1, g.sz = 0, g.head[1] = -1;
  // 1 号节点入栈，清空 1 号节点对应的邻接表，设置邻接表边数为 1
  for (int i = 1, l; i <= k; ++i)
    if (h[i] != 1) {
      //如果 1 号节点是关键节点就不要重复添加
      l = lca(h[i], sta[top]);
      //计算当前节点与栈顶节点的 LCA
      if (l != sta[top]) {
        //如果 LCA 和栈顶元素不同，则说明当前节点不再当前栈所存的链上
        while (id[l] < id[sta[top - 1]])
          //当次大节点的 Dfs 序大于 LCA 的 Dfs 序
          g.push(sta[top - 1], sta[top]), top--;
        //把与当前节点所在的链不重合的链连接掉并且弹出
        if (id[l] > id[sta[top - 1]])
          //如果 LCA 不等于次大节点（这里的大于其实和不等于没有区别）
          g.head[l] = -1, g.push(l, sta[top]), sta[top] = l;
        //说明 LCA 是第一次入栈，清空其邻接表，连边后弹出栈顶元素，并将 LCA 入栈
        else
          g.push(l, sta[top--]);
        //说明 LCA 就是次大节点，直接弹出栈顶元素
      }
      g.head[h[i]] = -1, sta[++top] = h[i];
      //当前节点必然是第一次入栈，清空邻接表并入栈
    }
  for (int i = 1; i < top; ++i)
    g.push(sta[i], sta[i + 1]);  //剩余的最后一条链连接一下
  return;

作者不易，，，ε=(´ο｀*)))唉，，，

转载请附上链接Thanks♪(･ω･)ﾉ