二分图及其应用
二分图及其应用
二分图(Bipartite Graph),又称二部图,是一个比较重要的考点,在竞赛中占了一定的比例。
定义
二分图的定义是:若一个图\(G=<V,E>\)的顶点集\(V\)可分割为两个互不相交的子集\(X\)(称为左部)和\(Y\)(称为右部),并且边集\(E\)中的每条边所关联的两个顶点分别属于\(X\)和\(Y\)两个集合,则图\(G\)为二分图。
一个图\(G\)为二分图的充要条件是图中没有奇环(长度为奇数的环)。
二分图判定
由二分图的充要条件推出一个判定方法:染色法,具体算法如下:
任意选取一个点,染为黑色,然后DFS每个节点,将每次遍历到的节点染成与上个节点不同的颜色,上个节点为白色则该点为黑色,上个节点为黑色则该点为白色。若染色时产生矛盾,则此图不是二分图;若遍历了整个图都没有矛盾产生,则此图是二分图。
vector<int>g[N];//vector存图
int n,m,vis[N],col[N],ans=1;
//col[i]表示i的颜色,0为黑色,1为白色,-1为未染色
//搜索前,将col[]全部初始化为-1,col[根节点]设为0
bool dfs(int u)
{
vis[u]=1;//如果原图不一定连通,则对每个连通块分别判定
for(int i=0,v;i<g[u].size();i++)
{
v=g[u][i];
if(col[u]==col[v])
return false;
if(col[v]==-1)
{
col[v]=!col[u];
if(!dfs(v))
return false;
}
}
return true;
}
for(int i=1;i<=n;i++)
{
memset(col,-1,sizeof(col)),col[i]=0;
if(!vis[i])
ans&=dfs(i);
}
二分图最大匹配
定义与性质
一个任何两条边都没有公共端点的边集称为为图的一组匹配(matching)或边独立集(edge independet set)。边数最多的匹配称为二分图的最大匹配。
匹配了二分图中较小集合(\(X\),\(Y\)中小的一个)的匹配称为完备匹配或完全匹配(complete matching),匹配了所有点的匹配称为完美匹配(perfect matching)。
属于匹配\(M\)的边称为匹配边,其余为非匹配边。匹配边的端点称为匹配点,其余为非匹配点。
若一条路径\(P\)连接两个非匹配点,且匹配边和非匹配边在\(P\)上交错出现,那么称\(P\)是\(M\)的一条增广路(augmenting path)。
显然,若我们将匹配\(M\)中的一条增广路\(P\)上的匹配边变为非匹配边,非匹配边变为匹配边(这个操作称为路径取反),可得一个更大的匹配\(M'\),且匹配数增加\(1\)。
推论
二分图的一组匹配\(M\)是最大匹配,当且仅当图中不存在相对于\(M\)的增广路
算法
匈牙利算法
由这个推论可以得到一个“增广路算法”,即以DFS为框架,遍历图中的每个点并不断增广,直到找不到增广路为止。
该算法就是著名的匈牙利算法。现在来看它的具体过程:
- 设\(M=\varnothing\)。即所有边均为非匹配边。
- 寻找增广路\(P\)。给当前节点\(x\)寻找匹配点\(y\),回溯时进行路径取反,得到更大的匹配\(M'\)
- 重复第2步,直到找不到增广路(即发现所有节点都被搜索过了)为止。
对于左部点\(x\)那么如何寻找匹配点\(y\)?
经过分析可发现,点y能为匹配点的两个条件是:
- \(y\)为非匹配点。
此时\(x\)~\(y\)是一条增广路。
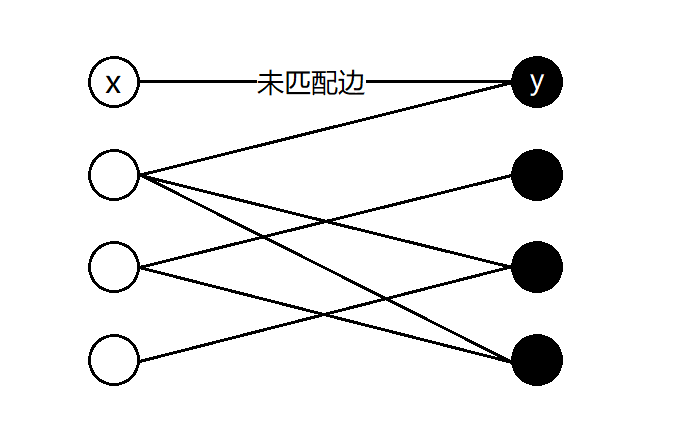
- \(y\)已与\(x'\)匹配,但又有\(y'\)能与\(x'\)匹配。
此时\(x\)$y$\(x'\)~\(y'\)是一条增广路。
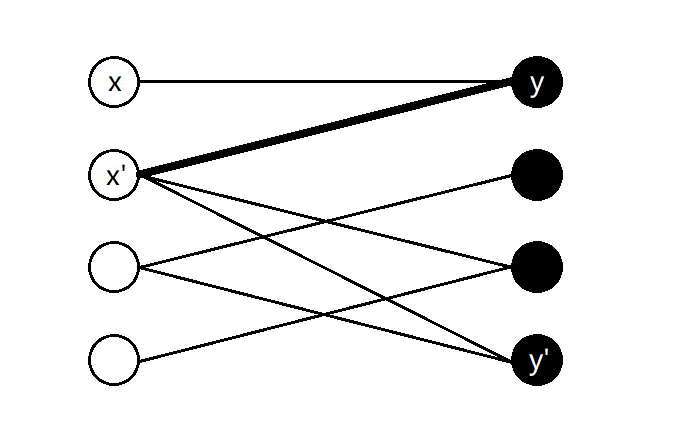
另外在这种情况中,还可能出现我们找到的\(y'\)已经匹配的情况。
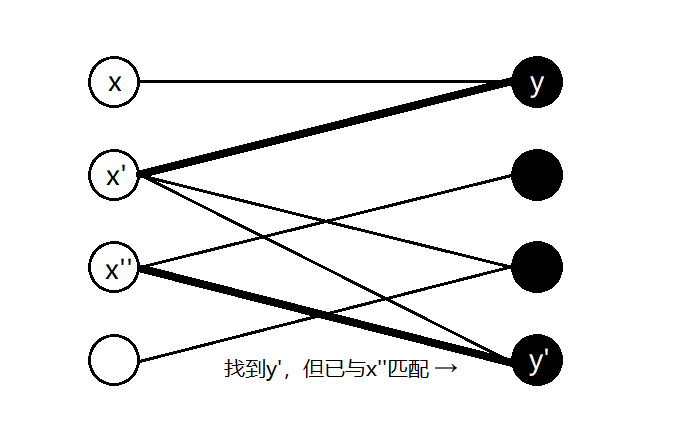
这是一个子问题,我们对\(x'\)递归处理(这也是要采用DFS作为搜索框架的原因)
有了以上分析,我们就可以写代码了。
时间复杂度\(O(nm)\)。
模板题代码:
#include<iostream>
#include<algorithm>
#include<string>
#include<cstdio>
#include<cstdlib>
#include<cstring>
#define N 1005
#define M 50005
using namespace std;
struct edge{
int nxt,to;
}e[M<<1];
int n,m,e0,tot,head[N],vis[N],match[N],ans;
void addedge(int x,int y)
{
e[++tot]=(edge){head[x],y};
head[x]=tot;
}
bool dfs(int x)
{
//用标记数组vis判重,避免重复搜索
for(int i=head[x],y;i;i=e[i].nxt)
if(!vis[y=e[i].to])
{
vis[y]=1;
if(!match[y]||dfs(match[y]))//y点未匹配,或从y点能找到增广路
{
match[y]=x;//路径取反
return true;//成功找到一条增广路,返回1
}
}
return false;//从x出发能搜索到的所有点都被搜索过了,找不到新的增广路,返回0
}
int main()
{
ios::sync_with_stdio(0);
cin>>n>>m>>e0;
for(int i=1,u,v;i<=e0;i++)
cin>>u>>v,addedge(u,v+n);
for(int i=1;i<=n;i++)
{
memset(vis,0,sizeof(vis));
if(dfs(i)) ans++;
}
cout<<ans<<endl;
exit(0);
}
网络最大流
利用网络流的思想,我们可以做到时间复杂度\(O(m\sqrt n)\)。
具体做法如下:
新建超级源点S与超级汇点T,从S向左部点连接有向边,从右部点向T连接有向边,网络中每条边的容量设为1。
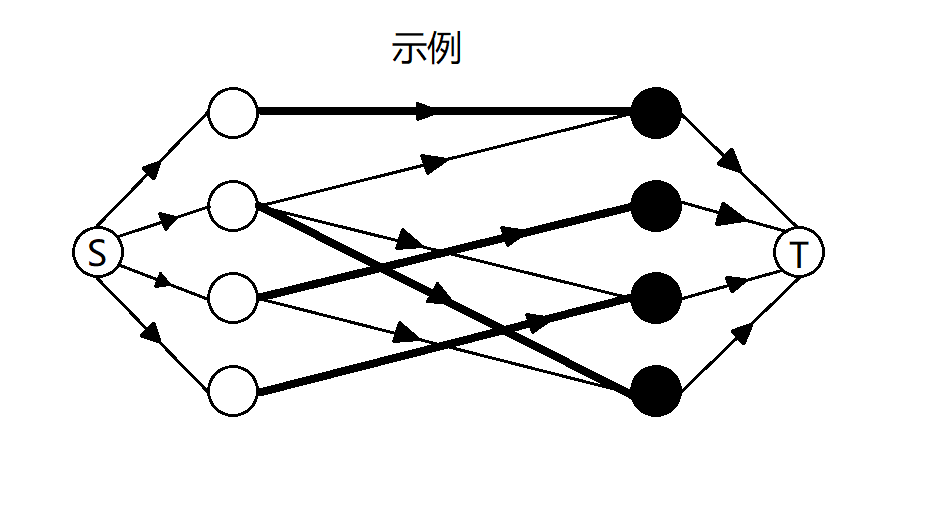
然后使用Dinic算法求出最大流即为最大匹配数,流经过的点与边就是匹配点和匹配边。
另外,有一种名为Hopcroft-Karp的算法也能做到\(O(m\sqrt n)\)的时间复杂度。