JZOJ 3945. 【湖南省队集训2014】Jabberwocky（线段树+双向链表）

JZOJ 3945. 【湖南省队集训2014】Jabberwocky

题目

Description

Input

Output

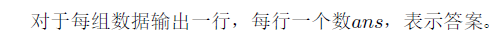
Sample Input

1
10 3
1 2 3
2 1 1
2 4 2
3 5 3
4 4 2
5 1 2
6 3 1
6 7 1
7 2 3
9 4 2

Sample Output

5

Data Constraint

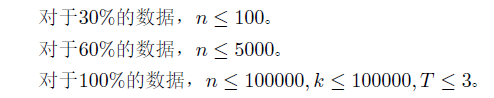
题解

• 因为要考虑线段以上和线段一下的，同时做不是很方便，所以先做一遍，把纵坐标取反后再做一遍。
• 先用双向链表将左右相邻的同颜色的点连起来，把每个点按横坐标加入线段树（或树状数组）中，
• 然后从上往下枚举线段的高度，每到一个点就先把它从线段树中删去，然后用链表找到它向左向右第一个同色的两个点（或边界），那么当前能找到最大的答案就在这两个点之间，在线段树上找到它们之间的点的个数更新答案，
• 当然，要注意这些点是不包括最左右端的两个点以及横坐标和它们相同的点的，具体做法是按横坐标排序后，将左边的点往右跳，直到第一个横坐标大于它的，且将右边的点往左跳，方法类似，最后在线段树上统计的就是跳完的两个点之间的点数。
• 题目还有一些值得注意的地方（简称坑）：
• 有可能这些点中$k$种颜色并不是全出现，则答案为$n$；
• 有可能最优答案存在于相邻的两个同色点之间，所以还要再统计一下。

代码

#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
#define N 100010
#define ll long long
#define maxn 4294967296
struct node
{
	ll x,y;
	int c,id;
}a[N];
int ans=0,n,k;
int la[N],le[N],ri[N],ts,pr[N],p[N];
struct
{
	int s,l,r;
}f[N*15];
int cmd(node x,node y)
{
	if(x.x<y.x) return 1;
	if(x.x>y.x) return 0;
	return x.y<y.y;
}
int cmd1(node x,node y)
{
	return x.y>y.y;
}
void add(int v,ll l,ll r,ll x,int c)
{
	if(l==r) f[v].s+=c;
	else
	{
		ll mid=(l+r)/2;
		if(x<=mid) 
		{
			if(!f[v].l) f[v].l=++ts;
			add(f[v].l,l,mid,x,c);
		}
		else
		{
			if(!f[v].r) f[v].r=++ts;
			add(f[v].r,mid+1,r,x,c);
		}
		f[v].s+=c;
	}
}
int find(int v,ll l,ll r,ll x,ll y)
{
	if(l==x&&r==y) return f[v].s;
	ll mid=(l+r)/2;
	if(y<=mid) return f[v].l?find(f[v].l,l,mid,x,y):0;
	if(x>mid) return f[v].r?find(f[v].r,mid+1,r,x,y):0;
	int t=0;
	if(f[v].l) t+=find(f[v].l,l,mid,x,mid);
	if(f[v].r) t+=find(f[v].r,mid+1,r,mid+1,y);
	return t;
}
void solve()
{
	sort(a+1,a+n+1,cmd);
	memset(la,0,sizeof(la));
	int i;
	for(i=1;i<=n;i++) 
	{
		ri[la[a[i].c]]=i;
		le[i]=la[a[i].c];
		la[a[i].c]=i;
		ri[i]=n+1;
		a[i].id=i;
	}
	for(i=1;i<=n;i++) if(ri[i]<=n)
	{
		int x=i,y=ri[i];
		while(a[x].x==a[i].x) x++;
		while(a[y].x==a[ri[i]].x) y--;
		if(y-x+1>ans) ans=y-x+1;
	}
	sort(a+1,a+n+1,cmd1);
	for(i=1;i<=n;i++) pr[a[i].id]=i;
	ts=1;
	for(i=1;i<=1500000;i++) f[i].l=f[i].r=0;
	for(i=1;i<=n;i++) add(1,1,maxn*2,a[i].x,1);
	for(i=1;i<=n;i++)
	{
		int L=le[a[i].id],R=ri[a[i].id];	
		int x=L,y=R;
		add(1,1,maxn*2,a[i].x,-1);
		ri[L]=R,le[R]=L;
		while(a[pr[x]].x==a[pr[L]].x) x=a[pr[x+1]].id;
		while(a[pr[y]].x==a[pr[R]].x) y=a[pr[y-1]].id;
		int s=find(1,1,maxn*2,a[pr[x]].x,a[pr[y]].x);
		if(s>ans) ans=s;
	}
}
ll read()
{
	ll s=0;
	char x=getchar();
	while(x<'0'||x>'9') x=getchar();
	while(x>='0'&&x<='9') s=s*10+x-48,x=getchar();
	return s;
}
int main()
{
	int tn,i;
	scanf("%d",&tn);
	while(tn--)
	{
		scanf("%d%d",&n,&k);
		for(i=1;i<=n;i++) 
		{
			a[i].x=read(),a[i].y=read(),a[i].c=(int)read();
			a[i].x+=maxn;
			p[a[i].c]=tn;
		}
		int ok=0;
		for(i=1;i<=k;i++) if(p[i]!=tn) ok=1;
		if(ok)
		{
			printf("%d\n",n);
			continue;
		}
		ans=0;
		solve();
		for(i=1;i<=n;i++) a[i].y=-a[i].y;
		solve();
		printf("%d\n",ans);
	}
	return 0;
}