向量叉积分配律简单证明
向量叉积分配律简单证明
引入
叉积
- 向量叉积即向量积 a × b a×b a×b,运算结果是一个向量,满足:
- 方向与 a a a, b b b都垂直,符合右手法则;
- 模等于 ∣ a ∣ ∣ b ∣ s i n θ |a||b|sinθ ∣a∣∣b∣sinθ,几何意义为以 a a a, b b b为邻边的平行四边形面积大小。
坐标运算
- 令 a = ( m , n ) a=(m,n) a=(m,n), b = ( p , q ) b=(p,q) b=(p,q)
- a × b a×b a×b的竖坐标 = ± ( m q − n p ) =±(mq-np) =±(mq−np)(符号遵循右手法则)
证明
- a = ( m , n ) a=(m,n) a=(m,n), b = ( p , q ) b=(p,q) b=(p,q)
- 设 a = x 1 + y 1 = ( m , 0 ) + ( 0 , n ) a=x1+y1=(m,0)+(0,n) a=x1+y1=(m,0)+(0,n), b = x 2 + y 2 = ( p , 0 ) + ( 0 , q ) b=x2+y2=(p,0)+(0,q) b=x2+y2=(p,0)+(0,q)
-
a
×
b
a×b
a×b的竖坐标
=
(
x
1
+
y
1
)
×
(
x
2
+
y
2
)
=(x1+y1)×(x2+y2)
=(x1+y1)×(x2+y2)
= x 1 × x 2 + x 1 × y 2 + y 1 × x 2 + y 1 × y 2 =x1×x2+x1×y2+y1×x2+y1×y2 =x1×x2+x1×y2+y1×x2+y1×y2
= x 1 × y 2 + y 1 × x 2 =x1×y2+y1×x2 =x1×y2+y1×x2
= ( m , 0 ) × ( 0 , q ) + ( 0 , n ) × ( p , 0 ) =(m,0)×(0,q)+(0,n)×(p,0) =(m,0)×(0,q)+(0,n)×(p,0)
= ± ( m q − n p ) =±(mq-np) =±(mq−np) - 问题来了,这里的证明过程中,第一步直接把括号拆开,相当于默认叉积具有分配律,那么这一定是对的吗?
- 很多地方都没有给出证明,所以这里考虑对叉积分配律给出简单的证明。
证明
- 已知 a a a, b b b, c c c为平面内向量,求证: a × ( b + c ) = a × b + a × c a×(b+c)=a×b+a×c a×(b+c)=a×b+a×c.
- 首先通过平移是向量起点重合,
- 从几何意义入手,需要满足以
a
,
b
a,b
a,b为邻边的平行四边形面积与以
a
,
c
a,c
a,c为邻边的平行四边形面积之和等于以
a
,
b
+
c
a,b+c
a,b+c为邻边的平行四边形面积(这里的面积可能为负值),
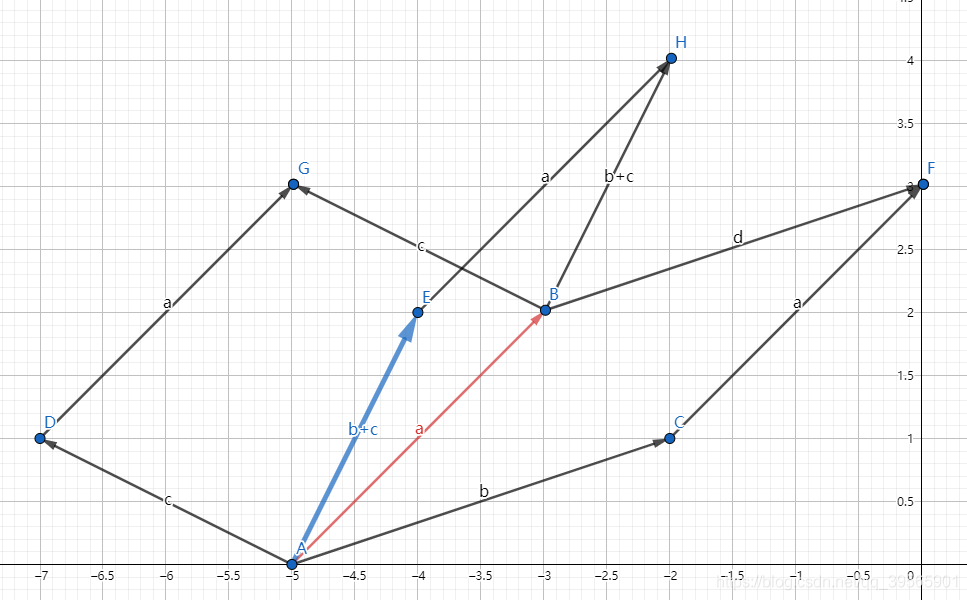
- 显然,这么看难以证明。
- 那可以把
b
b
b,
c
c
c投影到与
a
a
a垂直的直线上,令投影后的向量分别为
b
′
b'
b′,
c
′
c'
c′,如图:
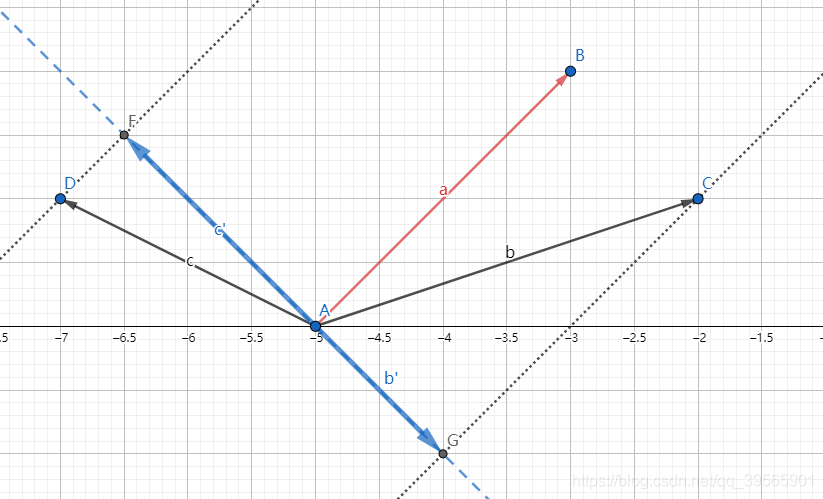
- 由叉积的几何意义易得, a × b = a × b ′ a×b=a×b' a×b=a×b′, a × c = a × c ′ a×c=a×c' a×c=a×c′
- 故
a
×
b
+
a
×
c
=
a
×
b
′
+
a
×
c
′
=
−
∣
a
∣
∣
b
′
∣
+
∣
a
∣
∣
c
′
∣
=
∣
a
∣
(
∣
c
′
∣
−
∣
b
′
∣
)
a×b+a×c=a×b'+a×c'=-|a||b'|+|a||c'|=|a|(|c'|-|b'|)
a×b+a×c=a×b′+a×c′=−∣a∣∣b′∣+∣a∣∣c′∣=∣a∣(∣c′∣−∣b′∣)
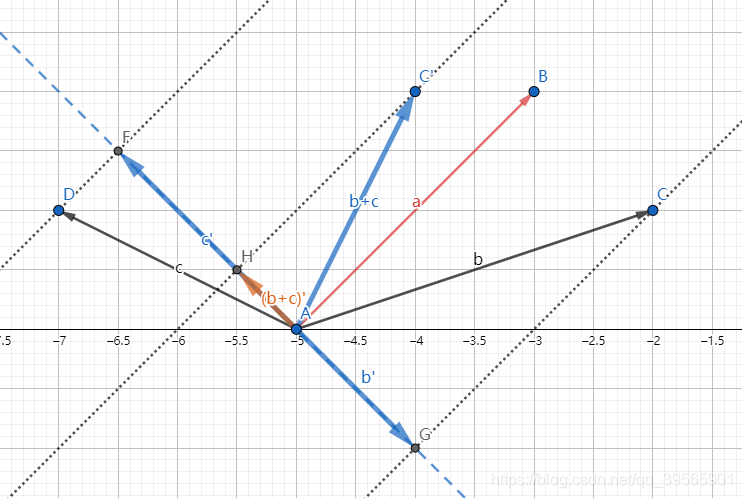
- 同理又有 a × ( b + c ) = a × ( b + c ) ′ = ∣ a ∣ ∣ ( b + c ) ′ ∣ a×(b+c)=a×(b+c)'=|a||(b+c)'| a×(b+c)=a×(b+c)′=∣a∣∣(b+c)′∣,
- 因为 ∣ c ′ ∣ − ∣ b ′ ∣ = ∣ ( b + c ) ′ ∣ |c'|-|b'|=|(b+c)'| ∣c′∣−∣b′∣=∣(b+c)′∣,所以 a × b ′ + a × c ′ = a × ( b + c ) ′ a×b'+a×c'=a×(b+c)' a×b′+a×c′=a×(b+c)′,所以 a × ( b + c ) = a × b + a × c a×(b+c)=a×b+a×c a×(b+c)=a×b+a×c,
- 得证。
- 实际上,这样就相当于把原先的三个普通平行四边形转化为了三个矩形,便于证明。
哈哈哈哈哈哈哈哈哈哈





【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· SQL Server 2025 AI相关能力初探
· Linux系列:如何用 C#调用 C方法造成内存泄露
· AI与.NET技术实操系列(二):开始使用ML.NET
· 记一次.NET内存居高不下排查解决与启示
· 探究高空视频全景AR技术的实现原理
· 阿里最新开源QwQ-32B,效果媲美deepseek-r1满血版,部署成本又又又降低了!
· 单线程的Redis速度为什么快?
· SQL Server 2025 AI相关能力初探
· AI编程工具终极对决:字节Trae VS Cursor,谁才是开发者新宠?
· 展开说说关于C#中ORM框架的用法!