JZOJ 6278. 2019.8.5【NOIP提高组A】跳房子 (分块模拟)
JZOJ 6278. 2019.8.5【NOIP提高组A】跳房子
题目
Description

Input

Output

Sample Input
4 4
1 2 9 3
3 5 4 8
4 3 2 7
5 8 1 6
4
move 1
move 1
change 1 4 100
move 1
Sample Output
4 2
1 3
1 4
Data Constraint
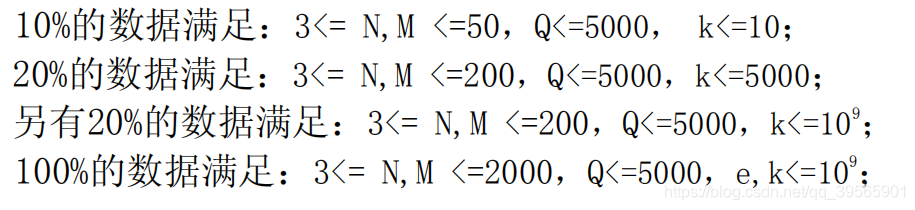
题解
- 先考虑暴力,最最暴力直接纯模拟的时间是\(O(Qk)\),得分\(20\);
- 如果考虑倍增,修改再暴力重构,得分\(30-40\);
- 但暴力重构时间太大。发现跳多了会有重复,可以记录已经经过了的点,有重复就简单的式子计算,直到每次修改才重新跳,极限复杂度\(O(Qnm)\),得分\(80\)!!!
- 这样还是慢了,据说有一种线段树维护修改和查询的方法,时间复杂度是\(O(Qn \log_2 n)\),可以过(超好写,但本人不会),但有点卡时间(实际跑得挺快的),读者可以自行思考。
- 接下来介绍正解——
- 根据最后一种暴力方法, 极限要跳\(nm\)步,若考虑类似分块的思想,计算出每\(m\)步跳到的位置,剩下的再一个个跳,修改时(巧妙的)暴力。
- 设\(to[i]\)表示\((i,1)\)跳\(m\)步后回到\((to[i],1)\),读入后先预处理出这个数组,
- 询问时先从当前的\((x,y)\)一直跳,直到跳到给出步数或\(y=1\)了退出,
- 如果还有没跳完的步数\(k\),那么还需跳\(\frac{k}{m}\)次\(m\)步和剩余的\(k\mod m\)步,
- 前面的用\(to\)数组来快速跳,同样地,记录每次跳到第一列第几行,如果有跳到重复的行,那么直接计算出答案,否则跳完为止,
- 然后剩下的再一个个跳即可。
- 重难点在于修改,
- 如果\((x,y)\)发生改变,那么\((x-1,y-1),(x,y-1),(x+1,y-1)\)跳一步的位置会有可能改变,所以能跳到它的第一列的格子的\(to\)值会可能发生改变,
- 于是对这三个点做同样的操作:
- 设该点为\((p,q)\),
- 先暴力计算出\((p,q)\)一直向后会跳到第一列第几行,记录行号\(row\),
- 接着需要把第一列能跳到\((p,q)\)的点的\(to\)值改为\(row\),
- 怎么找到这些点?
- 易得,这些点是连续的,所以一列列往回退到第一列,
- 记录\((l,r)\)表示当前列(设其为\(c\)列)的\(l-r\)行能走到\((p,q)\),考虑怎么转移到前一列
- 在\((l-1,c-1),(l,c-1),(l+1,c-1)\)中找到最小一个能跳到\((l,c)\)的,\(l\)变为其行号,
- 在\((r-1,c-1),(r,c-1),(r+1,c-1)\)中找到最大一个能跳到\((r,c)\)的,\(r\)变为其行号,
- 这样完成了区间向前一列的转移,
- 注意有可能三个位置都没法跳到\(l\)(或\(r\)),如果\(l\)和\(r\)都没法被跳到,那就退出。
- 因为\(l\)向上跳过了\(1\)会到\(n\)(\(r\)同理),所以最终的区间可能\(r<l\),或各自走了一圈又\(l≤r\)(最终会更新\([l,r]\),但实际表示的区间是\([l,n] \bigcup [1,r]=[1,n]\)),那么就变得十分复杂了。。。
- (其实是有办法解决的,用各种标记+超多判断)
- 但还有更好的办法!!!
- \(l\)如果小于\(1\)了,也不改为\(n\),让它一直变小(\(r\)同理,让它一直变大),
- 一旦\(r-l+1≥n\)了,最终区间就是\([1,n]\),
- 一旦\(r<l\)了,最终区间为空,
- 在向前反推时,\(l\)和\(r\)根据计算(\((x\mod n+n-1)\mod n+1\))转换为实际表示的\([1,n]\)中的值,但它们实际值还是不改变。
- 最终把\([l,r]\)中实际表示的每个\(i\)的\(to[i]\)改为\(row\)。
代码
#pragma GCC optimize(3)
#include<cstdio>
#include<cstring>
using namespace std;
#define N 2010
int a[N][N],q[N],p[N],bz[N],to[N],n,m;
char st[9];
int read()
{
int t=0;
char c=getchar();
while(c<'0'||c>'9') c=getchar();
while(c>='0'&&c<='9') t=t*10+c-'0',c=getchar();
return t;
}
int f(int x)
{
return (x%n+n-1)%n+1;
}
int cs(int x,int y)
{
int mx=-1,ss;
y=y%m+1;
for(int i=x-1;i<=x+1;i++)
{
int sm=a[f(i)][y];
if(sm>mx) mx=sm,ss=i;
}
return ss;
}
void change(int x,int y)
{
int u=x,v=y;
while(1)
{
u=f(cs(u,v));
v=v%m+1;
if(v==1) break;
}
int l=x,r=x;
v=y;
while(v>1)
{
v--;
int ll=1,rr=0;
for(int i=l-1;i<=l+1;i++) if(cs(i,v)>=l&&cs(i,v)<=r)
{
ll=i;
break;
}
for(int i=r+1;i>=r-1;i--) if(cs(i,v)>=l&&cs(i,v)<=r)
{
rr=i;
break;
}
if(ll>rr) return;
l=ll,r=rr;
if(r-l+1>=n)
{
l=1,r=n;
break;
}
}
for(int i=l;i<=r;i++) to[f(i)]=u;
}
int main()
{
int Q,i,j;
n=read(),m=read();
for(i=1;i<=n;i++)
for(j=1;j<=m;j++) a[i][j]=read();
scanf("%d\n",&Q);
for(i=1;i<=n;i++)
{
int x=i,y=1;
while(1)
{
x=f(cs(x,y));
y=y%m+1;
if(y==1) break;
}
to[i]=x;
}
int x=1,y=1,xx,yy,e,id=0;
while(Q--)
{
scanf("%s",st+1);
if(st[1]=='c')
{
xx=read(),yy=read(),e=read();
a[xx][yy]=e;
for(i=xx-1;i<=xx+1;i++) change(f(i),(yy+m-2)%m+1);
}
else
{
e=read();
while(y!=1)
{
x=f(cs(x,y));
y=y%m+1;
e--;
if(e==0) break;
}
int pt=e/m;
int ws=1;
q[1]=x,bz[x]=++id,p[x]=1;
while(pt--)
{
x=to[x];
if(bz[x]==id)
{
int k=p[x];
x=q[pt%(ws-k+1)+k];
break;
}
q[++ws]=x,bz[x]=id,p[x]=ws;
}
e%=m;
while(e--) x=f(cs(x,y++));
printf("%d %d\n",x,y);
}
}
return 0;
}
哈哈哈哈哈哈哈哈哈哈

