『学习笔记』并查集
并查集是一种用于解决元素分组问题的数据结构。它有两种操作:
- 合并:把两个不相交的集合合并为一个集合。
- 查询:查找两个元素是否在同一集合里。
我们可以把它理解为朋友关系:朋友的朋友是朋友。
朋友关系
比如,一共有 \(5\) 个人,分别为 \(a,b,c,d,e\)。每个人都有一个代表,即为自己的朋友之一,一个或多个人的代表需要是同一个人,遇到什么事就把锅推给代表。若一个人没有朋友,那么他的代表就是自己。
图中每个人的箭头即指向每个人的代表。

现在我们得知,\(b\) 是 \(a\) 的朋友,我们使用并查集来合并他们,并使得 \(a\) 的代表(也就是 \(a\))是他们这对朋友的代表。这里的代表可以选择 \(a\),也可以选择 \(b\)。
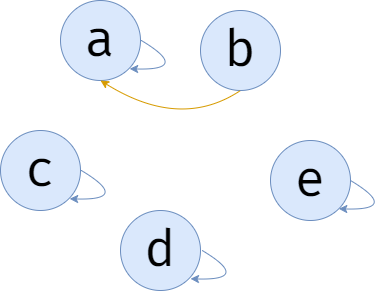
\(c\) 和 \(b\) 交朋友,我们可以使 \(c\) 的代表,也就是 \(c\),他的代表变为 \(b\)。
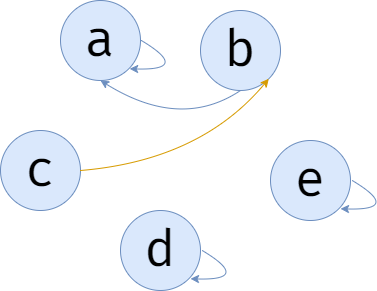
但是你会发现,它们 \(a,b,c\) 的代表不相同,\(c\) 的代表是 \(b\)。
没关系,我们可以通过 \(c\) 找到代表 \(b\),又能通过 \(b\) 找到代表 \(a\),\(a\) 的代表为自己,所以还是能够找到自己的代表的。
现在 \(d\) 和 \(e\) 又交了朋友,我们将这两个好朋友的代表选为 \(d\)。
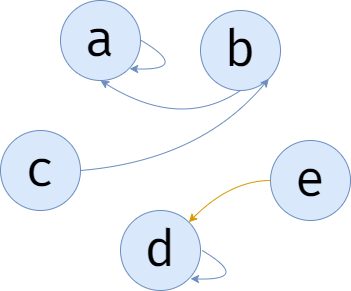
\(e\) 和 \(b\) 交了朋友,我们要让 \(e\) 的代表 \(d\),修改代表为 \(b\)。
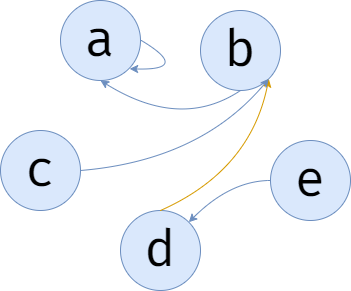
目前,所有人都有朋友关系了。
那么如何判断两个人是否有朋友关系呢?
当然是看看两个人的代表的代表的代表的代表的代表......是不是同一个人啦!
例如,我们判断 \(c\) 和 \(e\) 是否拥有朋友关系,那么就需要分别找到他们的代表的代表的代表的代表......然后判断一下是不是同一个人。

从上图可以得知, \(c\) 的代表的代表的代表的代表......是 \(a\)。
接下来找找 \(e\) 的代表的代表的代表的代表......是谁吧。
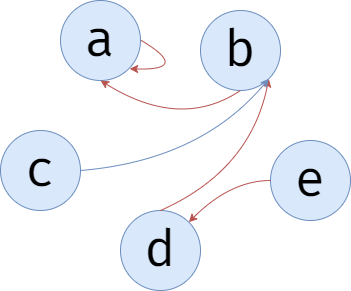
可见,\(e\) 的代表的代表的代表的代表......也是 \(a\)。
那么 \(c\) 和 \(e\) 就是好朋友啦!
代码实现
我们使用一个数组 \(f\) 来存储每个人的代表。
int f[N];
初始化
刚开始的时候,所有人的代表都要为自身。
void init(int n){ // 元素总个数 n
for(int i=1; i<=n; i++)
f[i]=i;
}
查询
这个操作,就是找到自己的代表的代表的代表的代表......了。
什么时候才停下来不再找代表,返回代表编号?
当目前找到的代表,他的代表为自身的时候,就没有继续找的必要了,那也是死循环。所以直接返回。
int find(int x){return f[x]==x ? x : find(f[x]);}
合并
在上面的演示中,我们是直接让 \(x\) 的代表的代表的代表的代表......的代表变成 \(y\) 的。
而这样做实在慢了些,如果这样合并后,要查询 \(x\) 的代表的代表的代表的代表......会怎么样?我们会先找到原来 \(x\) 的代表的代表的代表的代表......再找一遍 \(y\) 的代表的代表的代表的代表,才能找到最终的代表。
怎么样可以让他更快些呢?当然是让 \(x\) 的代表的代表的代表的代表......的代表直接变成 \(y\) 的代表的代表的代表的代表......了!
void merge(int x,int y){f[find(x)]=find(y);}
演示中的方法是这样的:
void merge(int x,int y){f[find(x)]=y;}
路径压缩优化
相信你已经注意到,我们如果多次找 \(x\) 的代表的代表的代表的代表......,那么每次最坏情况下要找 \(n\) 次代表,所以时间复杂度为 \(\mathcal{O}(n)\),显然很慢。
要是我们沿着一条路找了一遍代表,那为什么不让找过的人的代表都变成最终找到的答案呢?
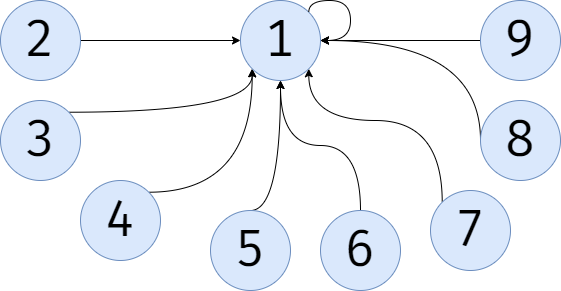
比如,有这样一个并查集:

我们要查找 \(9\) 的代表的代表的代表的代表......可见,要把所有节点都找一遍,才能找到 \(1\)。
找第一遍的时候,我们没办法,只能这样 \(\mathcal{O}(n)\) 找。可再找好几遍呢?还这么找,岂不浪费时间?
于是,我们第一遍找到答案就直接将答案放进 \(f_x\),这样也不影响整个并查集,还能加速下次查找,下次查找 \(x\) 节点,\(\mathcal{O}(1)\) 就能得出答案。
要做到这样,只需要在 find 函数中加入一点点东西:
int find(int x){return f[x]==x ? x : f[x]=find(f[x]);}
加入的就是后面的 f[x]=find(f[x]) 中的 f[x]=,这样能将路过的每个节点的答案都存下来,下次再找就只需要 \(\mathcal{O}(1)\) 了。
例如上面那个并查集,调用 find(9) 后,它长这样:
P1551 亲戚
题目大意
给你 \(n\) 个人,\(m\) 个亲戚关系,\(p\) 个询问。
如果 \(x\) 和 \(y\) 是亲戚,\(y\) 和 \(z\) 是亲戚,那么 \(x\) 和 \(z\) 也是亲戚。
对于每个询问,给定两个人的编号 \(Pi,Pj\),输出他们是否具有亲戚关系。
思路
这题的亲戚关系和上面的朋友关系很像,所以我们使用一个并查集来维护。
就拿这题来试试路径压缩优化能快多少吧!
可见,效果还是很显著的。
代码
#include <iostream>
using namespace std;
template<typename T=int>
inline T read(){
T X=0; bool flag=1; char ch=getchar();
while(ch<'0' || ch>'9'){if(ch=='-') flag=0; ch=getchar();}
while(ch>='0' && ch<='9') X=(X<<1)+(X<<3)+ch-'0',ch=getchar();
if(flag) return X;
return ~(X-1);
}
const int N=5e3+5;
int n,m,p,a,b;
template<class T=int>
class set{
public:
set(int n=1e5){f=new T[l=n+5]; clear();}
~set(){delete[] f;}
T find(T x){return f[x]==x ? x : f[x]=find(f[x]);}
void merge(T x,T y){f[find(x)]=find(y);}
void clear(){for(int i=1; i<l; i++) f[i]=i;}
private:
T *f;
int l;
};
set s;
int main(){
n=read(),m=read(),p=read();
while(m--){
a=read(),b=read();
s.merge(a,b);
}
while(p--){
a=read(),b=read();
if(s.find(a)==s.find(b)) puts("Yes");
else puts("No");
}
return 0;
}
P2078 朋友
题目大意
有两个公司 A 和 B,小明在 A 公司工作,小红在 B 公司工作。
A 公司只有男员工,编号为正数,而 B 公司只有女员工,编号为负数。
给定 A 公司的人数 \(n\) 和 \(p\) 对朋友关系,B 公司的人数 \(m\) 和 \(q\) 对朋友关系。
请你求出,小明和小红认识的人里(包括他们自己),最多能组成多少对情侣?
小明的编号为 \(1\),小红的编号为 \(-1\)。
思路
好家伙刚来一个亲戚又来一个朋友,还组情侣......
题目说了,A 和 B 公司各自内部才有朋友关系,不会有 A 公司的人与 B 公司的人有朋友关系,那么我们直接用两个并查集维护呗!
对于 B 公司的负数编号,直接转为正数即可。
然后我们统计小明和小红各自的朋友数,把公司里每个人的代表都找一遍,只要跟 \(1\) 号(也就是小明小红)的代表一样,就说明这个人是小明或小红的好朋友。
问最多能组成的情侣对数,直接输出小明和小红朋友数的最小值就可以了。
代码
#include <iostream>
using namespace std;
template<typename T=int>
inline T read(){
T X=0; bool flag=1; char ch=getchar();
while(ch<'0' || ch>'9'){if(ch=='-') flag=0; ch=getchar();}
while(ch>='0' && ch<='9') X=(X<<1)+(X<<3)+ch-'0',ch=getchar();
if(flag) return X;
return ~(X-1);
}
template<typename T=int>
inline void write(T X){
if(X<0) putchar('-'),X=~(X-1);
T s[20],top=0;
while(X) s[++top]=X%10,X/=10;
if(!top) s[++top]=0;
while(top) putchar(s[top--]+'0');
putchar('\n');
}
int n,m,p,q,x,y,ac,bc;
template<class T=int>
class set{
public:
set(int n=1e5){f=new T[l=n+5]; clear();}
~set(){delete[] f;}
T find(T x){return f[x]==x ? x : f[x]=find(f[x]);}
void merge(T x,T y){f[find(x)]=find(y);}
void clear(){for(int i=1; i<l; i++) f[i]=i;}
private:
T *f;
int l;
};
set a,b; // a 维护 A 公司,b 维护 B 公司
int main(){
n=read(),m=read(),p=read(),q=read();
while(p--) // 输入朋友关系
a.merge(read(),read());
while(q--)
b.merge(-read(),-read());
for(int i=1; i<=n; i++) // 统计朋友
ac+=a.find(i)==a.find(1);
for(int i=1; i<=m; i++)
bc+=b.find(i)==b.find(1);
write(min(ac,bc));
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号