『学习笔记』字典树
字典树(Trie)是一种用于操作字符串的树型结构,可以用来存储和查询字符串。
例如,在一棵字典树中插入 \(\texttt{iak,ioi,akly,me,fake,ccf}\) 后,这棵树长这样:

图中橙色节点为存在的字符串,必须标记一下。否则,像图中 \(\texttt{a,c,f,i,m,cc,fa,ia,io,akl,fak}\) 这些子串,都会被认为是插入的字符串。
Trie 的根节点始终为空,它的作用就是存储通向子树的边。这些边各有各的权值,都是一个字符。
那么每个节点表示的字符串即为:父节点表示的字符串,末尾添加父节点通向该节点的边权。
例如 \(\texttt{ak}\),它的父节点为 \(\texttt{a}\),通向它的边权为 \(\texttt{k}\),故这个节点的值为 \(\texttt{a}\) 的末尾加上 \(\texttt{k}\),即 \(\texttt{ak}\)。
下面来看看具体操作过程吧。
插入
插入过程中,先从根节点开始搜,搜插入字符串的第一个字符,如果第一个字符的儿子不存在,那么创建节点,并进入。否则直接进入。一直这样搜到字符串末尾,于是最后到达的节点就是要去的节点了,标记这个节点,就完成了插入过程。
例如,要在上面的字典树中插入字符串 \(\texttt{meet}\):
首先,从根节点寻找边权为第一个字符 \(\texttt{m}\) 的边,发现已有,则进入,到达 \(\texttt{m}\) 节点。
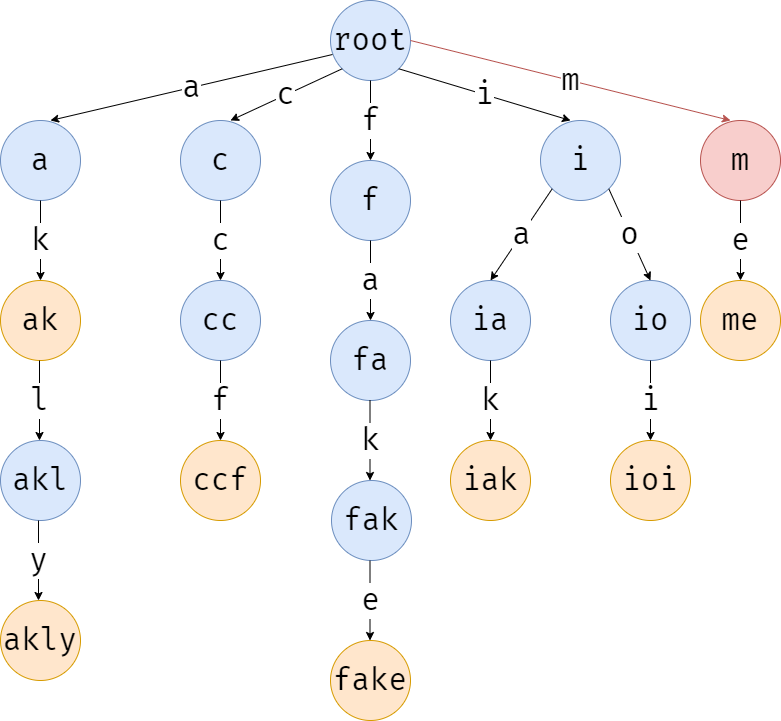
接着,寻找第二个字符 \(\texttt{e}\),还是有,进入子节点。
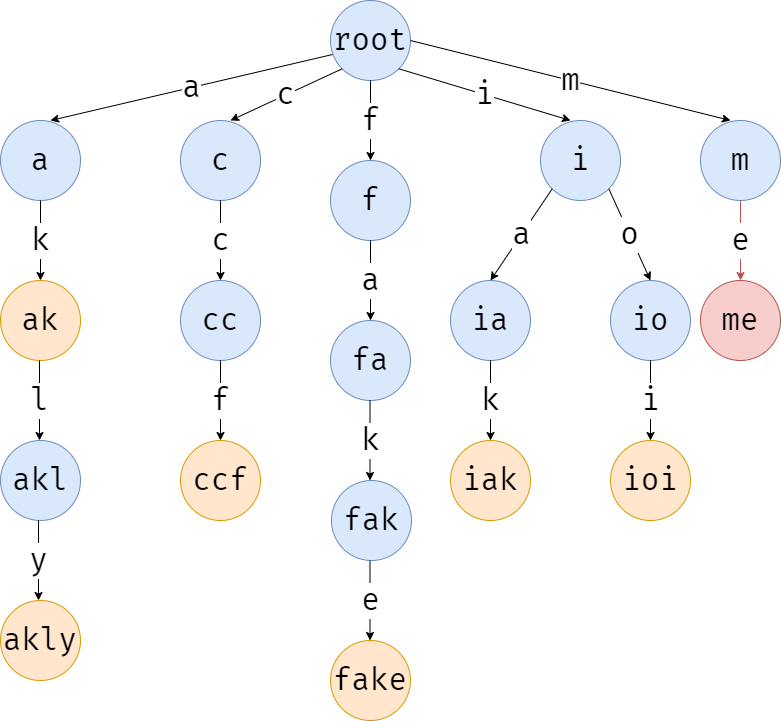
接着找第三个字符 \(\texttt{e}\),发现没有这条边,创建儿子,并进入。
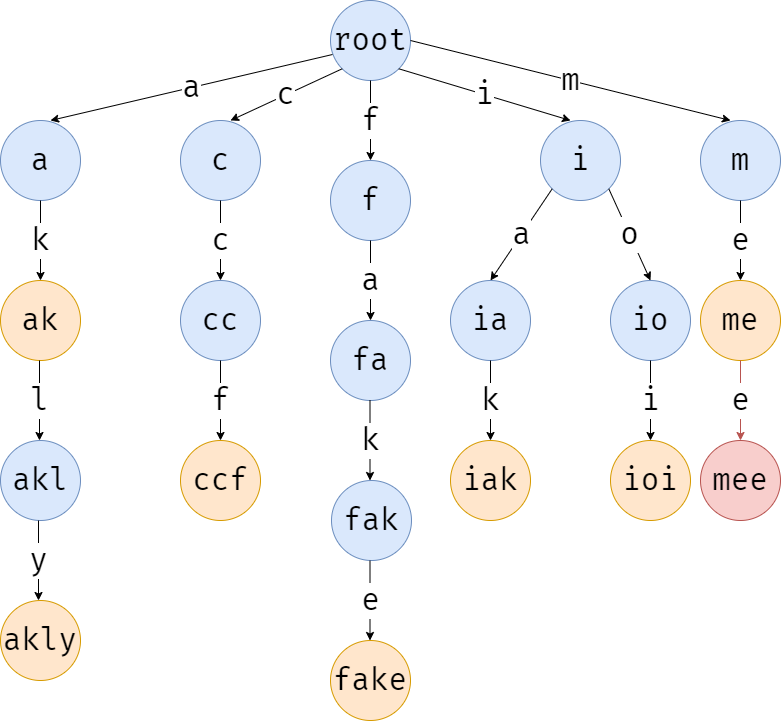
最后找最后一个字符 \(\texttt{t}\),\(\texttt{mee}\) 节点同样没有权值为 \(\texttt{t}\) 的出边,创建。
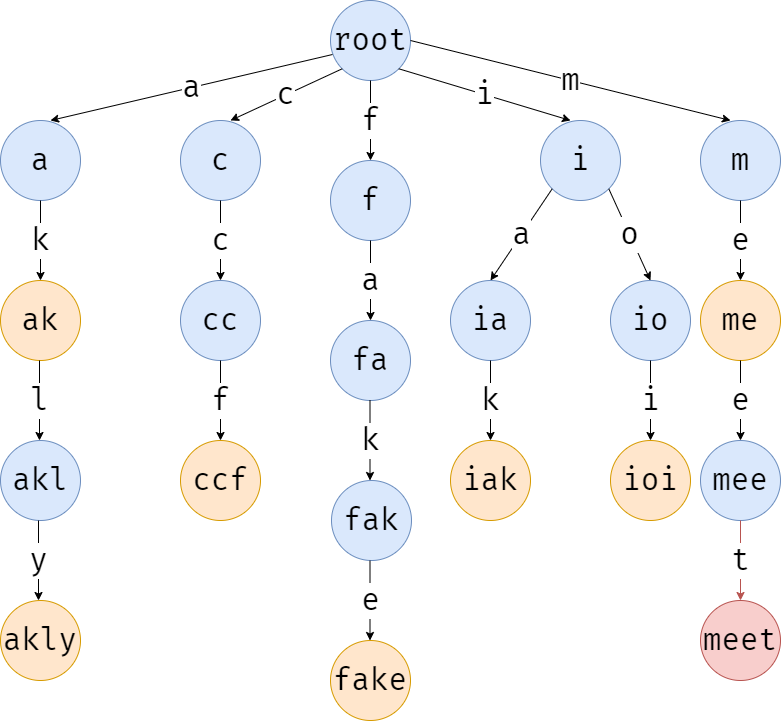
还有不要忘了标记它。
插入完成后的 Trie 长这样:
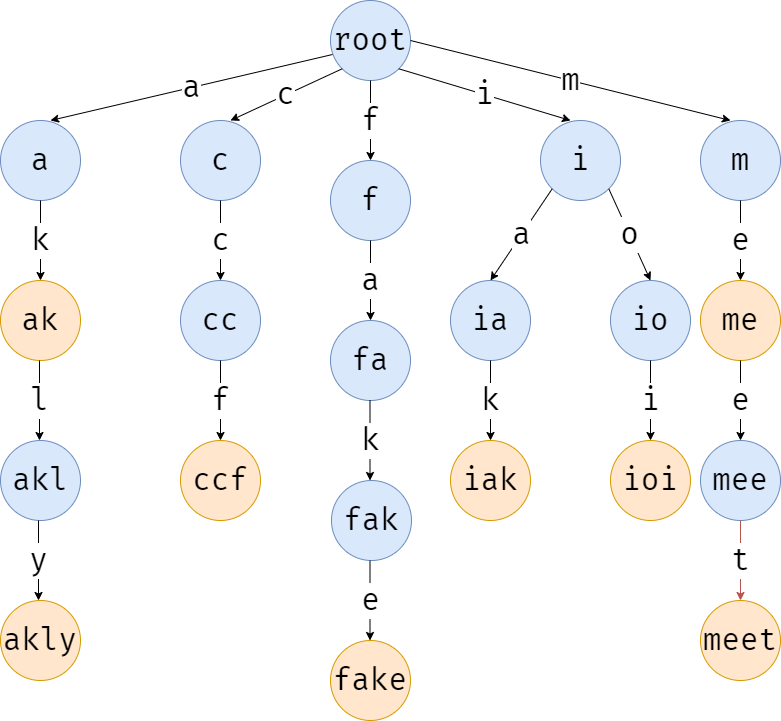
代码也很好写,就和模拟一样。
void insert(char *s){ // 传入一个字符串
u=0,l=strlen(s); // u 为当前的节点编号(初始为根节点0),l 为字符串长度
for(int i=0; i<l; i++){ // 遍历整个字符串
v=s[i]-'a'; // 获取第 i 个字符的权值
// son[u][v] 表示第 u 个节点,权值为 v 的边,指向的节点的编号
// 若 u 节点的权值为当前字符的边指向的儿子为空,说明没有这个儿子,创建
if(!son[u][v]) son[u][v]=++top;
u=son[u][v]; // 然后进入子节点
}
qt[u]++; // 标记,这里直接记录了相同字符串的个数
}
查询
查询也和插入一样,遍历一遍字符串,若遍历过程中发现要去的儿子为空,那么肯定没有要查询的字符串,直接返回。如果最后存在一个值为要查找的字符串的节点,直接返回 qt[u],即要查询的字符串个数。若以前没有插入过这个字符串,那么 qt[u] 就为 \(0\),不影响答案。
如果要查询 \(\texttt{io}\) 是否存在:
第一个字符为 \(\texttt{i}\),发现有这个儿子,进入。
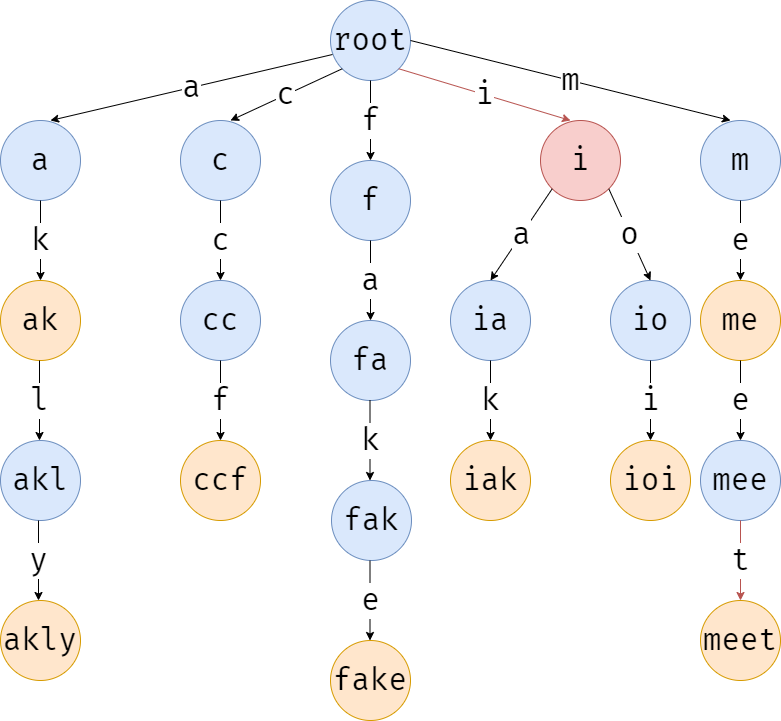
第二个字符 \(\texttt{o}\) 也有,进入。
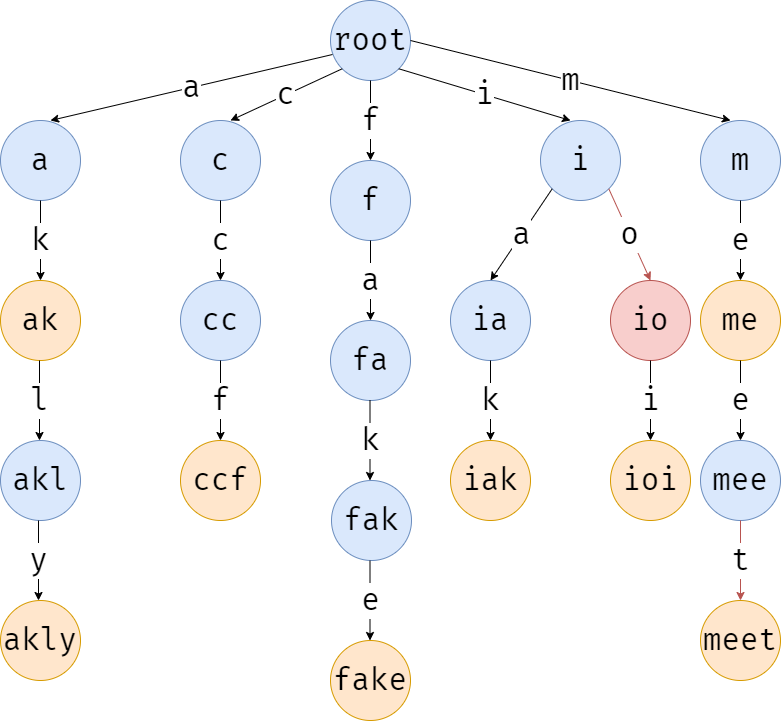
这样便找到了 \(\texttt{io}\) 节点,但是,qt 数组告诉我们,之前插入的字符串中并没有出现 \(\texttt{io}\),所以没有 \(\texttt{io}\) 这个字符串。
int find(char *s){
u=0,l=strlen(s);
for(int i=0; i<l; i++){
v=s[i]-'a';
if(!son[u][v]) return 0; // 没有对应的儿子,退出
u=son[u][v]; // 进入相应的儿子
}
return qt[u]; // 直接返回个数
}
P2580 于是他错误的点名开始了
题目大意
给定 \(n\) 个字符串,只含小写字母且长度不超过 \(50\),并给出 \(m\) 个询问,每次询问给出一个字符串,若第一次询问这个字符串,且这个字符串存在,输出 \(\texttt{OK}\)。若这个字符串存在且不是第一次询问,输出 \(\texttt{REPEAT}\)。若该字符串不存在,输出 \(\texttt{WRONG}\)。
思路
所有字符串依次插入 Trie,对于询问,若第一次询问得到,该字符串存在,那么将对应的 qt 改为 \(2\),并返回 \(1\)。否则返回 \(0\)。
那么主函数中,对于每个询问,若返回值为 \(0\),输出 \(\texttt{WRONG}\)。为 \(1\),输出 \(\texttt{OK}\),为 \(2\),就输出 \(\texttt{REPEAT}\)。
代码
#include <iostream>
#include <cstring>
using namespace std;
const int N=5e5+5,M=26;
int n,m;
char s[N];
class Trie{
public:
Trie(int (*_cvt)(char c)=[](char c)->int{return c-32;}):
top(0),cvt(_cvt){clear();}
void clear(){
for(int i=0; i<N; i++){
for(int j=0; j<M; j++)
son[i][j]=0;
qt[i]=0;
}
}
void insert(char *s,int l){
u=0;
for(int i=0; i<l; i++){
v=cvt(s[i]);
if(!son[u][v]) son[u][v]=++top;
u=son[u][v];
}
qt[u]=1;
}
int find(char *s,int l){
int u=0;
for(int i=0; i<l; i++){
int v=cvt(s[i]);
if(!son[u][v]) return 0;
u=son[u][v];
}
if(qt[u]==1){
qt[u]=2;
return 1;
}
return qt[u];
}
private:
int n,u,v;
int son[N][M],top;
int qt[N];
int (*cvt)(char c);
}t([](char c)->int{return c-'a';});
int main(){
scanf("%d",&n);
for(int i=1; i<=n; i++){
scanf("%s",s+1);
t.insert(s+1,strlen(s+1));
}
scanf("%d",&m);
while(m--){
scanf("%s",s+1);
switch(t.find(s+1,strlen(s+1))){
case 0: puts("WRONG"); break;
case 1: puts("OK"); break;
case 2: puts("REPEAT"); break;
default: break;
}
}
return 0;
}
01Trie
有这么一类问题:给定一个数,求某些数中,与这个数的最大异或值。
那么什么情况下两个数异或值最大?
首先我们要知道,异或运算,可以理解为两个二进制数是否不一样。
也就是说,它会把两个十进制数转换为二进制,并逐位比较,若不一样,则这一位为 \(1\)。否则为 \(0\)。
那么很显然,这两个数的二进制位不一样的位越多,得到的结果就越大。
于是我们就可以用 01Trie 来维护各个数的二进制。
从根节点开始的儿子,就是数的二进制最高位了。
01Trie 的边的权值只有两种:\(0\) 和 \(1\)。
查询
先来说说查询吧。
那么,给你了一棵构造好的 01Trie 和一个数,让你求出 01Trie 中的数,与这个数的最大异或值,怎么求?
肯定要尽量让每一位都不一样啦!
高位肯定是优先要不一样的,就算后面 \(n\) 位全是 \(1\),也没有第 \(n+1\) 位是 \(1\) 要大。
那么我们从高位开始贪心,看看有没有权值与当前位不一样的边。如果有,那么就进这条边指向的子节点搜。否则,就只能搜另一条了。
比如,有这么一棵 01Trie:
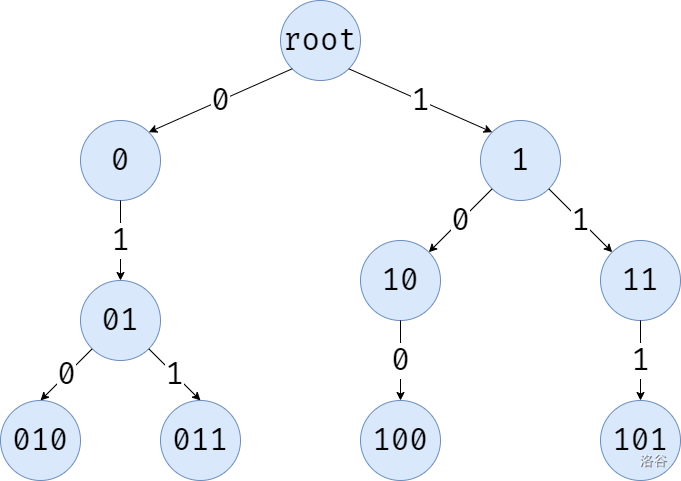
我们要插入一个二进制数 \(\texttt{111}\)。
首先,这个数的第一位为 \(1\),取反,得到 \(0\),发现有权值为 \(0\) 的出边,进入。
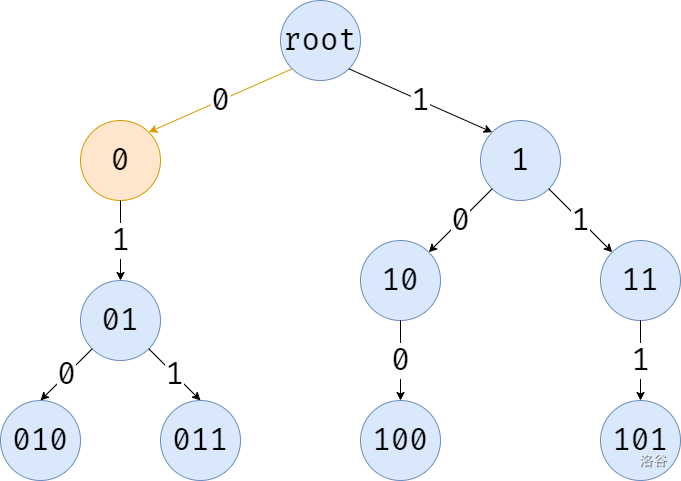
第二位也是 \(1\),但是发现没有权值为 \(0\) 的出边,那就只好走 \(1\) 了。
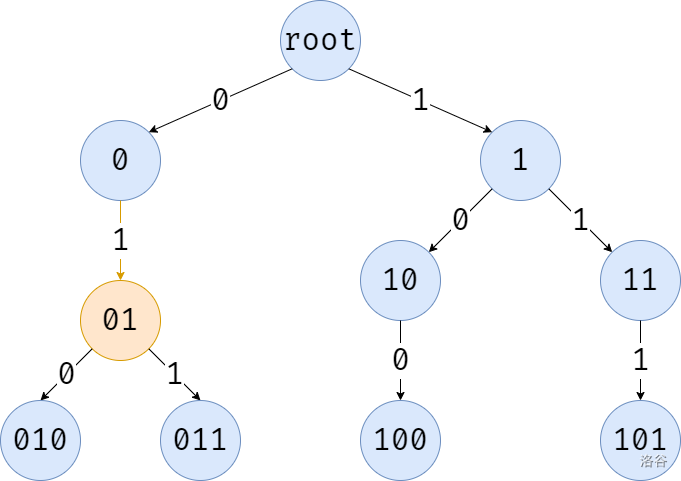
第三位还是 \(1\),有权值为 \(0\) 的出边,直接走,并结束搜索。
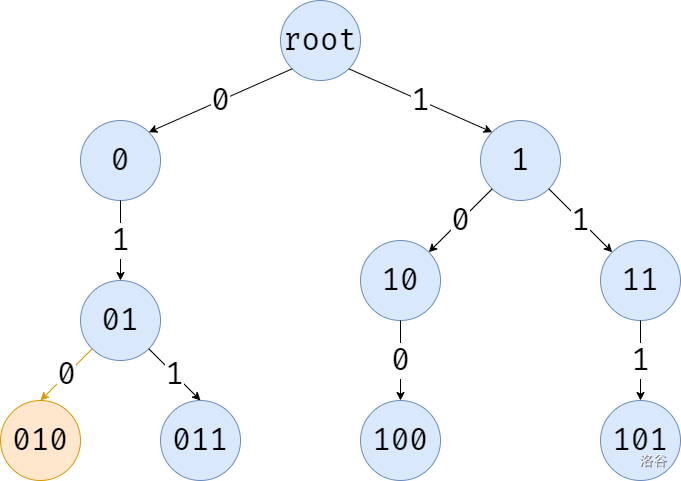
在搜索过程中,如果能走反边,那么就需要记录答案。
能走反边,意味着这一位肯定为 \(1\),答案加上对应的 \(2^i\) 即可。
ll find(ll x){
u=0,ans=0;
// 循环初始值由值域决定的,为 log_2(值域)
for(int i=32; i>=0; i--){
v=(x>>i)&1; // x 右移 i 位再 &1,就可以得到
if(son[u][!v]) u=son[u][!v],ans+=1<<i; // 可以走反边
else u=son[u][v];
}
return ans;
}
插入
也就和普通 Trie 的差不多,就不多说了。
void insert(ll x){
u=0;
// 这个循环初始值必须与查询的相同,这个值等于这棵 01Trie 的高度
for(int i=32; i>=0; i--){
v=(x>>i)&1;
if(!son[u][v]) son[u][v]=++top;
u=son[u][v];
}
}
U109895 [HDU4825]Xor Sum
题目大意
给定一个包含 \(n\) 个正整数的集合 \(a\),然后给出 \(m\) 个询问。
对于每个询问,给出一个数 \(s\),求一个正整数 \(k \in a\),使得 \(s \oplus k\) 最大。
思路
对 \(a\) 建一棵 01Trie,但查询不是求异或和了,而是求另一个参与异或的数。
统计答案的思路和上面差不多,每向下搜一层,就将当前层的数代表的值求出来,加入答案即可。
代码
#include <iostream>
#include <cstring>
using namespace std;
template<typename T=long long>
inline T read(){
T X=0; bool flag=1; char ch=getchar();
while(ch<'0' || ch>'9'){if(ch=='-') flag=0; ch=getchar();}
while(ch>='0' && ch<='9') X=(X<<1)+(X<<3)+ch-'0',ch=getchar();
if(flag) return X;
return ~(X-1);
}
template<typename T=int>
inline void write(T X){
if(X<0) putchar('-'),X=~(X-1);
T s[20],top=0;
while(X) s[++top]=X%10,X/=10;
if(!top) s[++top]=0;
while(top) putchar(s[top--]+'0');
putchar('\n');
}
typedef long long ll;
const int N=1e8+5;
ll n,m,x;
class Trie01{
public:
Trie01():top(0){clear();}
void clear(){
for(int i=0; i<n; i++)
son[i][0]=son[i][1]=0;
}
void insert(ll x){
u=0;
for(int i=32; i>=0; i--){
v=(x>>i)&1;
if(!son[u][v]) son[u][v]=++top;
u=son[u][v];
}
}
ll find(ll x){
u=0,ans=0;
for(int i=32; i>=0; i--){
v=(x>>i)&1;
if(son[u][!v]) u=son[u][v=!v]; // 这里要写 v=!v,如果要去反边,那么要加上答案的数也有变动
else u=son[u][v];
ans+=v<<i;
}
return ans;
}
private:
int son[N][2];
ll top,u,v,ans;
}t;
int main(){
n=read(),m=read();
while(n--)
t.insert(read());
while(m--)
write(t.find(read()));
return 0;
}
推荐习题
- UVA11362 Phone List
- P2922 [USACO08DEC]Secret Message G
- P2292 [HNOI2004] L 语言 这题可以用 Trie 做,但会 TLE 两个点,90pts。
- P4551 最长异或路径


