『题解』UVa online judge UVA11714 Blind Sorting

题目传送门

题目大意

给定 \(n\) 个不变但未知的正整数，每次询问可以选取两个数并得知两个数的大小关系。

问：最坏情况下，至少需要几次询问，才能知道最大数和次大数是哪两个数？

思路

我们分为两个问题：

• 最坏情况下，至少需要几次询问，才能知道最大数是哪个数？
• 最坏情况下，至少需要几次询问，才能知道次大数是哪个数？

首先看最大数，我们把这些数两两比较，找出较小数删除，再进行两两比较，例如一个长度为 \(4\) 的序列：\(1,2,3,4\)，对其进行查找最大数：

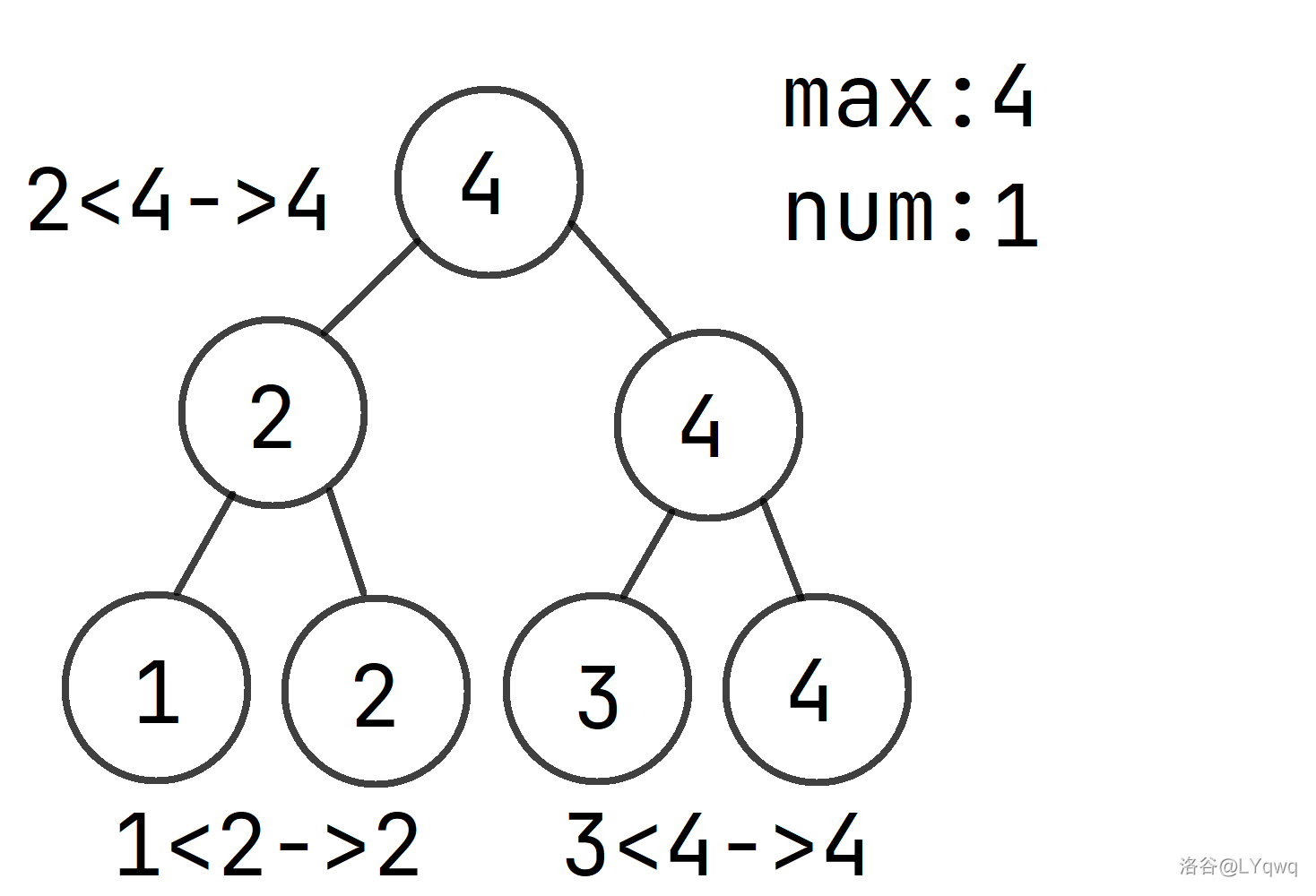
（图丑勿喷）

可以发现，从一个序列中找出最大数，只需要 \(\lfloor \log_2n-1 \rfloor\) 次比较。

而次大数，要在除去最大数里找，没有什么快点的方法，所以比较 \(n-1\) 次。

最后的答案也显而易见：\(\lfloor \log_2n-1 \rfloor +n-1\)。

代码

#include <iostream>
#include <cmath>
using namespace std;

int main(){
    int n;
    while(cin >> n){
        cout << (int)log2(n-1)+n-1 << endl;
    }
    return 0;
}