『题解』Luogu P8578 [CoE R5] So What Do We Do Now
题目大意
给定一棵 \(n\) 个结点的有根树,根结点编号为 \(1\)。设以 \(i\) 为根的子树为 \(T_i\)。你需要给每个结点赋一个正整数点权 \(v_i\),使得所有点的点权恰为 \(1,2,\dots,n\) 各一个。
记
\[f=\sum_{i=1}^{n}R_i
\]
其中 \(R_i\) 是以 \(i\) 为根的子树中点权的极差,即
\[R_i=\max_{j \in T_i}\{v_j\}-\min_{j \in T_i}\{v_j\}
\]
对于所有的赋点权的方式,请求出一组使 \(f\) 取到最小值的点权。
\(1 \le n \le 10^6\)。
思路
显然是某种思维题,我们就拿图来尝试找规律吧。
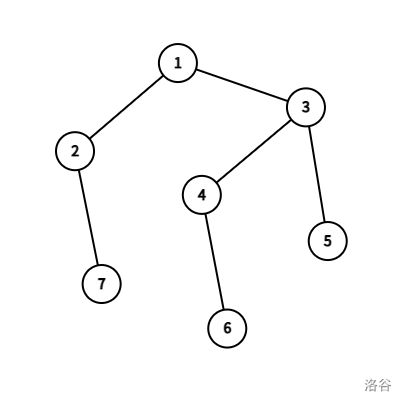
下面假设考虑的子树都是独立的,看一下每个节点的最优解会是什么。
先考虑一下节点 \(1\) 的最优解。由于它是根节点,所以子树中一定包含 \(1,\dots,7\),\(7-1=6\)。
然后看 \(2\) 号。它与子树中的节点,差值最小为 \(1\)。
\(3\) 号节点为根的子树内有 \(4\) 个节点,显然,差值最小为 \(3\)。
\(R_4\) 最小为 \(1\)。
叶子节点(\(5,6,7\))就不用说了,它们的 \(R\) 显然均为 \(0\)。
我们可以发现一个规律:\(R_i\) 在 \(i\) 为根的子树独立的情况下,可以赋一段连续的权值,这样就能保证 \(R_i\) 的最小值为子树节点个数 \(-1\)。
还有一个性质:当一棵子树的权值范围(连续的)确定后,根节点是什么都无所谓。这样我们完全可以使这棵子树的子树也有一段连续的权值可以分配,分成啥样都对这棵子树没什么区别。
于是对于上面的例子,我们可以这样分配点权:
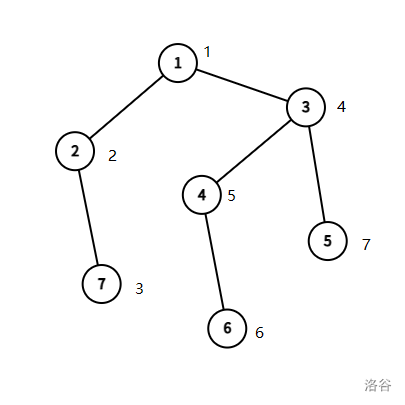
稍微观察一下,就能得出一个结论:点权就是深度优先搜索序嘛!
所以对这棵树进行一次深度优先搜索,搜到第几个权值就标几,直接输出就是答案了。
代码
#include <iostream>
using namespace std;
template<typename T=int>
inline T read(){
T X=0; bool flag=1; char ch=getchar();
while(ch<'0' || ch>'9'){if(ch=='-') flag=0; ch=getchar();}
while(ch>='0' && ch<='9') X=(X<<1)+(X<<3)+ch-'0',ch=getchar();
if(flag) return X;
return ~(X-1);
}
template<typename T=int>
inline void write(T X){
if(X<0) putchar('-'),X=~(X-1);
T s[20],top=0;
while(X) s[++top]=X%10,X/=10;
if(!top) s[++top]=0;
while(top) putchar(s[top--]+'0');
putchar('\n');
}
const int N=1e6+5,inf=0x3f3f3f3f;
struct edge{
int to,nxt;
}e[N<<1];
int n,m,u,v;
int ans[N],cnt;
int head[N],top;
void add(int u,int v){
top++;
e[top].to=v;
e[top].nxt=head[u];
head[u]=top;
}
void dfs(int u,int fa){
ans[u]=++cnt; // 标记点权
for(int i=head[u]; i; i=e[i].nxt){
int v=e[i].to;
if(v==fa) continue; // 防止子节点向父节点搜索
dfs(v,u); // 搜索
}
}
int main(){
n=read();
for(int i=1; i<n; i++){
u=read(),v=read();
add(u,v);
add(v,u);
}
dfs(1,1145141919);
for(int i=1; i<=n; i++) printf("%d ",ans[i]);
puts("");
return 0;
}


