『题解』CodeForces CF896A Nephren gives a riddle

题目传送门

题目大意

有一个字符串数组，定义如下：

• \(n=0\)：What are you doing at the end of the world? Are you busy? Will you save us?；
• \(n \neq 0\)：What are you doing while sending " \(+f_{n-1}+\) "? Are you busy? Will you send " \(+f_{n-1}+\) "?

给出 \(q\) 次询问，每次询问给出两个整数 \(n,k\)，输出 \(f_n\) 的第 \(k\) 个字符。如果 \(f_n\) 的第 \(k\) 个字符不存在，则输出 .。

数据范围：\(1 \leq q \leq 10,0 \leq n \leq 10^5,1 \leq k \leq 10^{18}\)

思路

数据范围好大...

如果试图按题意模拟，那么是存不下字符串的。

于是我们要分情况来看。

先来从 \(f_n\) 入手，它是这样的：

What are you doing while sending " +\(f_{n-1}\)+ "? Are you busy? Will you send " +\(f_{n-1}\)+ "?

我们把它分成多部分：

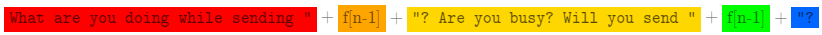
我们写一个 dfs 函数，每次寻找 \(f_n\) 的第 \(k\) 个字符。函数内分别对各种情况做了处理，包括 \(n=0\)。首先要初始化一个长度数组，能够通过 \(f_0\) 的长度推出来，然后每次 dfs 时都有很大用处。

具体见代码，注释应该够详细了吧？

记得开 long long！

代码

#include <iostream>
using namespace std;
typedef long long ll;
int q,n;
ll k;
// f就是f0，照搬；fn表示后面用来递归的原串，不包含递归串。
string f=" What are you doing at the end of the world? Are you busy? Will you save us?";
string fn=" What are you doing while sending \"\"? Are you busy? Will you send \"\"?";
// len[i]表示f[i]项的长度，先初始化好长度再进行操作。
ll len[100005]; // 注意开long long

inline ll read(){
    ll X=0; bool flag=1; char ch=getchar();
    while(ch<'0' || ch>'9'){if(ch=='-') flag=0; ch=getchar();}
    while(ch>='0' && ch<='9') X=(X<<1)+(X<<3)+ch-'0',ch=getchar();
    if(flag) return X;
    return ~(X-1);
}

void init(){ // 初始化长度
    len[0]=75; // 第一项的长度通过计算是75
    for(int i=1; i<=100000; i++){
        len[i]=len[i-1]*2+68; // 包含两个前一项的长度，68是其他的字符总长度
        if(len[i-1]<0 || len[i]>1e18){
            len[i]=-1;
        }
    }
}

void dfs(int n,ll k){
    if(n==0){ // f[0]的情况
        putchar(f[k]);
        // 直接输出，就完事了
        return;
    }
    if(k<35){ // 在第一个区间，也就是红色区间
        putchar(fn[k]);
        // 可直接输出
        return;
    }
    /*
    橙色区间情况，如果在红色区间外而且橙色区间长度，也就是f[n-1]的长度，比1e18大那就是橙色区间
    还有一种情况，也就是刚好在橙色区间中，k比34大，且小于上一个长度加上35(因为有引号)，也是橙色区间
    */
    if(len[n-1]==-1 || k>34 && k<len[n-1]+35){
        dfs(n-1,k-34);
        // 很好理解，不是红色区间的情况，k要减去前面的字符个数，再递归。
        // 绿色区间情况也一样
        return;
    }
    // 黄色区间情况
    // 在橙色区间后面且在绿色区间前面
    if(k>len[n-1]+34 && k<len[n-1]+67){
        putchar(fn[k-len[n-1]]);
        return;
    }
    // 绿色区间
    if(k>len[n-1]+66 && k<len[n-1]*2+67){
        dfs(n-1,k-len[n-1]-66);
        return;
    }
    // 否则就是蓝色区间
    putchar(fn[k-len[n-1]*2]);
}

int main(){
    init();
    q=read();
    while(q--){
        n=read(),k=read();
        if(k>len[n] && len[n]!=-1){ // k超出长度，输出'.'
            putchar('.');
            continue;
        }
        dfs(n,k); // 否则就去找！
    }
    return 0;
}