『题解』CodeForces CF1612A Distance

题目传送门

题目大意

定义两个点 \(p_1\) (坐标为 \((x_1,y_1)\)) 和 \(p_2\) (坐标为 \((x_2,y_2)\)) 之间的距离为 \(d(p_1,p_2)=|x_1-x_2|+|y_1-y_2|\)。

给定两个点 \(A(0,0),B(x,y)\) 的坐标，求一个点 \(C\) 的坐标，满足 \(d(A,C)=d(B,C)=\dfrac{d(A,B)}{2}\) (不考虑取整)。若没有合法的 \(C\) 输出 \((-1,-1)\)。

思路

题目定义的距离就是曼哈顿距离，也就是两点间的距离。

由条件 \(d(A,C)=d(B,C)=\dfrac{d(A,B)}{2}\) 可得知，\(C\) 点一定在 \(A\) 点和 \(B\) 点正中间，因为 \(A \rightarrow C=B \rightarrow C\)。可以得到：\(d(A,B)=d(A,C) \times 2=d(B,C) \times 2\)。

观察下面这张图：

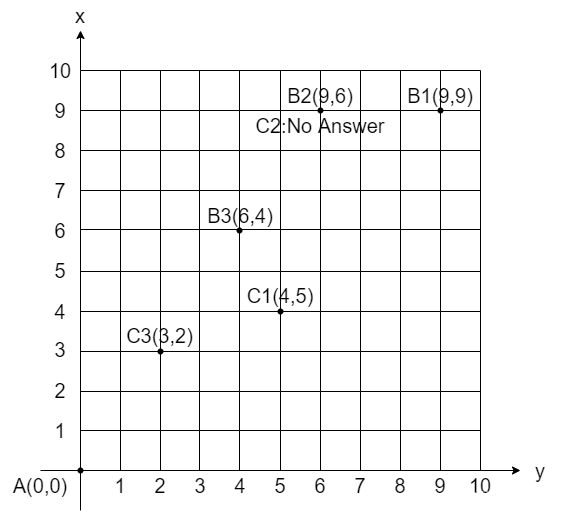
分情况讨论：

• 如果两条边奇偶性不同：通过题目中的不考虑取整可以想到，这种情况无解。

• 如果两条边都是偶数：容易想到，答案就是 \((\dfrac{x}{2},\dfrac{y}{2})\)。

• 若两条边都是奇数：还是不考虑取整，我们就取最近的一个点，答案为 \((\dfrac{x}{2},\dfrac{y}{2}+1)\)。

可以发现，图中的几个例子和样例都满足这些答案。

算出这几种情况的答案后，就没什么可说的了。

代码

(好像我代码里一个 = 都没有/jk)

#include <iostream>
using namespace std;
int n,a,b;

int main(){
    cin >> n;
    while(n--){
        cin >> a >> b;
        if((a+b)&1){
            puts("-1 -1");
        }else if(!(a%2) && !(b%2)){
            cout << a/2 << " " << b/2 << endl;
        }else{
            cout << a/2 << " " << b/2+1 << endl;
        }
    }
    return 0;
}