『学习笔记』树状数组

\(\textsf{update on 2022/6/11 修改了部分语病，代码。}\)

\(\textsf{update on 2022/10/18 优化了一下语言。}\)

\(\textsf{update on 2023/10/17 改掉一些错误（一年后又来力）。}\)

\(\textsf{update on 2023/10/17 加几道题（又一年了啊）。}\)

---

什么是树状数组

顾名思义，即数组模拟的树形结构。来看看通过一个长度为 \(8\) 的数组 \(a\) 建造出的树状数组 \(c\)。

\[\def\arraystretch{1.5} \begin{array} {|c|c|c|c|c|c|c|c|c|} \hline i&1&2&3&4&5&6&7&8\\ \hline c_i&a_1&\sum\limits^2_{i=1}a_i&a_3&\sum\limits^4_{i=1}a_i&a_5&\sum\limits^6_{i=5}a_i&a_7&\sum\limits^8_{i=1}a_i\\ \hline \end{array} \]

树状数组图如下（图中除 lowbit 外均为下标）：

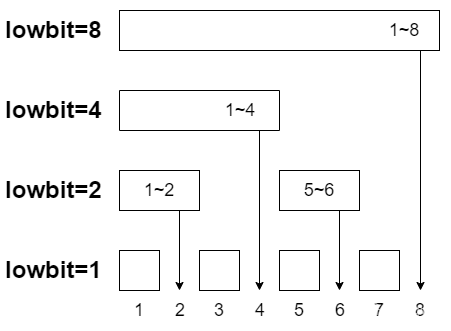
图中，有一个东西名叫 lowbit，这是树状数组的一个基本运算。

lowbit

我们可以从上面的表格中发现规律：\(c_i=a_{i-2^k+1}+a_{i-2^k+2}+\dots+a_i\) 其中 \(k\) 为 \(i\) 的二进制中末尾连续 \(0\) 的长度。

可见，\(2^k\) 决定了 \(c_i\) 包含多少 \(a\) 数组中的项，lowbit 正是求 \(2^k\) 次方的运算。我们来玩一下 \(6\) 这个数：

\(6\) 的二进制为 0110。\(k=1,2^k=2\)，可见 \(2^k\) 就是二进制的 10，可以发现，这正是 \(6\) 的二进制末尾的 \(0\) 到第一个 \(1\) 截断的数。

于是，有人想出了一种神仙计算方法：lowbit(x)=x&(-x)。其中 & 是按位与运算。

为什么呢？计算机中，存储整数有多种方式，最常用的就是补码。在 C++ 中，也是用补码存储。

那么补码又是怎样存的？

• 最高位为符号位，如果为 \(1\)，则代表负数。反之，代表正数。
• 当这个数为负数时，符号位为 \(1\)，如果要将这个数取反，后面的数，除了倒数第一个 \(1\) 及后面的所有 \(0\)，其它位全部取反。

\(6\) 的二进制补码为 0110，其中第一位符号为 \(0\)，表示正数。\(-6\) 的二进制为 \(1010\)，可见除了最后面的 10 之外，全部取反了。

而 lowbit，正是用了这个性质。负数只有倒数第一个 \(1\) 以及后面的 \(0\) 与正数相同，与正数进行按位与操作，正好是要求的数。

lowbit(x) 就是 \(c_x\) 包含的元素个数。

最基础的操作：单点修改，区间查询

这是树状数组很重要的基础操作，后面几乎所有应用都是基于或改动于这个基本操作的。

修改

例如要修改下标为 \(3\) 的元素：

要修改一个元素，需要将其上方的所有大块都修改了，才能完成修改操作。

如何找到上方的大块呢？我们可以发现一个规律：\(\texttt{包含 i 的唯一元素的下标}=i+\operatorname{lowbit}(i)\)。

那么，我们就可以从要修改的 \(3\) 开始，设为 \(i\)，每次加上 lowbit(i)，并对 \(c_i\) 进行修改。终止条件为 \(i \leq n\)。这样就能实现图中的修改操作。

代码：

void add(int i,int v){ // 将下标为 i 的元素加上 v
    while(i<=n){
        c[i]+=v;
        i+=lowbit(i);
    }
}

代码十分简单，整出这么一个结论就比较难了。

查询

先来看看如何求出 \([1,i]\) 的和。如果 \(i\) 为 \(2^n\)（即为 lowbit 的可能的结果），那么只需一次即可求得区间和，即取 \(c_i\)。那么其它情况，可以从 \(c_i\) 开始往回累加，但是区间不能重合。

我们从一个例子入手，查询区间 \([1,7]\) 的和：

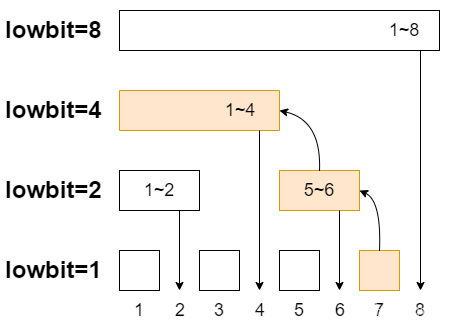
刚好是一级一级往上跳，跳到 \(1\) 了就停下。通过观察，我们发现每次只需让 \(i\) 减去 lowbit(i) 就是下一个区间块。

代码：

int sum(int i){ // 获取区间 [1,i] 的和
    int res=0;
    while(i>0){
        res+=c[i];
        i-=lowbit(i);
    }
    return res;
}

那么如果求区间 \([l,r](l \ne 1)\) 时怎么办呢？依据前缀和的思想，只需求出 sum(r)-sum(l-1) 即可。

P3374 【模板】树状数组 1

题目大意

给出一个序列，支持下面两种操作：

• 将某个数加上 \(x\)。
• 求出某区间每个数的和。

思路

树状数组的板子，直接把代码搬上来就行了。这里使用 class 封装了树状数组。

还有一个问题：如何建立树状数组。

我们刚开始时将树状数组初始化为 \(0\)，题目会给出整个序列，我们只需将各个节点加上这个节点的初始值即可。

代码

#include <iostream>
#include <cstring>
using namespace std;
template<typename T=int>
inline T read(){
    T X=0; bool flag=1; char ch=getchar();
    while(ch<'0' || ch>'9'){if(ch=='-') flag=0; ch=getchar();}
    while(ch>='0' && ch<='9') X=(X<<1)+(X<<3)+ch-'0',ch=getchar();
    if(flag) return X;
    return ~(X-1);
}

template<typename T=int>
inline void write(T X){
    if(X<0) putchar('-'),X=~(X-1);
    T s[20],top=0;
    while(X) s[++top]=X%10,X/=10;
    if(!top) s[++top]=0;
    while(top) putchar(s[top--]+'0');
    putchar('\n');
}
const int N=5e6+5; // 数据范围
int n,m,op,x,y;

template<class T=long long>
class BIT{ // 树状数组封装类
    public:
        BIT(){}
        BIT(int _n):n(_n){memset(c,0,sizeof(c));}
        void add(int x,T v){
            while(x<=n){
                c[x]+=v; // 修改
                x+=lowbit(x); // 到下一个要修改的节点
            }
        }
        T sum(int x){
            T res=0; // 总和
            while(x){
                res+=c[x]; // 累加
                x-=lowbit(x); // 到下一个要累加的节点
            }
            return res;
        }
    private:
        T c[N],n; // c是树状数组，n是节点个数
        inline T lowbit(T x){return x&-x;} // lowbit操作
};

int main(){
    // n个节点，m个操作
    n=read(),m=read();
    BIT bit(n); // 初始化树状数组
    for(int i=1; i<=n; i++) bit.add(i,read()); // 建立树状数组，直接加上去就行了
    while(m--){
        op=read();
        if(op==1){ // 修改
            x=read(),y=read();
            bit.add(x,y);
        }else{ // 求和
            x=read(),y=read();
            write(bit.sum(y)-bit.sum(x-1));
        }
    }
    return 0;
}

时间复杂度分析

• 构造：
  • 暴力：一次长度为 \(n\) 的循环，时间复杂度 \(\mathcal{O}(n)\)。
  • 树状数组：一共 \(n\) 次修改操作，每次时间复杂度 \(\mathcal{O}(\log n)\)，故时间复杂度为 \(\mathcal{O}(n \log n)\)。
• 修改：
  • 暴力：直接修改即可，时间复杂度 \(\mathcal{O}(1)\)。
  • 树状数组：从最底层开始一直向上爬，最多爬 \(\log n\) 次，所以修改时间复杂度为 \(\mathcal{O}(\log n)\)。
• 查询：
  • 暴力：从 \(l\) 扫到 \(r\)，时间复杂度 \(\mathcal{O}(n)\)。
  • 树状数组：和修改操作一样，从下往上，高度最大为 \(\log n\)，时间复杂度为 \(\mathcal{O}(\log n)\)。
• 总复杂度：
  • 暴力：\(\mathcal{O}(nm)\)。
  • 树状数组：\(\mathcal{O}((n+m) \log n)\)。

对树状数组进行差分

这里就需要使用到差分思想了。在树状数组中的实现是与上面一样的，只不过调用函数的方式不一样。差分可以让树状数组支持更复杂的操作，下面就是几个例子。这些操作用线段树写起来比较麻烦，但是树状数组却相反。

（不懂差分的可以参考这篇文章，暂时只需要用到一维差分。）

区间修改，单点查询

我们不需要动上面写好的树状数组类，只是在调用其函数时有些变动，就可以实现区间修改，单点查询的操作。

我们先考虑只用一个差分数组，直接维护序列。核心代码如下：

n=read(),m=read(); // n 为序列长度，m 为操作个数
for(int i=1; i<=n; i++){
    a[i]=read();
    dif[i]=a[i]-a[i-1]; // 构造差分数组
}
while(m--){
    op=read();
    if(op==1){
        x=read(),y=read(),k=read();
        dif[x]+=k;
        dif[y+1]-=k;
    }else{
        x=read();
        for(int i=1; i<=n; i++)
            a[i]=a[i-1]+dif[i]; // 求前缀和
        write(a[x]);
    }
}

复杂度有点危，我们可以通过树状数组来优化。我们使用树状数组代替 \(dif\) 数组，代码中对 \(dif\) 数组的几个操作树状数组都能很好地支持，还比原来的要快。

构造

和上面 单点修改，区间查询 的操作一样，只不过要赋的值为 \(a_i-a_{i-1}\)。而后面不需要用数组 \(a\) 了，所以我们使用滚动数组。

for(int i=1; i<=n; i++){
    b=read(); // 滚动数组
    bit.add(b-a); // add 进树状数组
    a=b;
}

树状数组 bit 也和上面的一模一样，只是操作的数不一样，就能完成 区间修改，单点查询 的操作。

修改

同上，将第 \(x\) 个数加上 \(k\)，将第 \(y+1\) 个数减去 \(k\)，也就是加上 \(-k\)，就可以实现区间修改。

bit.add(x,k);
bit.add(y+1,-k);

查询

要求第 \(x\) 个数是多少，对树状数组进行一次前缀和操作，操作到第 \(x\) 个数就可以了，并不需要全部都进行前缀和操作。树状数组中的 sum 操作刚好是这样的。

write(bit.sum(x));

P3368 【模板】树状数组 2

题目大意

给定一个长度为 \(N\) 的序列和 \(M\) 个操作，操作有一下两种：

1. 1 x y k：将区间 \([x,y]\) 内的每个数加上 \(k\)。
2. 2 x：求第 \(x\) 个数的值。

代码

#include <iostream>
#include <cstring>
using namespace std;
template<typename T=int>
inline T read(){
    T X=0; bool flag=1; char ch=getchar();
    while(ch<'0' || ch>'9'){if(ch=='-') flag=0; ch=getchar();}
    while(ch>='0' && ch<='9') X=(X<<1)+(X<<3)+ch-'0',ch=getchar();
    if(flag) return X;
    return ~(X-1);
}

template<typename T=int>
inline void write(T X){
    if(X<0) putchar('-'),X=~(X-1);
    T s[20],top=0;
    while(X) s[++top]=X%10,X/=10;
    if(!top) s[++top]=0;
    while(top) putchar(s[top--]+'0');
    putchar('\n');
}

const int N=5e5+5; // 数据范围
int n,m,a,b,op,x,y,k;

template<class T=int>
class BIT{ // 树状数组封装类
    public:
        BIT(){}
        BIT(int _n):n(_n){memset(c,0,sizeof(c));}
        void add(int x,T v){
            while(x<=n){
                c[x]+=v; // 修改
                x+=lowbit(x); // 到下一个要修改的节点
            }
        }
        T sum(int x){
            T res=0; // 总和
            while(x){
                res+=c[x]; // 累加
                x-=lowbit(x); // 到下一个要累加的节点
            }
            return res;
        }
    private:
        T c[N],n; // c 是树状数组，n 是节点个数
        inline T lowbit(T x){return x&-x;} // lowbit 操作
};

int main(){
    // n 个节点，m 个操作
    n=read(),m=read();
    BIT<long long> bit(n); // 初始化树状数组
    for(int i=1; i<=n; i++){
        b=read();
        bit.add(i,b-a); // 建立树状数组
        // 由于是区间修改，要将第 i 项加上 a[i] 再减去 a[i-1]
        // 要做一个差分，所以直接加上 a[i]-a[i-1]，是负数也没关系
        // 不需要记录 a 数组的值，所以使用滚动数组
        a=b;
    }
    while(m--){
        op=read();
        if(op==1){ // 修改
            x=read(),y=read(),k=read();
            bit.add(x,k); // 将区间 [x,n] 加上k
            bit.add(y+1,-k); // 区间 [y+1,n] 减去k
            // 由于做了差分，修改 i 等于修改了区间 [i,n]，将 [x,n] 加上了再将 [y+1,n] 减去就刚好实现了区间修改
        }else{ // 求和
            x=read();
            write(bit.sum(x));
        }
    }
    return 0;
}

时间复杂度分析

• 构造：
  • 普通差分：直接修改即可，时间复杂度 \(\mathcal{O}(1)\)。
  • 树状数组优化：执行一次 add，时间复杂度 \(\mathcal{O}(\log n)\)。
• 修改：
  • 普通差分：直接修改 dif 数组，时间复杂度 \(\mathcal{O}(\log n)\)。
  • 树状数组优化：执行两次 add，时间复杂度 \(\mathcal{O}(\log n)\)。
• 查询：
  • 普通差分：执行前缀和操作，最坏情况下 \(x=n\)，时间复杂度 \(\mathcal{O}(n)\)。
  • 树状数组优化：执行一次 sum，时间复杂度 \(\mathcal{O}(\log n)\)。
• 总复杂度：
  • 普通差分：\(\mathcal{O}(nm)\)。
  • 树状数组优化：\(\mathcal{O}(m \log n)\)。

区间修改，区间查询

可以尝试用上一种树状数组实现这个操作，问题主要在于区间查询。每次查询的是一个点，那么要求的就是 \(\sum\limits^{r}_{i=l}\operatorname{sum(i)}\)，复杂度显然超标。

我们可以尝试分别求 \(\sum\limits^{l-1}_{i=1}a_i\) 和 \(\sum\limits^{r}_{i=1}a_i\)，然后相减得到答案。

那么树状数组的 sum 函数的任务就是求出 \(\sum\limits^{x}_{i=1}a_i\) 了。

尝试化简一下最终答案的式子：

\[\begin{aligned}  \operatorname{sum}&=\sum\limits^{x}_{i=1}\sum\limits^{i}_{j=1}a_j\\  &=\sum\limits^{x}_{i=1}[(x-i+1) \times a_i]\\  &=\sum\limits^{x}_{i=1}[x \times a_i - (i-1) \times a_i]\\  &=\sum\limits^{x}_{i=1}(x \times a_i) - \sum\limits^{x}_{i=1}[(i-1) \times a_i]\\  &=x \times \sum\limits^{x}_{i=1}a_i - \sum\limits^{x}_{i=1}[(i-1) \times a_i]\\ \end{aligned} \]

我们可以发现，可以维护两个树状数组，分别存放 \(a_i\) 与 \((i-1) \times a_i\)，区间加时同时维护，区间查询时可根据最后化简得来的式子得出：\(ans=n \times a-b\)，其中 \(a\) 为第一个树状数组的 sum(x) 操作返回值，\(b\) 同上。

这样一来，实现这个看似很难操作似乎也变得很容易了，代码也挺容易理解的，只是有些区别。

修改

我们直接重写树状数组的修改与查询操作，在类中定义两个树状数组 \(ca,cb\)，分别维护 \(a_i\) 与 \((i-1) \times a_i\)。

这里同样是在维护一个差分数组。

在 add 函数中，保存原有的参数 \(x\)，定义一个变量 \(i\) 用于循环累加。每次累加， \(ca \gets v,cb \gets (x-1) \times v\)，就能完成两个树状数组的维护。

void add(int x,T v){
    for(int i=x; i<=n; i+=lowbit(i)){
        ca[i]+=v;
        cb[i]+=(x-1)*v;
    }
}

这个函数的作用和上面的区间改单点查一样，都是将 \([x \ldots n]\) 加上 \(v\)。如果要将区间 \([x \ldots y]\) 都加上 \(k\)，那么可以这么调用：

bit.add(x,k);
bit.add(y+1,-k);

查询

和修改一样，保留原有的 \(x\) 用于计算答案。我们可以通过计算上面最终的式子 \(x \times \sum\limits^{x}_{i=1}c_i - \sum\limits^{x}_{i=1}[(i-1) \times c_i]\) 来得出答案。

不需要两个循环，合并在一个循环内就可以了。每次循环令答案加上 x*ca[i]-cb[i] 即可得到 \(\sum\limits^{x}_{i=1}a_i\) 了。

T sum(int x){
    T res=0;
    for(int i=x; i; i-=lowbit(i))
        res+=x*ca[i]-cb[i];
    return res;
}

求 \(\sum\limits^{r}_{i=l}a_i\) 也很简单，只需求出 bit.sum(y)-bit.sum(x-1) 即可。

P3372 【模板】线段树 1

题目大意

给定长度为 \(n\) 的序列 \(a\) 和操作个数，每次操作可能是以下两种：

1. 1 x y k：将区间 \([x \ldots y]\) 内每个数加上 \(k\)。
2. 2 x y：求 \(\sum\limits^{y}_{i=x}a_i\)。

思路

套上面的板子，直接看代码就行。

代码

#include <iostream>
using namespace std;
template<typename T=int>
inline T read(){
    T X=0; bool flag=1; char ch=getchar();
    while(ch<'0' || ch>'9'){if(ch=='-') flag=0; ch=getchar();}
    while(ch>='0' && ch<='9') X=(X<<1)+(X<<3)+ch-'0',ch=getchar();
    if(flag) return X;
    return ~(X-1);
}

template<typename T=int>
inline void write(T X){
    if(X<0) putchar('-'),X=~(X-1);
    T s[20],top=0;
    while(X) s[++top]=X%10,X/=10;
    if(!top) s[++top]=0;
    while(top) putchar(s[top--]+'0');
    putchar('\n');
}

const int N=1e5+5;
int n,m,a,b,op,x,y,k;

template<class T=int>
class BIT{
    public:
        BIT(int _n=0):n(_n){memset(ca,0,sizeof(ca)),memset(cb,0,sizeof(cb));}
        void add(int x,T v){ // 修改，查询操作不多说了
            for(int i=x; i<=n; i+=lowbit(i)){
                ca[i]+=v;
                cb[i]+=(x-1)*v;
            }
        }
        T sum(int x){
            T res=0;
            for(int i=x; i; i-=lowbit(i))
                res+=x*ca[i]-cb[i];
            return res;
        }
    private:
        T ca[N],cb[N],n; // 两个树状数组，分别维护 c[i] 与 (i-1)*c[i]
        inline T lowbit(T x){return x&-x;}
};
BIT<long long> bit(n);

int main(){
    n=read(),m=read();
    for(int i=1; i<=n; i++){
        b=read();
        bit.add(i,b-a);
        a=b;
    }
    while(m--){
        op=read();
        if(op==1){
            x=read(),y=read(),k=read();
            bit.add(x,k);
            bit.add(y+1,-k);
        }else{
            x=read(),y=read();
            write(bit.sum(y)-bit.sum(x-1));
        }
    }
    return 0;
}

复杂度同上。

树状数组简单应用

P6225 [eJOI2019] 异或橙子

单点修改，区间查询所有子区间的异或和的异或和。

考虑每一个 \(a_i\) 对区间 \([l,r]\) 的贡献。\(a_i\) 一共会被异或入答案 \((i-l+1)(r-i+1)\) 次，由异或的消去律，只需考虑其奇偶性即可。

• 若 \(r-l+1\) 为偶数，则 \(a_i\) 贡献为 \(0\)。
• 为奇数，\(l\) 与 \(r\) 奇偶性相同。则若 \(i\) 与其奇偶性相同，贡献为 \(a_i\)；否则为 \(0\)。

由此，建立两个树状数组，分别维护奇数位与偶数位区间异或和即可。

树状数组上倍增

单点修改并立即查询序列中第 \(k\) 小的数。数据范围 \([1,10^5]\)，值域 \([1,10^5]\)。

很容易想到可以按值域建树状数组然后二分答案。但是时间复杂度 \(O(\log^2n)\)。

有点高。尝试倍增。设当前倍增到 \(r\)，需要考虑 \(r+2^d\) 是否包含 \(k\)。于是这个 \(2^d\) 在树状数组中就显得很微妙，尝试将其与 \(\text{lowbit}\) 联系？将 \([1,r+2^d]\) 拆为 \([1,r]\) 与 \([r+1,r+2^d]\)。由于 \(d\) 降序枚举，很显然 \(r+2^d\) 就是将 \(r\) 末尾第 \(d\) 个 \(0\) 变为 \(1\)，不就是加上 \(\text{lowbit}\) 吗？\([r+1,r+2^d]\) 数的个数即为树状数组中 \(c[r+2^d]\)。累加可以 \(O(1)\) 拿到 \([1,r+2^d]\) 的数的个数。于是时间复杂度降为 \(O(\log n)\)。

P6619 [省选联考 2020 A/B 卷] 冰火战士

TODO...