『学习笔记』二叉搜索树
二叉搜索树(Binary Search Tree,BST)可以 \(\mathcal{O}(\log n)\) 地完成一些修改和查询操作。如:
- 插入一个数。
- 删除一个数。
- 查询某个数的排名(排名定义为比当前数小的数的个数 \(+1\)。若有多个相同的数,取最小的排名)。
- 查询排名为某个数的数。
- 查询某个数的前驱(前驱定义为小于这个数,且最大的数)。
- 查询某个数的后继(后继定义为大于这个数,且最小的数)。
二叉搜索树的时间复杂度比较优秀,上面这些操作的复杂度均为 \(\mathcal{O}(\log n)\)。
二叉搜索树有一个核心性质:\(\text{左儿子}<\text{父亲}<\text{右儿子}\)。
所以,它的中序遍历始终保持升序。
例如,依次插入 \(6,9,4,3,2,5,7,10\),这棵树长这样:
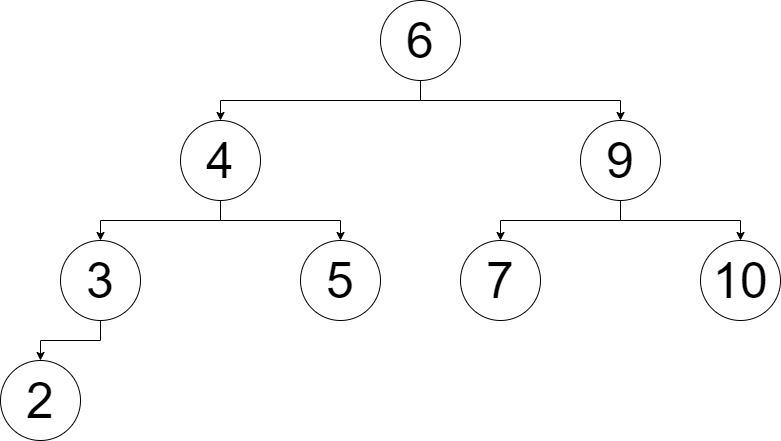
插入
要插入一个数,怎么样把它放到合适的位置?
当然是将其与根节点比较,如果小于根节点 \(6\),那么肯定要放进左儿子。否则,就一定在右儿子中。
确定了在左儿子还是右儿子后,还要对确定的节点比较,和上面与根节点比较一样。
就一直这么比较,直到找到某个节点,满足:
- 插入的数 \(<\) 这个节点,并且左儿子为空。
- 插入的数 \(>\) 这个节点,并且右儿子为空。
- 插入的数 \(=\) 这个节点。
这三条满足任意一条,就可以停止搜索了。
若是满足前两条中的一条,那么就新建相应的儿子,并设为插入的数。
否则,满足第三条,则使这个节点的的 cnt 加一。
cnt 为各个节点的出现次数,防止将相同节点插入到 BST 中。
拿 \(8\) 来举例子吧。
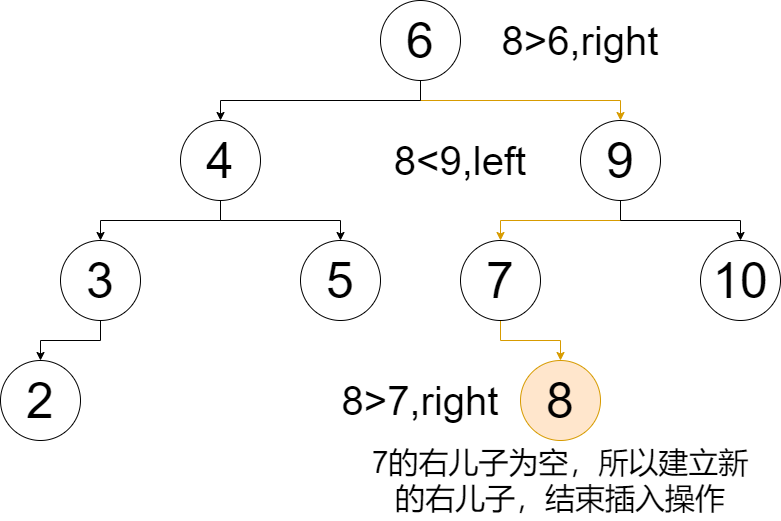
void insert(int rt,int v){
a[rt].size++; // size 用于记录某棵子树中的节点个数
if(a[rt].cnt==0 && a[rt].l==0 && a[rt].r==0){ // 当遇到一个空节点
a[rt].val=v; // 设置值,个数
a[rt].cnt=1;
}else if(v<a[rt].val){ // 进左儿子
if(a[rt].l==0) a[rt].l=++top; // 如果左儿子为空,则新建,继续递归,会进入上面那个if
insert(a[rt].l,v); // 递归左儿子
}else if(v>a[rt].val){ // 进右儿子
if(a[rt].r==0) a[rt].r=++top; // 同上
insert(a[rt].r,v);
}else a[rt].cnt++; // v==a[rt].val,让节点个数++
}
删除
删除可以直接采用惰性删除。
我们只把找到的节点的 cnt 减去一,也不管左儿子右儿子谁替换删除的这个节点的问题,那样不但复杂,还增加复杂度。
就算找到的这个节点的 cnt 为 \(0\) 了,它的值还在,可以继续从它这里找左儿子和右儿子。
如果之后又插入一个 cnt 为 \(0\) 的节点,我们可以直接让它 cnt++,子树什么的不用管。
void remove(int rt,int v){
a[rt].size--; // 子树的节点个数--
if(v<a[rt].val) remove(a[rt].l,v); // 左儿子
else if(v>a[rt].val) remove(a[rt].r,v); // 右儿子
else a[rt].cnt--; // 直接-
}
排名
我们不仅可以求某个数正着数第几名,还可以求它是倒数第几。
这里我们的 rankl(rank less)和 rankg(rank greater),都只求比某个数小或大的数的个数,如果要输出排名,需要加一。
拿 rankl 来说。
同样,递归搜:
- 若要找的值小于当前节点,那么肯定去左儿子搜。没有左儿子就直接返回 \(0\)。
- 否则,要去右儿子。但如果要去右儿子,显然左儿子和根节点的所有节点都比要找的值小,所以返回的值要加上左儿子的大小和根节点的
cnt,再去右儿子搜。若没有右儿子,则不去右儿子了,直接返回。 - 最后一种情况,要找的值与当前节点的值相等,返回左儿子大小即可。
前面的插入删除中,都有一个 size++ 和 size--,这个 size 就是在这里用上的。
int rankl(int rt,int v){
if(v<a[rt].val) // 左儿子
return a[rt].l ? rankl(a[rt].l,v) : 0;
if(v>a[rt].val) // 右儿子,返回根节点个数+左儿子大小+
return a[rt].cnt+a[a[rt].l].size+(a[rt].r ? rankl(a[rt].r,v) : 0);
return a[a[rt].l].size;
}
rankg 同理。
int rankg(int rt,int v){
if(v>a[rt].val)
return a[rt].r ? rankg(a[rt].r,v) : 0;
if(v<a[rt].val)
return a[rt].cnt+a[a[rt].r].size+(a[rt].l ? rankg(a[rt].l,v) : 0);
return a[a[rt].r].size;
}
求指定排名的数
还是老办法,递归。
设排名为 \(k\)。
如果 \(k\) 比左子树的大小要小,那么就要去左子树。
左子树的大小加上根节点节点个数,如果小于 \(k\) 的话,就肯定不在左子树中,要去右子树。可去了右子树,\(k\) 就不对了,需要减去左子树大小和根节点节点个数,才能得到正确的排名。
否则,就找到了答案,返回即可。
int kth(int rt,int k,int err=2147483647){ // err 为找不到排名为 k 的数时的返回值
if(a[rt].val==0 && a[rt].l==0 && a[rt].r==0)
return err; // 若进入的子树为空,返回
if(k<=a[a[rt].l].size)
return kth(a[rt].l,k);
if(k>a[rt].cnt+a[a[rt].l].size)
return kth(a[rt].r,k-a[rt].cnt-a[a[rt].l].size);
return a[rt].val;
}
前驱
可以直接通过 kth 和 rankl 来求排名比当前数小 \(1\) 的数。
int pre(int v){return kth(1,rankl(1,v));}
后继
后继的排名是小于或等于当前数的数的数量 \(+1\)。
int suc(int v){return kth(1,a[1].size-rankg(1,v)+1);}
由于 rankl 只返回比当前数小的数的个数,所以直接用树的总结点个数减去比当前数大的数的个数并加一即可。
P5076 【深基16.例7】普通二叉树(简化版)
板子。
代码
#include <iostream>
using namespace std;
template<typename T=int>
inline T read(){
T X=0; bool flag=1; char ch=getchar();
while(ch<'0' || ch>'9'){if(ch=='-') flag=0; ch=getchar();}
while(ch>='0' && ch<='9') X=(X<<1)+(X<<3)+ch-'0',ch=getchar();
if(flag) return X;
return ~(X-1);
}
template<typename T=int>
inline void write(T X){
if(X<0) putchar('-'),X=~(X-1);
T s[20],top=0;
while(X) s[++top]=X%10,X/=10;
if(!top) s[++top]=0;
while(top) putchar(s[top--]+'0');
putchar('\n');
}
int q,op,x;
template<class T=int>
class BST{
public:
BST(int n=5e5):top(1){
a=new node[n+5];
for(int i=0; i<n; i++)
a[i]={0,0,0,0,0};
}
void insert(int rt,T v){
a[rt].size++;
if(a[rt].cnt==0 && a[rt].l==0 && a[rt].r==0){
a[rt].val=v;
a[rt].cnt=1;
}else if(v<a[rt].val){
if(a[rt].l==0) a[rt].l=++top;
insert(a[rt].l,v);
}else if(v>a[rt].val){
if(a[rt].r==0) a[rt].r=++top;
insert(a[rt].r,v);
}else a[rt].cnt++;
}
void remove(int rt,T v){
a[rt].size--;
if(v<a[rt].val) remove(a[rt].l,v);
else if(v>a[rt].val) remove(a[rt].r,v);
else a[rt].cnt--;
}
int rankl(int rt,T v){
if(v<a[rt].val)
return a[rt].l ? rankl(a[rt].l,v) : 0;
if(v>a[rt].val)
return a[rt].cnt+a[a[rt].l].size+(a[rt].r ? rankl(a[rt].r,v) : 0);
return a[a[rt].l].size;
}
int rankg(int rt,T v){
if(v>a[rt].val)
return a[rt].r ? rankg(a[rt].r,v) : 0;
if(v<a[rt].val)
return a[rt].cnt+a[a[rt].r].size+(a[rt].l ? rankg(a[rt].l,v) : 0);
return a[a[rt].r].size;
}
T kth(int rt,int k,int err=2147483647){
if(a[rt].val==0 && a[rt].l==0 && a[rt].r==0)
return err;
if(k<=a[a[rt].l].size)
return kth(a[rt].l,k);
if(k>a[rt].cnt+a[a[rt].l].size)
return kth(a[rt].r,k-a[rt].cnt-a[a[rt].l].size);
return a[rt].val;
}
T pre(T v){return kth(1,rankl(1,v),-2147483647);}
T suc(T v){return kth(1,a[1].size-rankg(1,v)+1);}
private:
int top;
struct node{
T val;
int l,r;
int size,cnt;
}*a;
};
BST t;
int main(){
q=read();
while(q--){
op=read(),x=read();
switch(op){
case 1: write(t.rankl(1,x)+1); break;
case 2: write(t.kth(1,x)); break;
case 3: write(t.pre(x)); break;
case 4: write(t.suc(x)); break;
case 5: t.insert(1,x); break;
default: break;
}
}
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号