『学习笔记』二叉堆
堆(Heap)是一类数据结构,它们是一种树形结构,而且父节点比子节点小(或大)。这样,堆的根节点就一定是所有元素中最小(或最大的)。父节点比子节点小的叫做小根堆,反之,叫做大根堆。
二叉堆是最常见的堆,它结构简单,代码也挺好写,可以 \(\mathcal{O}(\log n)\) 插入或删除某个值,\(\mathcal{O}(1)\) 查询所有值中最小(或最大)的值。
例如有 \(10\) 个元素 \(1,2,4,5,3,4,7,9,6,9\),我们将它们依次插入到一个空的小根堆,那么这个小根堆是这样的:
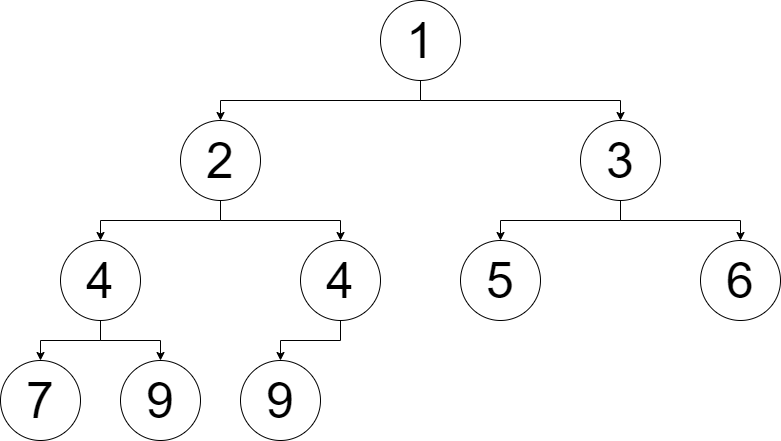
如何存储
可以发现,二叉堆是一颗完全二叉树。
于是,这棵树便可以用一个数组来存储。
对于一个下标为 \(x\) 的节点,它的左孩子的下标在 \(2x\),右孩子的下标在 \(2x+1\)。
这样,在这个数组的末尾添加元素,就等于在这棵树上的末尾,按照『从上到下,从左到右』的顺序添加元素。
看下面这棵树,节点上标的是各个元素在这个数组中的下标。
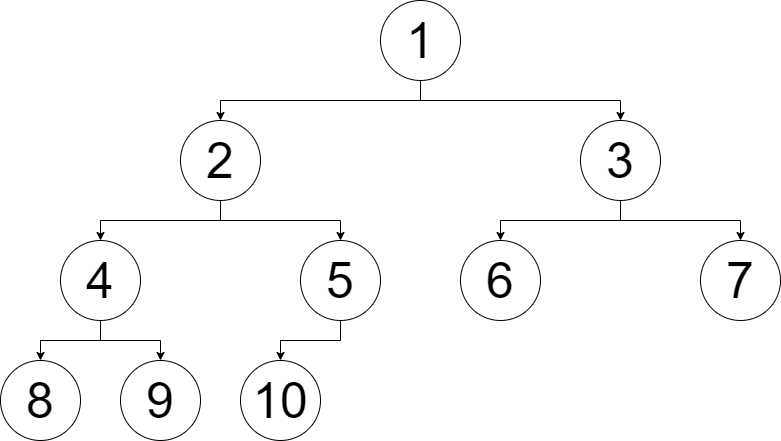
在数组中则是这样:
可见所有节点的左右孩子均为 \(2x\) 和 \(2x+1\),现在的末项为 \(10\),若再加一项,\(11\) 便为数组末项,刚好是 \(5\) 的右儿子。
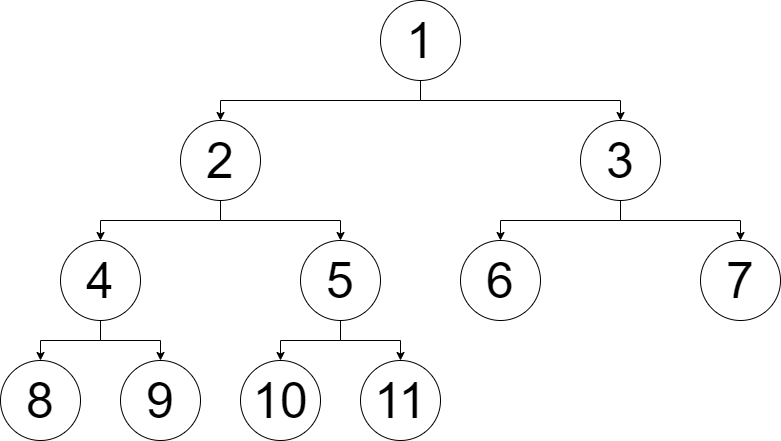
那么,如果第 \(11\) 个元素比 \(9\) 小,是 \(0\),怎么办?
为了维护堆的性质,我们需要用到两个操作:上浮和下沉。
上浮
上浮,顾名思义,就是要让某个元素,浮到自己应该到的位置。
什么时候要上浮呢?就当这个元素不满足堆的性质的时候。小根堆中,父节点必须比子节点小。
就拿上面的第 \(11\) 个元素做例子,是 \(0\),而它的父节点却是 \(4\),不满足父节点比子节点小的性质。
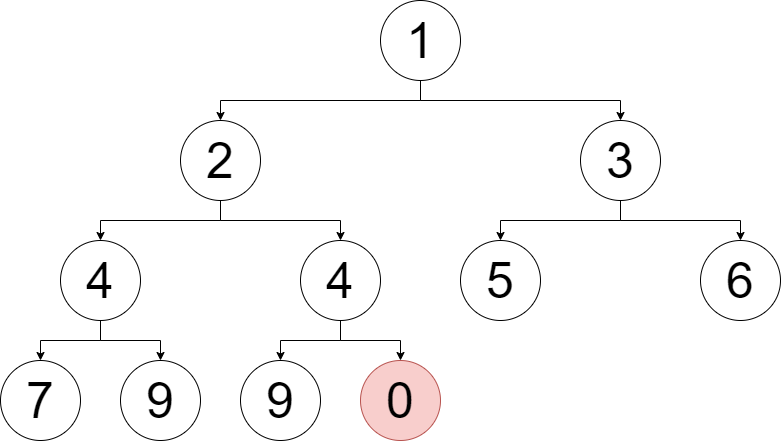
显然,可以让 \(0\) 和父节点 \(4\) 交换位置,尝试满足堆的性质。
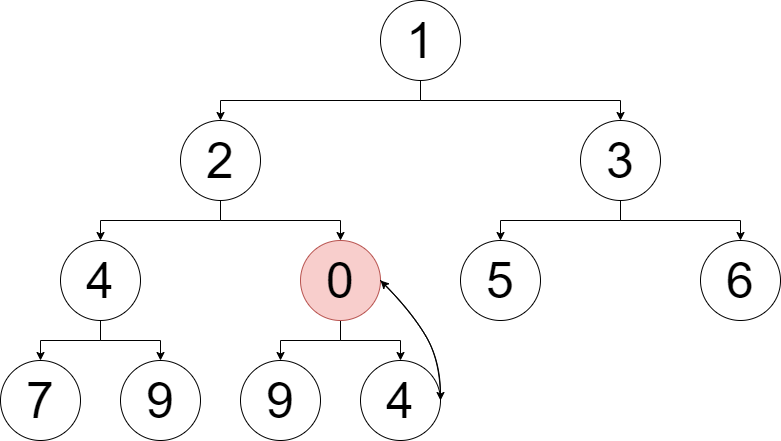
可交换后发现,\(0>2\),还是比父节点大。所以再交换一次。
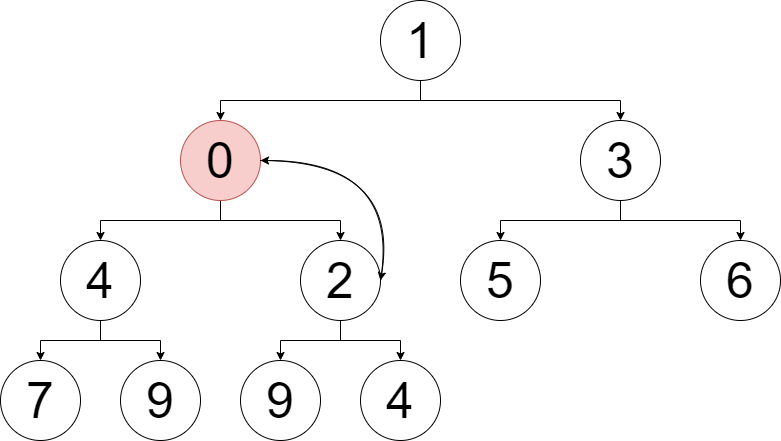
\(0\) 还是比父节点 \(1\) 大,所以再交换。
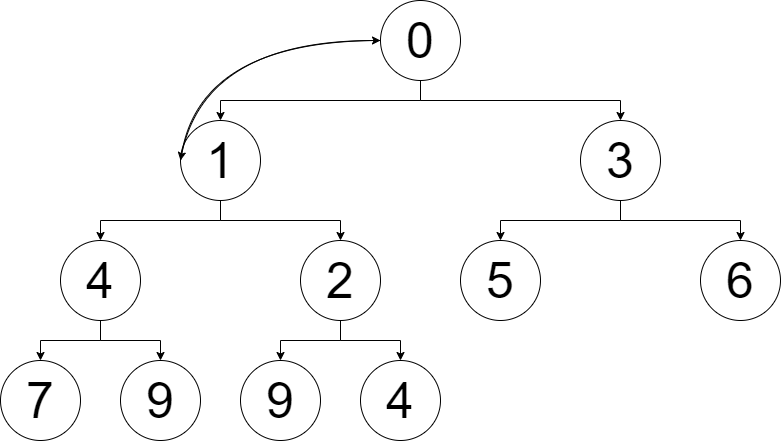
这时,\(0\) 到达了堆顶,终于使得堆满足了性质,所以对 \(0\) 的上浮操作结束。
void swim(int x){
for(int i=x; i>1 && a[i]<a[i>>1]; i>>=1)
swap(a[i],a[i>>1]);
}
上浮函数的参数 \(x\) 即为要上浮的节点在数组中的下标,上面例子中是 \(11\)。
循环中的 \(i\) 即为要上浮的节点的下标,可能到父节点(也就是 \(\dfrac{i}{2}\),可以直接使用位运算 i>>1 来计算),当这个节点已经到了堆顶或是父节点比当前节点小了,循环就退出,操作结束。
每次循环都会交换 \(i\) 节点和 \(i\) 的父节点,最坏情况是从堆的底部上浮的堆顶,所以上浮的时间复杂度为 \(\mathcal{O}(\log n)\)。
下沉
有上浮,自然就有下沉。
下沉和上浮很像,就不多说了,就是将一个节点与较小的子节点比较,如果它比这个子节点要大,就需要交换,直到这个节点的子节点不小于它。
注意要与较小的子节点比较,因为父节点可能大于较小的子节点,却小于较大的子节点,选了较大的就不会交换了。
inline int ls(int x){return x<<1;} // 计算左儿子
inline int rs(int x){return x<<1|1;} // 计算右儿子
// son 函数返回较小的子节点
inline int son(int x){return ls(x)+(rs(x)<=l && a[rs(x)]<a[ls(x)]);}
void sink(int x){
// t 即为较小的子节点,需要小于或等于堆的长度,同时也要满足它比父节点要小,才能交换
for(int i=x,t=son(i); t<=l && a[t]<a[i]; i=t,t=son(i))
swap(a[i],a[t]);
}
各种操作
构造
可以通过一个数组建立堆,先将这个数组直接复制到堆中,然后再考虑对元素上浮或下沉。
显然,一种暴力的做法就是把所有节点都上浮或下沉一遍,时间复杂度 \(\mathcal{O}(n \log n)\)。
于是就不知道从哪里诞生了一种 \(\mathcal{O}(n)\) 的做法:从下标为 \(\dfrac{n}{2}\) 的节点开始,自底向上下沉,叶子节点不需要下沉。那么对于各个需要下沉的节点,最坏情况下:
- 最下层的 \(\dfrac{n}{2}\) 个叶子节点不需要下沉。
- 次下层的 \(\dfrac{n}{4}\) 个节点需要下沉 \(1\) 层,即与较小的子节点交换。共下沉 \(1 \times \dfrac{n}{4}\) 次。
- 倒数第 \(3\) 层的 \(\dfrac{n}{8}\) 个节点需要下沉 \(2\) 层。共下沉 \(2 \times \dfrac{n}{8}\) 次。
- 倒数第 \(4\) 层的 \(\dfrac{n}{16}\) 个节点需要下沉 \(3\) 层。共下沉 \(3 \times \dfrac{n}{16}\) 次。
- \(\dots\)
那么最坏情况下所有元素的总移动次数为 \(S=0 \times \dfrac{n}{2} + 1 \times \dfrac{n}{4} + 2 \times \dfrac{n}{8} + 3 \times \dfrac{n}{16} + \dots\)。
显然,这是一个等差数列与等比数列逐项相乘后求和的问题,我们可以让其两边同时乘公比(这里为 \(\dfrac{n}{2}:\dfrac{n}{4}=\dfrac{n}{4}:\dfrac{n}{8}=\dots=2:1\),即为 \(2\)),然后与原式子错位相减。
故最坏时间复杂度为 \(\mathcal{O}(n)\)。
void build(int *_a,int n){
memcpy(a+1,_a,sizeof(int)*n); // 将传入数组拷贝到堆数组
l=n; // 记录现在堆的长度
for(int i=n>>1; i; i--) // 从 n/2 开始自底向上下沉
sink(i);
}
插入
- 将一个元素 \(x\) 插入到堆中。
可以直接把 \(x\) 插入到堆的尾部,然后对 \(x\) 进行一次上浮。
void push(int x){
a[++l]=x;
swim(l);
}
时间复杂度 \(\mathcal{O}(\log n)\)。
删除
- 删除堆中最小(大根堆中为最大)的元素。
使最后一个元素与堆顶元素交换,然后对堆顶元素进行下沉操作即可。
void pop(){
a[1]=a[l--];
sink(1);
}
查询
- 询问所有元素中最小(或最大)的元素。
直接返回根节点即可。
int top(){return a[1];}
P3378 【模板】堆
题面大意
给定一个序列,初始为空,需要支持三种操作:
- 将一个数 \(x\) 加入序列。
- 输出序列中最小的数。
- 删除序列中最小的数(若有多个,只删一个)。
思路
使用小根堆,只需要 push,pop,top 三种操作即可。
我写了一个堆的 class,支持任何类型,只需要在构造函数中传入一个用于比对元素的函数即可。若需要加入堆中的类型为结构体或类,可以直接在结构体或类中重载运算符 <,就不用传入比较函数了。
这个比较函数和 sort 函数的 cmp 类似,可以直接传函数、lambda 表达式、仿函数等。
要指定类型的话,在定义一个堆的时候这样写:
Head<type> a;
其中的 type 即为你所需的类型,若不指定,即为 int,可以直接省略 <type>。
若要指定比较函数,这样写:
Heap<type> a(1e6,->bool{return ...;})
第一个参数是堆最多可以达到的元素个数,传 \(10^6\) 一般没什么问题,第二个我这里写了一个 lambda 表达式,可以替换为你写好的函数名称(规则和 sort 一样)或仿函数(greater<type>() 之类的)。
代码
#include <iostream>
#include <cstring>
using namespace std;
template<typename T=int>
inline T read(){
T X=0; bool flag=1; char ch=getchar();
while(ch<'0' || ch>'9'){if(ch=='-') flag=0; ch=getchar();}
while(ch>='0' && ch<='9') X=(X<<1)+(X<<3)+ch-'0',ch=getchar();
if(flag) return X;
return ~(X-1);
}
template<typename T=int>
inline void write(T X){
if(X<0) putchar('-'),X=~(X-1);
T s[20],size=0;
while(X) s[++size]=X%10,X/=10;
if(!size) s[++size]=0;
while(size) putchar(s[size--]+'0');
putchar('\n');
}
const int N=1e6+5;
int n;
template<class T=int>
class Heap{
public:
Heap(int n=1e6,bool (*_cmp)(T,T)=[](T a,T b)->bool{return a<b;}):
a(new T[n+5]),l(0),cmp(_cmp){memset(a,0,sizeof(a));}
~Heap(){delete[] a;} // 构造函数和析构函数
void build(T *_a,int n){
memcpy(a+1,_a,sizeof(int)*n);
l=n;
for(int i=n>>1; i; i--)
sink(i);
}
void push(T x){
a[++l]=x;
swim(l);
}
void pop(){
a[1]=a[l--];
sink(1);
}
T top(){return a[1];}
bool empty(){return l==0;} // 判断是否为空
int size(){return l;} // 获取元素个数
private:
T *a; // 存储堆的数组
int l; // 元素个数
bool (*cmp)(T,T); // 不用管它,用来存储比较函数,想了解的话可以自行百度 “函数指针”
void swim(int x){ // 上浮
for(int i=x; i>1 && cmp(a[i],a[i>>1]); i>>=1)
swap(a[i],a[i>>1]);
}
void sink(int x){ // 下沉
for(int i=x,t=son(i); t<=l && cmp(a[t],a[i]); i=t,t=son(i))
swap(a[i],a[t]);
}
inline int ls(int x){return x<<1;}
inline int rs(int x){return x<<1|1;} // 分别获取左儿子和右儿子
// 获取较小的儿子(对于小根堆而言)
inline int son(int x){return ls(x)+(rs(x)<=l && cmp(a[rs(x)],a[ls(x)]));}
};
Heap h;
int main(){
n=read();
while(n--)
switch(read()){
case 1: h.push(read()); break;
case 2: write(h.top()); break;
case 3: h.pop(); break;
default: break;
}
return 0;
}
P1628 合并序列
题目大意
给定 \(n\) 个单词和一个字符串 \(T\),按照字典序从小到大输出以 \(T\) 为前缀的所有单词。
思路
因为要按照字典序排序,直接用一个字符串 string 类型的堆。
将输入的单词都 push 进去,不用动比较函数,因为本来就要按照字典序,直接用小于号也就是按字典序比较。
然后取 \(n\) 次堆顶元素,并删除。对于每个堆顶元素,先判断长度有没有 \(T\) 长,如果有,那么遍历字符串 \(T\),看看 \(T\) 是不是这个单词的前缀。是的话就输出。
代码
#include <iostream>
#include <cstring>
using namespace std;
int n,cnt;
string s,x;
template<class T=int>
class Heap{
public:
Heap(int n=1e6,bool (*_cmp)(T,T)=[](T a,T b)->bool{return a<b;}):
a(new T[n+5]),l(0),cmp(_cmp){memset(a,0,sizeof(a));}
~Heap(){delete[] a;}
void build(T *_a,int n){
memcpy(a+1,_a,sizeof(int)*n);
l=n;
for(int i=n>>1; i; i--)
sink(i);
}
void push(T x){
a[++l]=x;
swim(l);
}
void pop(){
a[1]=a[l--];
sink(1);
}
T top(){return a[1];}
bool empty(){return l==0;}
int size(){return l;}
private:
T *a;
int l;
bool (*cmp)(T,T);
void swim(int x){
for(int i=x; i>1 && cmp(a[i],a[i>>1]); i>>=1)
swap(a[i],a[i>>1]);
}
void sink(int x){
for(int i=x,t=son(i); t<=l && cmp(a[t],a[i]); i=t,t=son(i))
swap(a[i],a[t]);
}
inline int ls(int x){return x<<1;}
inline int rs(int x){return x<<1|1;}
inline int son(int x){return ls(x)+(rs(x)<=l && cmp(a[rs(x)],a[ls(x)]));}
};
Heap<string> h;
int main(){
scanf("%d",&n);
for(int i=1; i<=n; i++){
cin >> s;
h.push(s);
}
cin >> s;
for(int i=1; i<=n; i++,cnt=0){ // 别忘了将 cnt 置为 0
x=h.top();
h.pop();
// 当前字符串的长度连前缀串的长度都达不到,就可以跳过了
if(x.size()<s.size()) continue;
for(int i=0; i<s.size(); i++)
if(s[i]==x[i]) // 依次判断
cnt++; // 若相等,匹配字符数量+1
if(cnt==s.size()) // 很暴力的方法(
printf("%s\n",x.c_str());
}
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号