『学习笔记』省选 - 进阶线段树

有时咱们需要维护好大一个区间。这时按照上面的方法存储压力就有点大了。这里可以使用动态开点线段树：即不再使用编号乘 \(2\) (\(+1\)) 来编号左右儿子，而将左右儿子编号存储在节点内，初始为空，需要的时候再开一个新的结点。

另一些场景需要维护桶之类的东西。这时需要权值线段树。它通常用来查询序列中有多少个数落在给定区间内。（可以搭配离散化食用）

标记永久化：当懒标记的合并具有交换律，即合并结果与先后顺序无关，则可以标记永久化，不下传标记，而查询时将标记计入答案即可。例如，区间加查询区间和是可以的，而区间赋值查询区间和、矩阵乘法等不行。

空间问题：普通建树方式时，最大可能达四倍。动态开点时最大编号不超过 \(\ge n\) 的第一个 \(2\) 的整数幂的 \(2\) 倍。

例 - 所有子区间异或和的总和

单点修改，区间查询所有子区间的异或和的总和。数据 \(10^5\)。

见异或和的和，于是拆位分别维护。这样一来只需要维护 \(0,1\) 序列了。

对于一个结点，需要维护所有子区间异或和总和即所有异或和为 \(1\) 的子区间的个数。需要考虑跨越中点的异或和为 \(1\) 的区间数量，容易想到可以尝试再维护前后缀 \(0,1\) 来求（前后缀 \(1\) 可以通过长度减去前后缀 \(0\) 求得，所以可以仅维护前后缀 \(0\)）。而维护前后缀 \(0,1\) 则还需要维护整个区间的异或和。一共需要维护四样东西。查询时按位加起来即可。

P4198 楼房重建

转化斜率后，考虑维护每个区间从左边开始能看到的楼房个数，即左边开始最长严格递增子序列长度。

对于合并，显然左区间答案可以直接累加，然后考虑右区间，用左区间的最大值分别与右区间的左右区间最大值比较，递归下去累加右区间答案。

记录详情。

P7453 [THUSCH2017] 大魔法师

线段树+矩阵乘法。没什么好说的，难度都在实现上。

卡常技巧：快读，矩阵乘法循环展开，仅计算过程转 ll，仅加法时不使用 % 代而判断并作减法。

踩坑记录：build 中写了个 mid=l+r<<1；pushdown 未清空父节点懒标记。

记录详情。

P7576 「PMOI-3」期望乘积

挖个坑...

可持久化线段树

你需要维护这样的一个长度为 $ N $ 的数组，支持如下几种操作

1. 在某个历史版本上修改某一个位置上的值

2. 访问某个历史版本上的某一位置的值

涉及“历史版本”则需要使用可持久化线段树（即主席树）。

对于历史版本的存储，显然不可能每个版本都重新建立一棵树。那么可以考虑重复利用。对于每次修改，我们仅需克隆需要变动的结点，然后连向原树的结点即可。那么 \(n\) 个版本就会有 \(n\) 个根节点，可以开一个数组 root[i] 存储每个历史版本的根结点编号。

如图辅助理解（From)

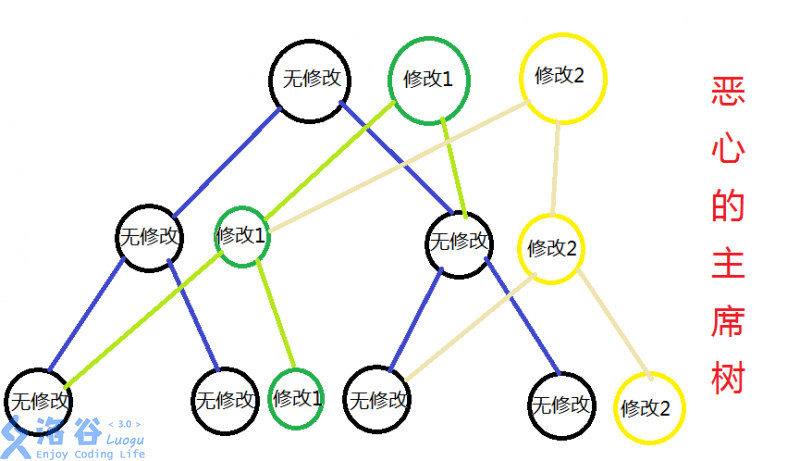
模板 1 的代码。

典例 - 静态区间第 \(k\) 小

题链。

即无修改操作，仅含 \(m\) 次查询操作：\([l,r]\) 内的第 \(k\) 小值。

乍一看：似乎和时间没什么关系啊......

这里要注意灵活运用了：主席树的时间维度也可以看作其他维度。就是说，假如线段树维护一条线，那么主席树可以维护一个平面。

观察到第 \(k\) 小值，发现可以离散化然后按值域维护桶建立主席树，这样第一维度就是值域，对于维护第 \(k\) 小值看起来会比较方便。

第二维度呢？考虑将 \(a_i\) 从 \(1\) 到 \(n\) 分别加入主席树，将 \(i\) 作为第二个维度。这样，在第 \(i\) 个“版本”中，很容易取得 \(a[1...i]\) 中第 \(k\) 小的值。

诶，有股前缀和的味？考虑拿第 \(r\) 个“版本”与第 \(l-1\) 个“版本”做差，这样可以得到 \([l,r]\) 中每个数出现个数，并且它具有单调性。于是就可以在做差得到的树上二分 \(k\) 啦！

代码。

码题经验：一定要记得把动态开点编号赋值好！

还有几道题...

TODU