洛谷P3478 [POI2008]STA-Station 题解
本题的数据是 n <= 1000000 , 应该是O(n) 算法;
先考虑最朴素的算法 , 进行n 次的dfs 求出深度和 , 复杂度是O(n ^2);
如果我们能在第一次dfs的基础上在对其他点的进行O(1)的求解那就满足复杂度的要求了;
然后我们画一下图(我不太会画图就不画了);
假设我们已经知道了 以x为根的答案 , 然后求出它的子节点y的答案;
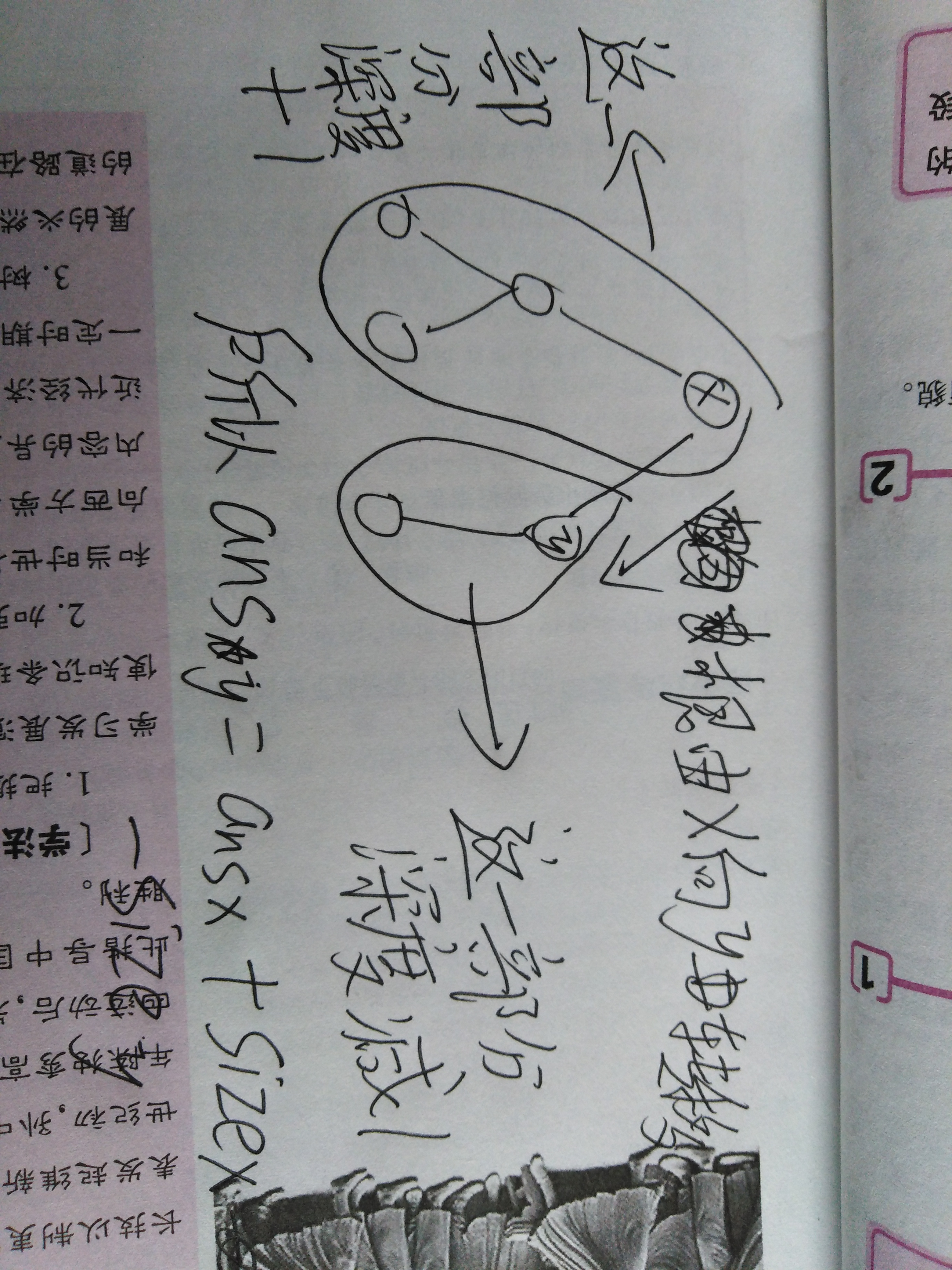
然后我们将根往y 移动 , 发现 原先以x为根的子树中 , 除去以y为根的子树 , 他们的深度都会加一 , 而 原先y的子树的所有节点都会减去1
所以答案asn_y = ans_x + size_x - size_y; (如下图)
这里附上我的代码
#include<cstdio> #include<queue> #include<map> #include<cstring> #include<cstdlib> #include<deque> #include<iostream> #include<vector> #include<algorithm> #define inf 0x3f3f3f3f #define M 1000010 using namespace std; int cnt , head[M] , next[M << 1] , u[M << 1] , n , ans, size[M]; long long d[M] , f[M] , maxn ; void add(int x , int y){ u[++cnt] = y , next[cnt] = head[x] , head[x] = cnt; } inline void dfs1(int x , int fa , int dep){ int y ; for (int i = head[x] ; i ; i = next[i]){ y = u[i]; if ( y == fa) continue; dfs1(y , x , dep + 1); size[x] += size[y] , d[x] += d[y]; } size[x] += 1 , d[x] += dep; } inline void dfs2(int x , int fa){ int y; for (int i = head[x] ; i ; i = next[i]){ y = u[i]; if (y == fa) continue; f[y] = f[x] + n - size[y] * 2; dfs2(y , x); } } int main(){ // freopen("A.out" , "w" , stdout); // freopen("c1.in" , "r" , stdin); scanf("%d" , &n); for (int i = 1 ; i < n ; ++i){ int a , b; scanf("%d%d" , &a , &b); add(a , b); add(b , a); } dfs1(1 , 0 , 0); f[1] = d[1]; dfs2(1 , 0 ); for (int i = 1 ; i <= n ; ++i) if (f[i] > maxn) ans = i , maxn = f[i]; printf ("%d" , ans); return 0; }
注意要把存深度的数组开longlong


