20172328 2018-2019《Java软件结构与数据结构》第九周学习总结

20172328 2018-2019《Java软件结构与数据结构》第九周学习总结

概述 Generalization

本周学习了无向图、有向图、带权图、常用的图算法、图的实现策略。

教材学习内容总结 A summary of textbook

  • 图（graph）

  • 与树类似，图由结点和这些结点之间的连接构成。

    • 对有n个结点的无向图，要使该图是完全的，要求有n（n-1）/ 2个边。
    • 对有n个结点的有向图，要使该图是完全的，要求有n（n-1）个边。

  • 无向图（undirected graph）

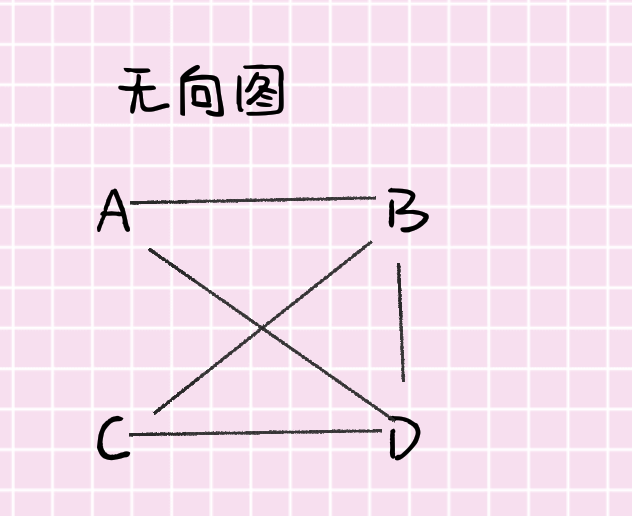
  • 无向图是一种边为无序结点对的图。

    • 无序结点（undirected vertice）：A、B、C、D
    • 边（edge）（注：由于无序，所以<a,b>和<b,a>一样）：(A,B) (B,D) (A,D) (B,C) (C,D)
    • 邻接（adjacent）：如果图中两个顶点之间有一条连通边，则称这两个顶点是邻接的。如图，A和B邻接，A和C不邻接。
    • 自循环（self-loop）或环（sling）：连通一个顶点及其自身的边称为自循环，如图，边（A,A）表示是A连接自身的一个环。
    • 连通（connected）：如果无向图中的任意两个顶点之间都存在一条路径，则认为这个无向图连通。
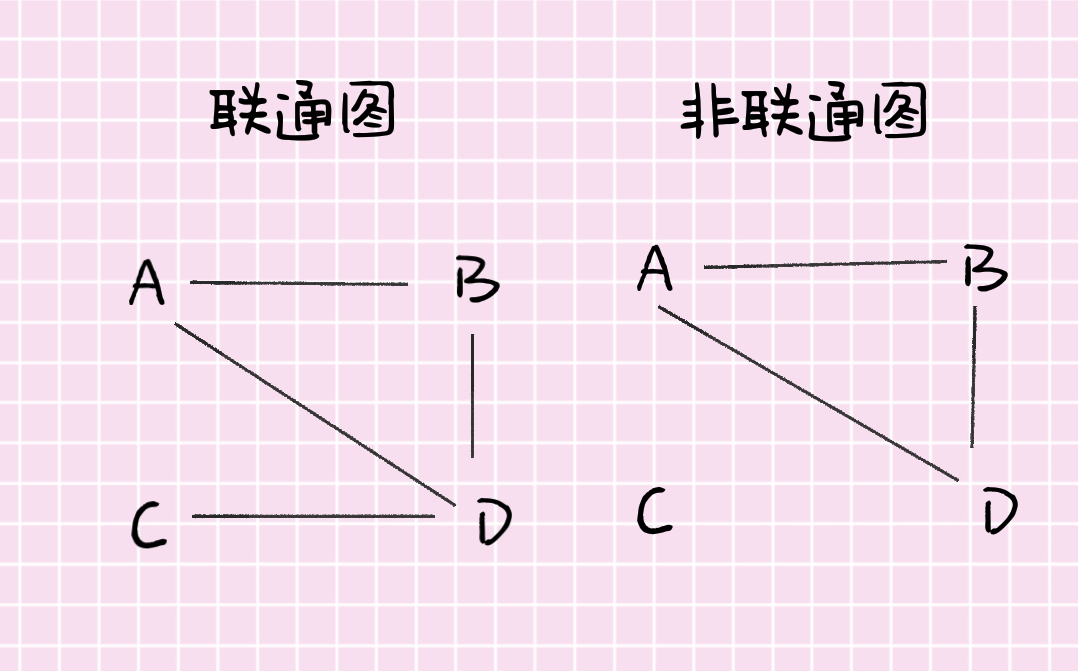
    • 无向树是一种连通的无环无向图，其中一个元素被指定为树根。

  • 有向图（directed graph）

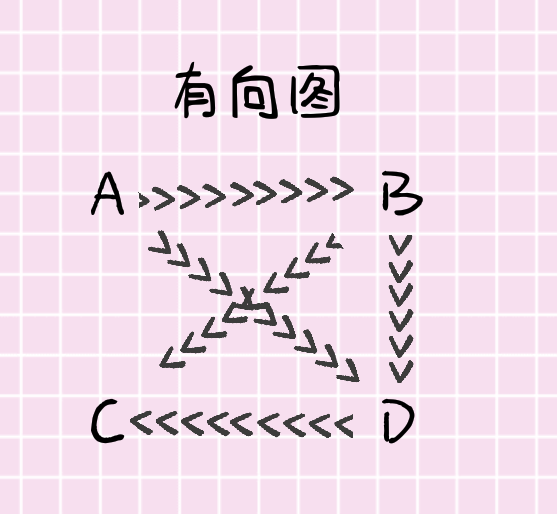
  • 边为有序顶点对的图。也称为双向图（digraph）。

    • 有序结点（directed vertice）：A、B、C、D
    • 边（edge）（注：由于有序，所以<a,b>和<b,a>不同）：(A,B) (B,D) (A,D) (B,C) (D,C)
    • 连通（connected）：如果有向图中的任意两个顶点之间都存在一条路径且能通过一些路径遍历到所有的顶点，则认为这个有向图连通。
    • 拓扑序（topological order）：如果有向图中没有环路，且有一条从A到B的边，则可以把顶点A安排到顶点B之前，这种排列得到的顶点次序称为拓扑序。

  • 网络（network）

  • 有向网络

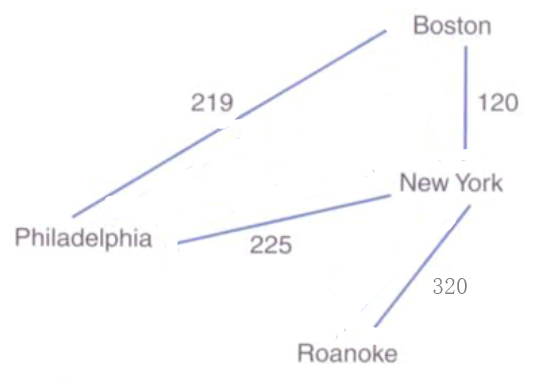
  • 无向网络

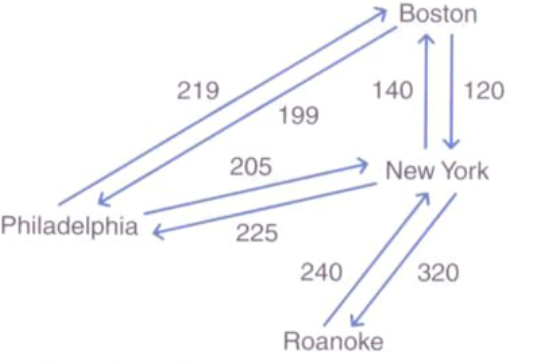
  • 网络（带权图）：每条边都对应一个权值（数据信息）的图。（例如：城市之间的航线票价）

    • 对于网络，我们用三元数组来表示每条边。这个三元数组中包括起始顶点、终止顶点和权重。
    • 如上图，我们就可以表示为： （Boston ，New York ，120）、（Boston ，Philadeiphia ， 199）等

  • 常用的图算法 ：

  • 图的遍历：

    • 广度优先遍历：从一个顶点开始，辐射状地优先遍历其周围较广的区域。就如同树中的层次遍历。
    • 深度优先遍历：图的深度优先搜索，类似于树的先序遍历，所遵循的搜索策略是尽可能“深”地搜索图。就如同树中的前序遍历。

  • 测试连通性：

    • 连通性：图中的任意两个顶点之间都存在一条路径，则认为这个图是连通的。
    • 测试方法：
      • 从任意结点开始的广度优先遍历中得到的顶点数等于图中所含顶点数。

  • 生成树（spanning tree）：包含图中所有顶点及图中部分边的一棵树。

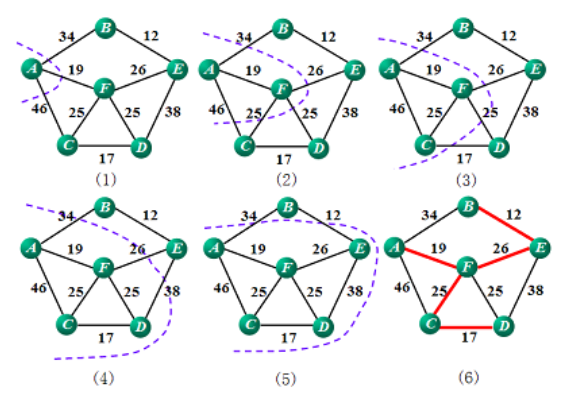
  • 最小生成树（minimum spanning tree）:所含边权值之和小于其他生成树的边的权值之和。

  • 判定最短路径：

① 判定起始顶点和目标顶点之间是否存在最短路径（两个顶点之间边数最少的路径）。
② 在加权图中找到最短路径。（Dijkstra算法）

  • 图的实现策略：

  • 邻接列表：用一种类似于链表的动态结点来存储每个结点带有的边。这种链表称为邻接列表。

  • 邻接矩阵：用一种叫邻接矩阵的二维数组来表示任意两个顶点的交接情况。

  • 无向图的邻接矩阵一定是对称的，有向图的邻接矩阵不一定对称。

教材学习中的问题和解决过程 Problem and countermeasure

  • 问题1：在看课本的时候，对拓扑序没有认识清楚。
  • “拓扑序（topological order）：如果有向图中没有环路，且有一条从A到B的边，则可以把顶点A安排到顶点B之前，这种排列得到的顶点次序称为拓扑序。”
  • 问题1的解决：在看了相关资料并进行了理解分析后进行如下总结。
  • 首先先介绍两个概念：
    • 入度：有序图中指向该结点的边的总数。
    • 出度：有序图中该结点指向其他结点的边的总数。
  • 拓扑排序，其实就是寻找一个入度为0的顶点，该顶点是拓扑排序中的第一个顶点序列，将之标记删除，然后将与该顶点相邻接的顶点的入度减1，再继续寻找入度为0的顶点，直至所有的顶点都已经标记删除或者图中有环。

从上可以看出，关键是寻找入度为0的顶点。

一种方式是遍历整个图中的顶点，找出入度为0的顶点，然后标记删除该顶点，更新相关顶点的入度，由于图中有n个顶点，每次找出入度为0的顶点后会更新相关顶点的入度，因此下一次又要重新扫描图中所有的顶点。故时间复杂度为O(n^2)。

  • 问题2：我一直以为pp15.1是补全graph代码即可，后来才知道是要用邻接列表来实现。邻接列表究竟是什么？书上草草解释不能让我全懂，自然不能顺利的完成作业。
  • 问题2的解决：
  • 邻接表，其实是一个顶点表，每个顶点又拥有一个边列表。下图是图的邻接表表示:

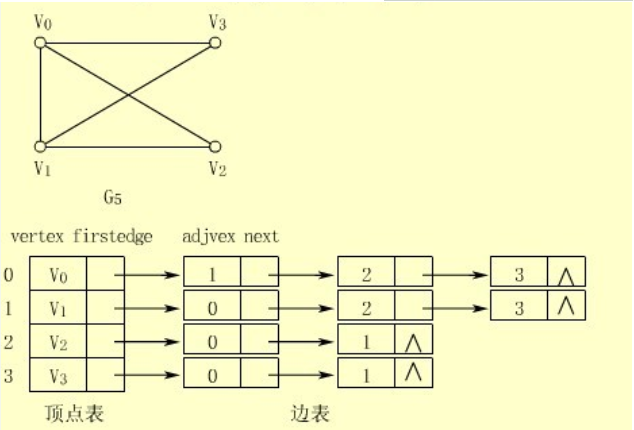
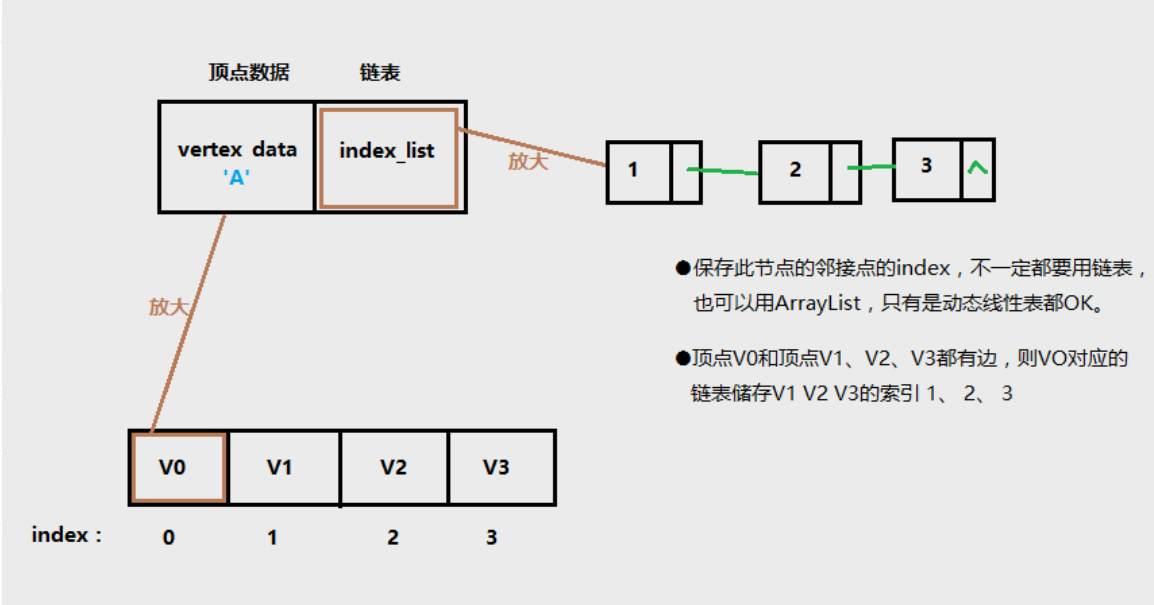
  • 从图中可以看出，图的实现需要能够表示顶点表，能够表示边表。邻接表指是的哪部分呢？每个顶点都有一个邻接表，一个指定顶点的邻接表中，起始顶点表示边的起点，其他顶点表示边的终点。
  • 邻接表的处理方法是这样的。

1、图中顶点用一个一维数组存储，另外，对于顶点数组中，每个数据元素还需要存储指向第一个邻接点的指针，以便于查找该顶点的边信息。

2、图中每个顶点vi的所有邻接点构成一个线性表，由于邻接点的个数不定，所以用单链表存储，无向图称为顶点vi的边表，有向图称为顶点vi作为弧尾的出边表。

代码实现时的问题作答 Exercise

  • 问题1：在编写无向网络时需要写一个最便宜路径的问题，当时没有想出来怎么去写，找了一下书上关于这个问题的描述，是关于用Dijkstra算法来解决的。那么，Dijkstra算法具体如何解决问题？
  • 问题1的解决：
  • 选了一篇我认为介绍的最清楚的博客

(1) 初始时，S只包含起点s；U包含除s外的其他顶点，且U中顶点的距离为"起点s到该顶点的距离"[例如，U中顶点v的距离为(s,v)的长度，然后s和v不相邻，则v的距离为∞]。
(2) 从U中选出"距离最短的顶点k"，并将顶点k加入到S中；同时，从U中移除顶点k。
(3) 更新U中各个顶点到起点s的距离。之所以更新U中顶点的距离，是由于上一步中确定了k是求出最短路径的顶点，从而可以利用k来更新其它顶点的距离；例如，(s,v)的距离可能大于(s,k)+(k,v)的距离。
(4) 重复步骤(2)和(3)，直到遍历完所有顶点。



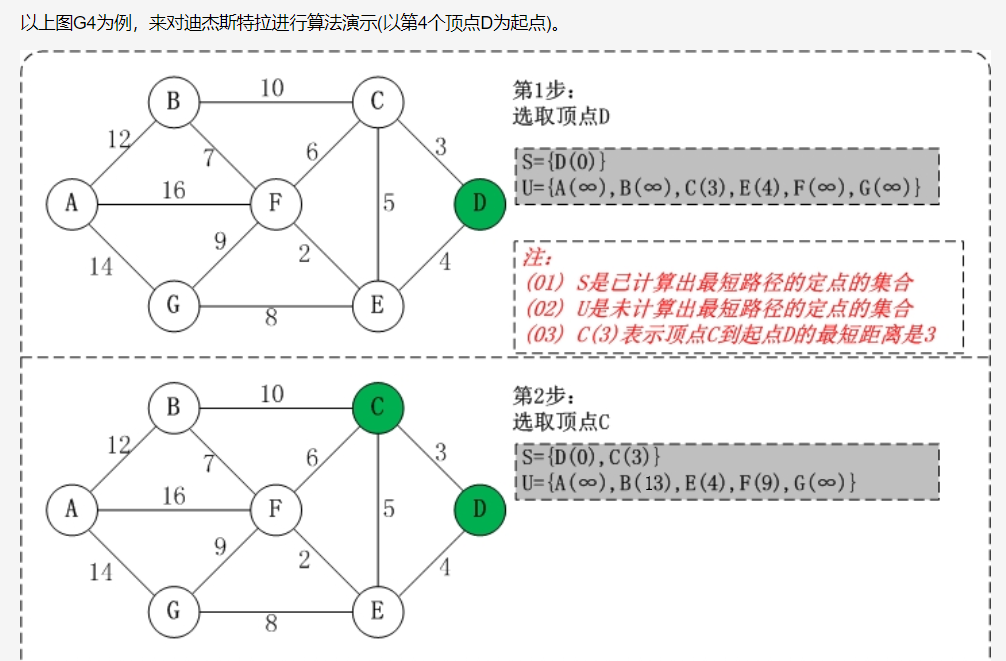
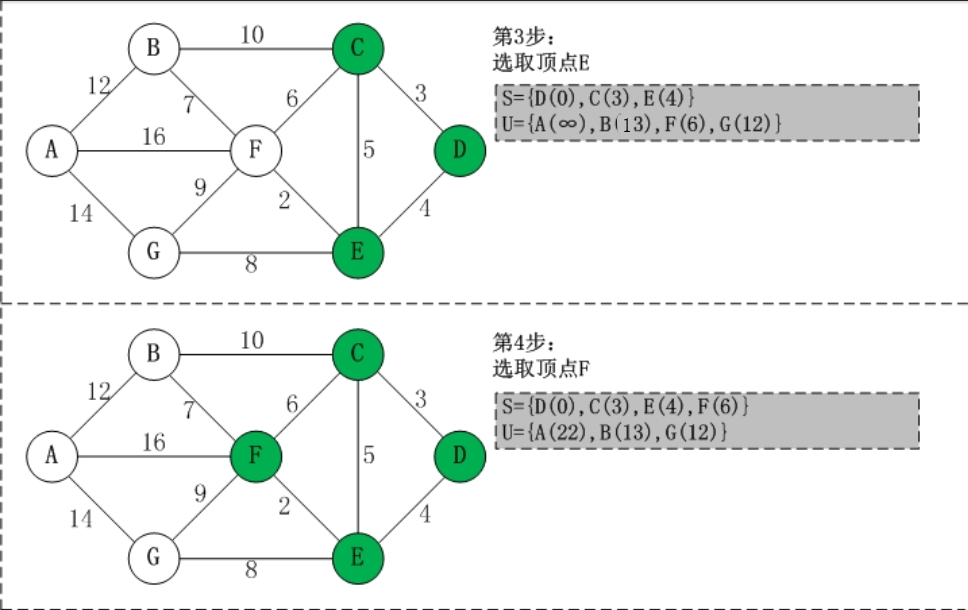
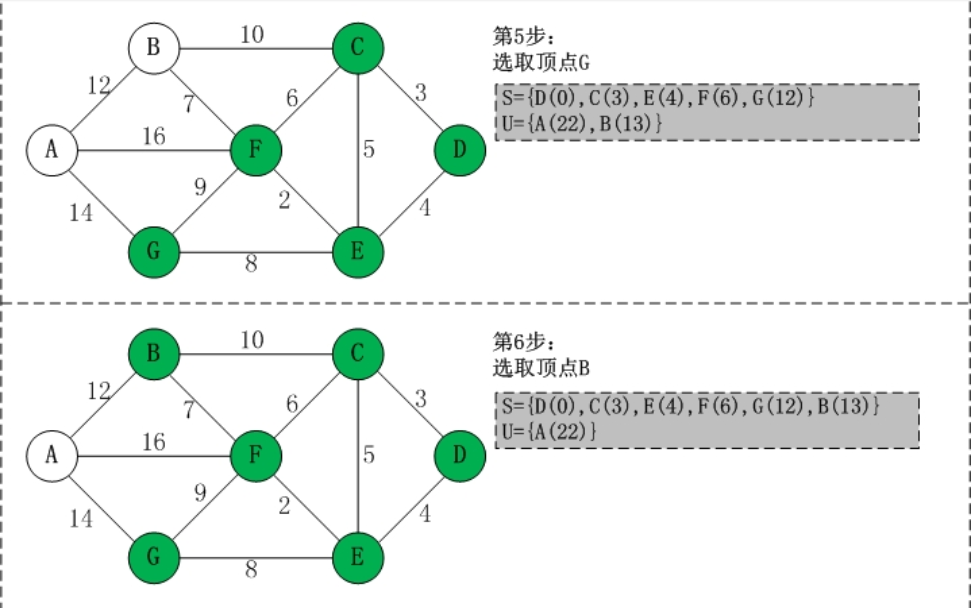
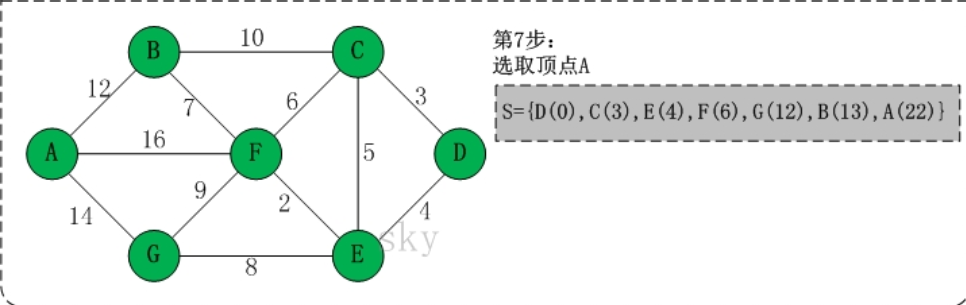
通过理解及其博客里面的代码讲解，就可以明白该算法的奥妙啦。

  • 问题2：在做pp15.1的时候出现了越界的问题。

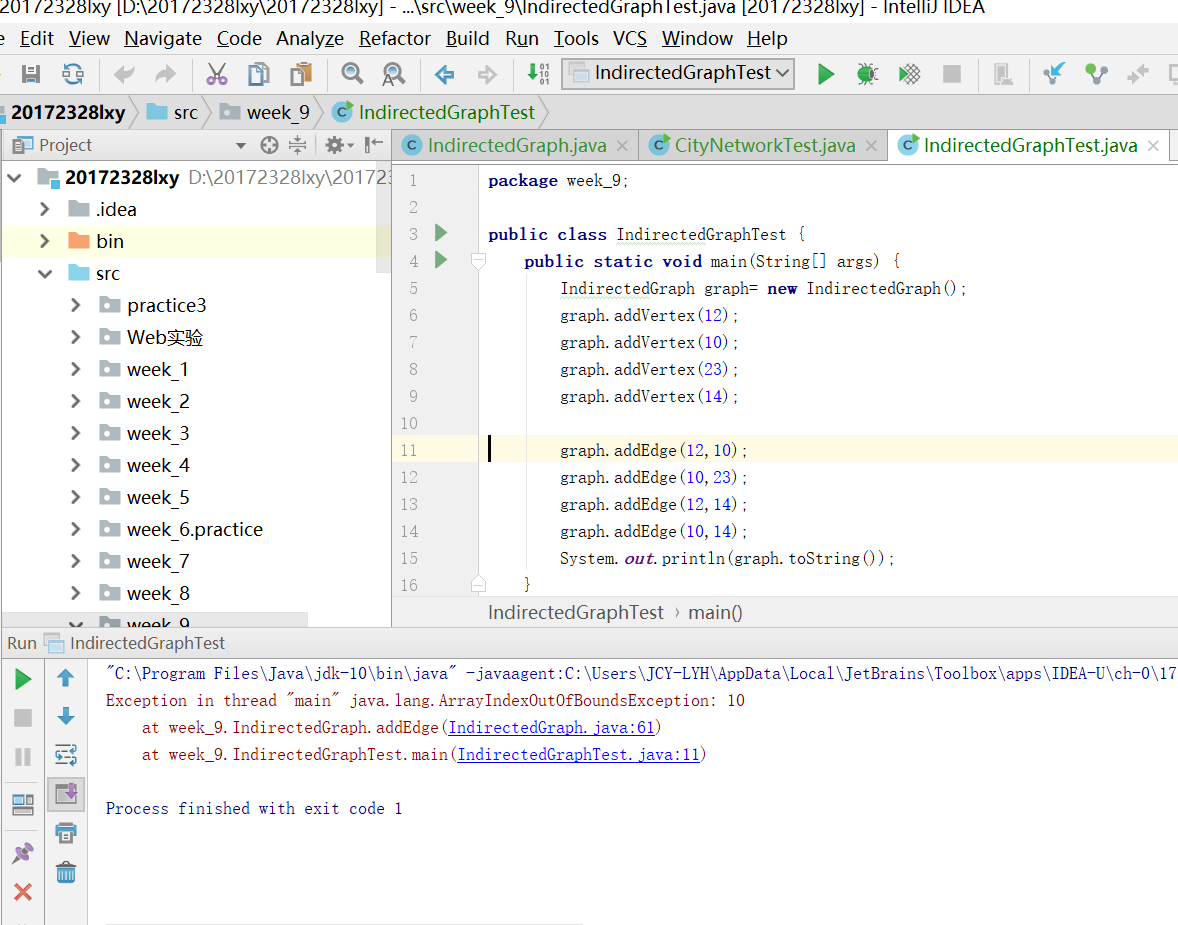
  • 问题2的解决：正在改正····

上周测试活动错题改正 Correction

  • 问题1：Since a heap is a binary search tree, there is only one correct location for the insertion of a new node, and that is either the next open position from the left at level h or the first position on the left at level h+1 if level h is full.
    A .True
    B .Flase √
  • 问题1的改正：本题应该是错误的,选B。堆是一个完全二叉树而不是一个二叉查找树，太低级的错误了，完全粗心所致。

码云链接

代码量（截图）

结对及互评Group Estimate

点评模板：

  • 博客中值得学习的或问题：
    • 20172301：偏序和全序我们在离散课上还没学到，但是你已经把拓扑排序和快速排序以及离散内容联系起来了，୧(๑•̀◡•́๑)૭ Amazing！
    • 20172304：博客真的进步很大呀！图片如果小一点就太好啦。代码错题解答可以再详细一点。继续加油！

其他（感悟、思考等，可选）Else

图这一章很有趣。很多算法实现很新颖，需要好好理解消化。 还有代码实现确实很费时间呀（绕来绕去绕不过来）
正在继续告诉自己，请对专业课更加虔诚一点。

学习进度条Learning List

代码行数（新增/累积） 博客量（新增/累积） 学习时间（新增/累积）
目标 5000行 30篇 400小时
第一周 0/0 1/1 8/8
第二周 621/621 1/2 12/20
第三周 678/1299 1/3 10/30
第四周 2734/4033 1/4 20/50
第五周 1100/5133 1/5 20/70
第六周 1574/6707 2/7 15/85
第七周 1803/8510 1/8 20/105
第八周 2855/11365 2/10 25/130
第九周 2076/13441 1/11 25/155

参考资料Reference

posted @ 2018-11-18 08:54  虹澄清晓  阅读(346)  评论(1)  编辑  收藏  举报
页尾